6.3万有引力定律 提高

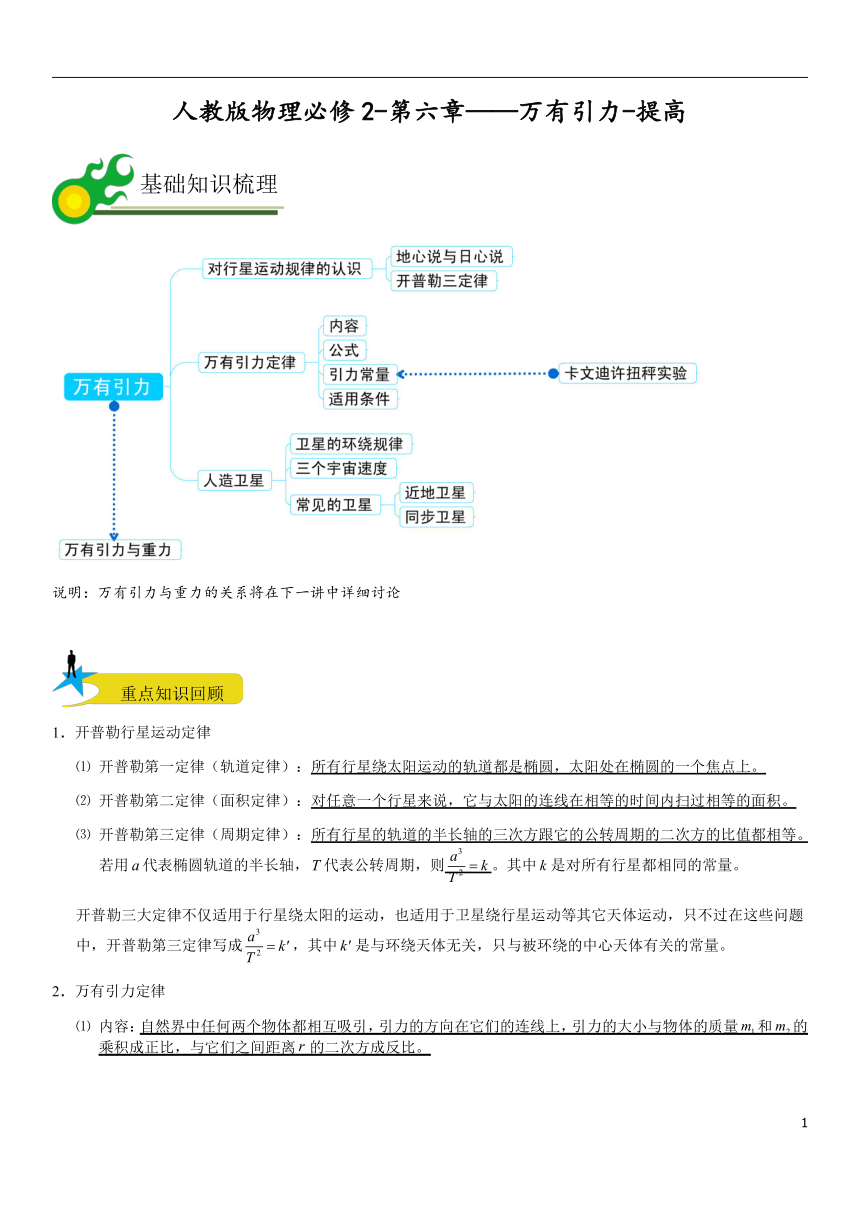
人教版物理必修2-第六章——万有引力-提高

(
基础知识梳理
)

说明：万有引力与重力的关系将在下一讲中详细讨论

(
重点知识回顾
)
1．开普勒行星运动定律
⑴ 开普勒第一定律（轨道定律）：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上。
⑵ 开普勒第二定律（面积定律）：对任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积。
⑶ 开普勒第三定律（周期定律）：所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。若用代表椭圆轨道的半长轴，代表公转周期，则。其中是对所有行星都相同的常量。
开普勒三大定律不仅适用于行星绕太阳的运动，也适用于卫星绕行星运动等其它天体运动，只不过在这些问题中，开普勒第三定律写成，其中是与环绕天体无关，只与被环绕的中心天体有关的常量。
2．万有引力定律
⑴ 内容：自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量和的乘积成正比，与它们之间距离的二次方成反比。
⑵ 公式：，是比例系数，叫做引力常量，适用于任何两个物体，通常取。值由卡文迪许首先精确测出。
⑶ 万有引力定律的适用条件
① 当两个物体间的距离远远大于每个物体的尺寸时，物体可以看成质点，它们之间的引力可直接使用万有引力定律公式计算。
② 通过严格的理论分析得到，质量分布均匀的球体，它们之间的引力也可直接使用公式计算，这时是两球心间的距离。
3．三种宇宙速度
⑴ 第一宇宙速度（环绕速度）：；
第一宇宙速度是使卫星能环绕地球运行所需的最小发射速度。
⑵ 第二宇宙速度（脱离速度）：；
在地面附近发射人造卫星，如果发射速度大于，而小于，那么它绕地球运行的轨迹将是椭圆。当发射速度等于或大于时，卫星会克服地球的引力而永远离开地球。
⑵ 第三宇宙速度（逃逸速度）：。
当卫星的发射速度等于或大于时，卫星将挣脱太阳引力的束缚，飞到太阳系外。
4．同步卫星与近地卫星
⑴ 同步卫星
地球同步卫星是人为发射的一种卫星，它相对于地球静止于赤道上空。从地面上看，卫星保持不动，故也称静止卫星，从地球之外看，卫星角速度（或周期）与地球自转角速度（或周期）相同，故称地球同步卫星。
⑵ 近地卫星
近地卫星轨道半径较小，贴近地球表面，其轨道半径近似等于地球半径。
(
基础训练
)
如图所示为地球绕太阳运行的示意图，图中椭圆表示地球公转轨道，、、、分别表示中国农历节气中的春分、秋分、夏至、冬至时地球所在的位置。试分析为什么秋冬两季比春夏少几天？

地球绕太阳运行时，对北半球的观察者而言，在冬天经过近日点，夏天经过远日点，由开普勒第二定律可知，地球在冬天比在夏天运动得快一些，因此经过的时间比经过的时间长，即春夏两季比秋冬两季长一些。（或者从题图可以看出春分到秋分的春夏两季地日连线所扫过的面积比从秋分到次年春分的秋冬两季地日连线所扫过的面积大，再结合开普勒第二定律可以得出，春夏两季比秋冬两季长一些。）

木星的公转周期约为12年，如把地球到太阳的距离作为1天文单位，则木星到太阳的距离约为
A．2天文单位 B．4天文单位 C．5.2天文单位 D．12天文单位
C
关于引力常量，下列说法中正确的是
A．值的测出使万有引力定律有了真正的实用价值，可用万有引力定律进行定量计算
B．引力常量的大小与两物体质量乘积成反比，与两物体间距离的平方成正比
C．引力常量的物理意义是，两个质量是的物体相距时相互吸引力为
D．引力常量是不变的，其值大小与单位制的选择无关
AC
两个质量分布均匀且大小相同的实心小铁球紧靠在一起，它们之间的万有引力为，若两个半径是小铁球半径2倍的实心大铁球紧靠在一起，则它们之间的万有引力为
A． B． C． D．
D

(
2.1
万有引力的计算
)
(
知识点睛
)
万有引力定律公式只适用于两个质点间的作用，或是两个质量分布均匀的球体间的作用，若两个物体不是质点、也不是质量分布均匀的球体，可以采用对称或割补等方法解决。
(
例题精讲
)
设想把一个在地球表面重为10N的物体放到地球中心，这时物体受到地球对它的引力为
A．0 B．10N C．无穷大 D．无法求出
A

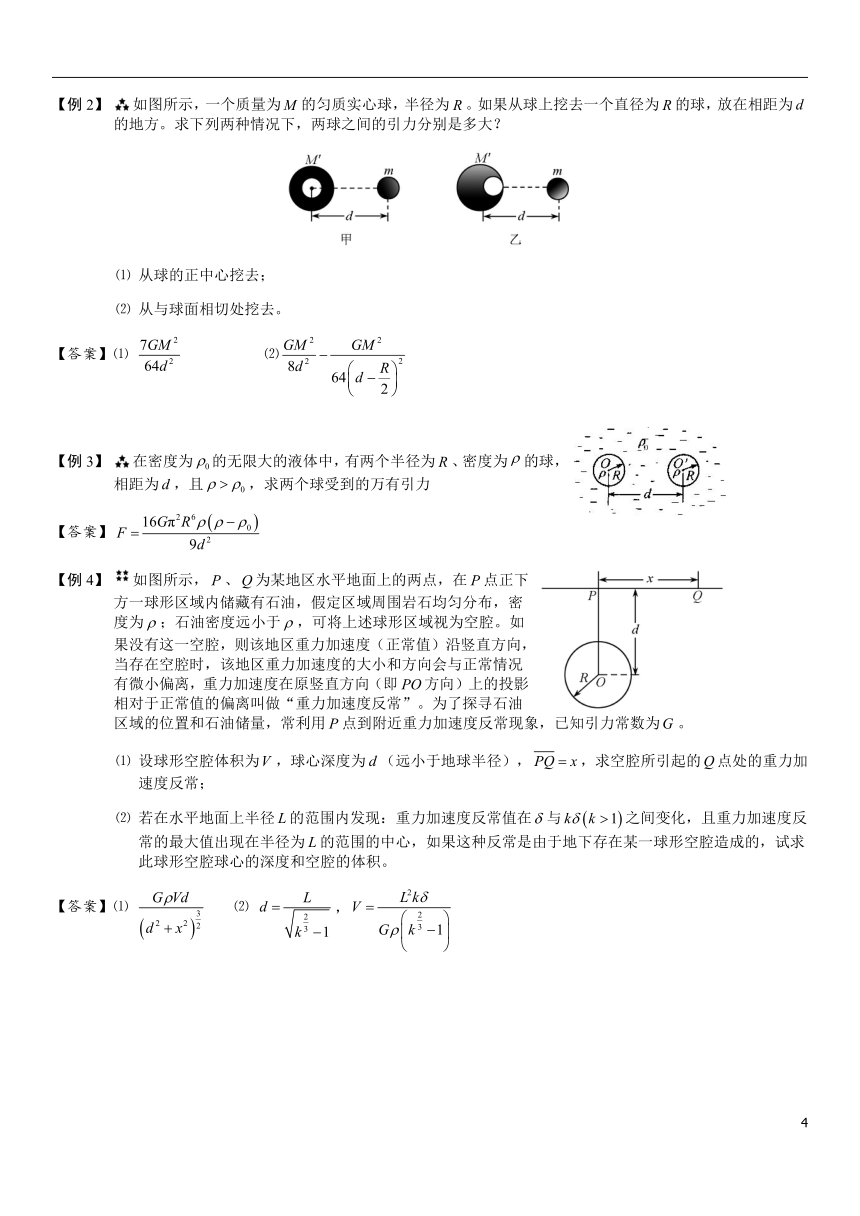
如图所示，一个质量为的匀质实心球，半径为。如果从球上挖去一个直径为的球，放在相距为的地方。求下列两种情况下，两球之间的引力分别是多大？

⑴ 从球的正中心挖去；
⑵ 从与球面相切处挖去。
⑴ ⑵

在密度为的无限大的液体中，有两个半径为、密度为的球，相距为，且，求两个球受到的万有引力

如图所示，、为某地区水平地面上的两点，在点正下方一球形区域内储藏有石油，假定区域周围岩石均匀分布，密度为；石油密度远小于，可将上述球形区域视为空腔。如果没有这一空腔，则该地区重力加速度（正常值）沿竖直方向，当存在空腔时，该地区重力加速度的大小和方向会与正常情况有微小偏离，重力加速度在原竖直方向（即方向）上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量，常利用点到附近重力加速度反常现象，已知引力常数为。
⑴ 设球形空腔体积为，球心深度为（远小于地球半径），，求空腔所引起的点处的重力加速度反常；
⑵ 若在水平地面上半径的范围内发现：重力加速度反常值在与之间变化，且重力加速度反常的最大值出现在半径为的范围的中心，如果这种反常是由于地下存在某一球形空腔造成的，试求此球形空腔球心的深度和空腔的体积。
⑴ ⑵ ，




(
2.2
天体的环绕规律
)
(
知识点睛
)
1．卫星的运行规律
在高中阶段，我们一般近似认为卫星的运动轨道为圆形，在运动过程中只受到万有引力的作用，这样万有引力提供了卫星做圆周运动的向心力。设卫星的轨道半径为、线速度大小为、角速度为、周期为、向心加速度为。
⑴ 线速度规律
由可得：，即线速度。
⑵ 角速度规律
由可得：，即角速度
⑶ 周期规律
由可得：，即周期
⑷ 向心加速度规律
由可得：，即向心加速度
⑸ 轨道平面规律
由于地球对卫星的万有引力方向指向地心，因此卫星做圆周运动的轨道平面必过地心。
综上所述，可知：
以上规律不仅适用于卫星环绕地球的运动，对其它星球的卫星及类似的环绕天体也适用。

(
注意区分半径与距离
万有引力公式
中的
指的是两个质点间的距离（对于两个均匀球体，是球心间的距离）；而向心力公式
中的
，对于圆轨道指的是圆半径； 当中心天体不动时，半径与距离相等，而在后面会碰到的双星等问题中，两者是不相等的，请大家注意区分。
)

2．第一宇宙速度的理解
⑴ 第一宇宙速度的推导
当物体以第一宇宙速度发射时，它将绕地球表面做匀速圆周运动，设地球质量为，绕地球做匀速圆周运动的卫星质量为，它到地心的距离为。卫星做圆周运动所需的向心力由万有引力提供，则有，解得。此时约等于地球半径，带入数据可解得：。
⑵ 发射速度与运行速度
① 在地面附近以某一速度发射一个物体，发射后不再对物体提供动力，被发射物体仅靠自己的初动能克服地球引力，进入运行轨道，这个在地面时的初速度称为发射速度，三个宇宙速度都是指发射速度。以第一宇宙速度发射的卫星，只能“贴着”地面运行，要使卫星进入离地面较高的轨道运行，就需要提供更大的发射速度。
② 运行速度是指卫星在进入运行轨道稳定飞行时，做匀速圆周运动的线速度，根据前面的推导，我们知道，可见轨道半径越大，运行速度越小。
(
请大家注意区分发射速度与运行速度。运行速度越大的卫星，对应的轨道半径越小，发射时的发射速度越小。
第一宇宙速度既是人造卫星的最小地面发射速度，又是人造卫星的最大环绕速度。
)
3．同步卫星、近地卫星、赤道上物体的比较
⑴ 同步卫星
寒假课程中我们已经学习了同步卫星的一些特点，这些特点可以被归纳为七个方面：
① 轨道一定
地球同步卫星绕地球旋转的轨道平面一定，与地球的赤道面重合。
② 运行方向一定
同步卫星运行时的转动方向与地球自转方向相同，即自西向东旋转。
③ 运行周期一定
同步卫星的运行周期与地球的自转周期相同
④ 角速度一定
由于，故同步卫星的角速度都相同（等于地球的自转角速度）
⑤ 距离地球表面的高度一定
由于万有引力提供向心力，，得，同步卫星运行的轨道半径。
注意：天体的半径和天体卫星的轨道半径不同，只有卫星贴近天体表面运动时，可近似认为轨道半径等于天体半径。计算时要区分天体半径、轨道半径、距离天体表面的高度几个量。
⑥ 向心加速度的大小一定
由，可得
⑦ 环绕速率一定
在轨道半径确定的条件下，同步卫星的环绕速率也确定，
⑵ 近地卫星
① 近地卫星其轨道半径近似等于地球半径
② 运行速度，即第一宇宙速度，是所有卫星中的最大绕行速度
③ 运行周期是所有卫星中的最小周期
④ 向心加速度，是所有卫星的最大加速度
⑶ 赤道上的物体
地球赤道上的物体随地球自转做圆周运动所需的向心力，由万有引力与地面支持力的合力提供；其运动的角速度、周期与地球自转的角速度、周期相同；线速度等于地球赤道处自转的线速度。
⑷ 同步卫星、近地卫星、赤道上的物体对比
① 同步卫星与近地卫星
相同点：都是人造卫星，由万有引力提供向心力，因此可以应用卫星的运行规律进行讨论；
不同点：同步卫星的轨道半径较大，由卫星的运行规律可知，它的周期较长、线速度、角速度、向心加速度较小。
② 赤道上的物体与同步卫星
相同点：都做匀速圆周运动，可以应用匀速圆周运动规律处理；角速度都等于地球自转角速度，周期都等于地球自转周期
不同点：Ｉ受力情况不同，赤道上的物体受万有引力和支持力作用，不能当做卫星处理。
Ⅱ轨道半径不同；根据圆周运动公式，可知，同步卫星的线速度、向心加速度均大于赤道上的物体。
③ 赤道上的物体与近地卫星
相同点：都做匀速圆周运动，可以应用匀速圆周运动规律处理；轨道半径相同
不同点：受力情况不同，赤道上的物体受万有引力和支持力作用，不能当做卫星处理，其向心加速度、线速度、角速度均小于近地卫星，周期长于近地卫星。
综上所述，在对比三者时，主要用到两类公式：卫星的运行规律和匀速圆周运动规律，其中赤道上的物体只遵守匀速圆周运动规律，而同步卫星和近地卫星同时遵守两类规律，因此，在比较②③时，主要应用的是匀速圆周运动的规律；在比较①时，主要应用的是卫星的运行规律。

(
例题精讲
)
已知，嫦娥二号探月卫星环月飞行的高度距离月球表面，所探测到的有关月球的数据比环月飞行高度为的嫦娥一号更加详实。若两颗卫星环月飞行均可视为匀速圆周运动，飞行轨道如图所示。则
A．嫦娥二号环月飞行的周期比嫦娥一号更小
B．嫦娥二号环月飞行的线速度比嫦娥一号更小
C．嫦娥二号环月飞行时角速度比嫦娥一号更小
D．嫦娥二号环月飞行时向心力加速度比嫦娥一号更小
A
木星有多颗卫星，其中是木卫一、木卫二的轨道都近似为圆。已知木卫一的周期为1.77天，木卫二的周期为3.55天，则两颗卫星相比
A．木卫一距木星表面较近 B．木卫二的角速度较大
C．木卫一的运动速度较大 D．木卫二的运动速度较大
AC
如图所示，、是两颗绕地球做匀速圆周运动的人造卫星，它们距地面的高度分别是和 (为地球半径)。下列说法中正确的是
A．、的线速度大小之比是
B．、的周期之比是
C．、的角速度大小之比是
D．、的向心加速度大小之比是
CD
关于地球的第一宇宙速度，下列说法正确的是
A．它是人造地球卫星绕地球飞行的最小速度
B．它是近地圆形轨道上人造地球卫星的运行速度
C．它是能使卫星进入近地圆形轨道的最小发射速度
D．与地球质量无关
BC
美国宇航局2011年12月5日宣布，他们发现了太阳系外第一颗类似地球的、可适合居住的行星——“开普勒-226”，其直径约为地球的2.4倍。至今其确切质量和表面成分仍不清楚，假设该行星的密度和地球相当，根据以上信息，估算该行星的第一宇宙速度等于
A． B．
C． D．
D
下面关于同步通信卫星的说法中不正确的是
A．同步通信卫星和地球自转同步，卫星的高度和速率都是确定的
B．同步通信卫星的角速度虽已被确定，但高度和速度率可以选择，高度增加，速率增大；高度降低，速率减小，仍同步
C．我国发射的第一颗人造地球卫星的周期是，比同步通信卫星的周期短，所以第一颗人造卫星离地面的高度比同步通信卫星低
D．同步通信卫星的速度比我国发射的第一颗人造卫星的速率小
B
中国正在实施北斗卫星导航系统建设工作，将相继发射五颗静止轨道卫星和三十颗非静止轨道卫星，到2020年左右，建成覆盖全球的北斗卫星导航系统。中国北斗卫星导航系统官方网站2010年1月22日发布消息说，五天前成功发射的中国北斗卫星导航系统第三颗组网卫星，经过四次变轨，于北京时间当天凌晨一时四十七分，成功定点于东经一百六十度的赤道上空。关于成功定点后的“北斗导航卫星”，下列说法正确的是
A．离地面高度一定，相对地面静止
B．运行速度大于7.9 km/s小于11.2km/s
C．绕地球运行的角速度比月球绕地球运行的角速度小
D．向心加速度与静止在赤道上物体的向心加速度大小相等
A
已知地球赤道上的物体随地球自转的线速度大小为、向心加速度大小为，近地卫星线速度大小为、向心加速度大小为，地球同步卫星线速度大小为、向心加速度大小为。设近地卫星距地面高度不计，同步卫星距地面约为地球半径的倍。则以下结论正确的是
A． B． C． D．
CD
如图所示，a为地球赤道上的物体，b为沿地球表面附近做匀速圆周运动的人造卫星，c为地球同步卫星。关于a、b、c做匀速圆周运动的说法中正确的是
A．角速度的大小关系为
B．向心加速度的大小关系为
C．线速度的大小关系为
D．周期关系为
D

根据观测，某行星外围有一模糊不清的圆环（如图，该圆环不在行星的同步卫星轨道高度上）。为了判断该圆环是连续物还是卫星群，已测出了环内各层的线速度的大小和该层至行星中心的距离，下列判断中正确的是

A．若与成正比，则圆环是连续物
B．若与成反比，则圆环是连续物
C．若与成正比，则圆环是卫星群
D．若与成反比，则圆环是卫星群
AD
2011年8月，嫦娥二号成功进入了环绕“日地拉格朗日点”的轨道，我国成为世界上第三个造访该点的国家。如图所示，该拉格朗日点位于太阳和地球连线的延长线上，一飞行器处于该点，在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动，则此飞行器的
A．线速度大于地球的线速度
B．向心加速度大于地球的向心加速度
C．向心力仅由太阳的引力提供
D．向心力仅由地球的引力提供
AB

火星探测项目是我国继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目。假设火星探测器在火星表面附近圆形轨道运行的周期，神舟飞船在地球表面附近的圆形轨道运行周期为，火星质量与地球质量之比为，火星半径与地球半径之比为，则与之比为
A． B． C． D．
D



(
1
)