19.3正方形课件(新版)华东师大版(34张ppt)
文档属性
| 名称 | 19.3正方形课件(新版)华东师大版(34张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-28 13:49:23 | ||
图片预览







文档简介
课件34张PPT。HS八(下)
教学课件第19章 矩形、菱形与正方形19.3 正方形学习目标1.探索并证明正方形的性质,并了解平行四边形、
矩形、菱形之间的联系和区别.(重、难点)
2.探索并证明正方形的判定.(重、难点)
3.会运用正方形的性质及判定条件进行有关的论证
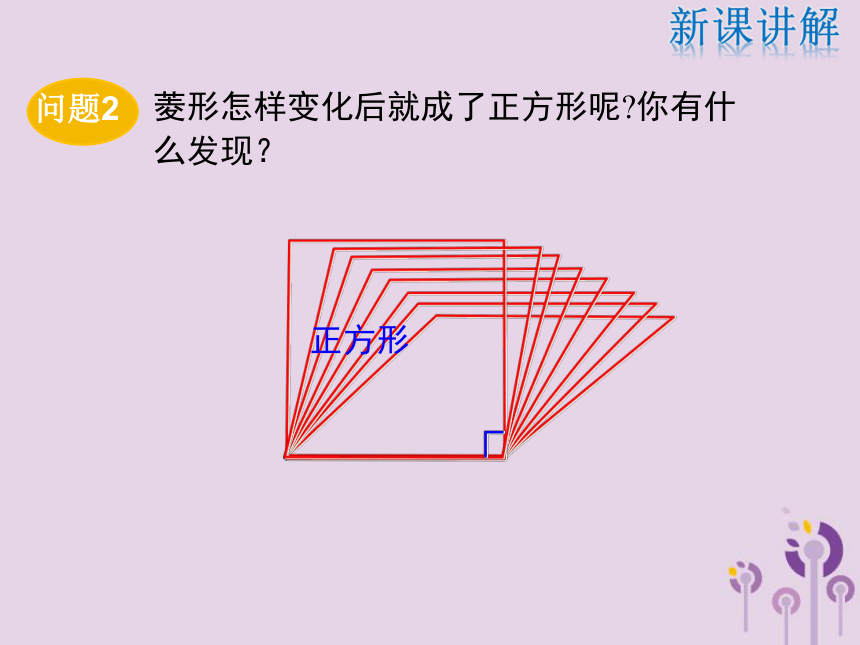
和计算 . (难点)观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.你还能举出其他的例子吗?情景引入 矩 形〃〃矩形怎样变化后就成了正方形呢?你有什么发现?正方形新课讲解正方形的性质正方形新课讲解邻边相等矩形〃〃正方形〃〃 菱 形一个角是直角正方形∟ 有一组邻边相等且有一个角是直角的平行四边形叫正方形.新课讲解★正方形的定义已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.ABCD证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形,
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
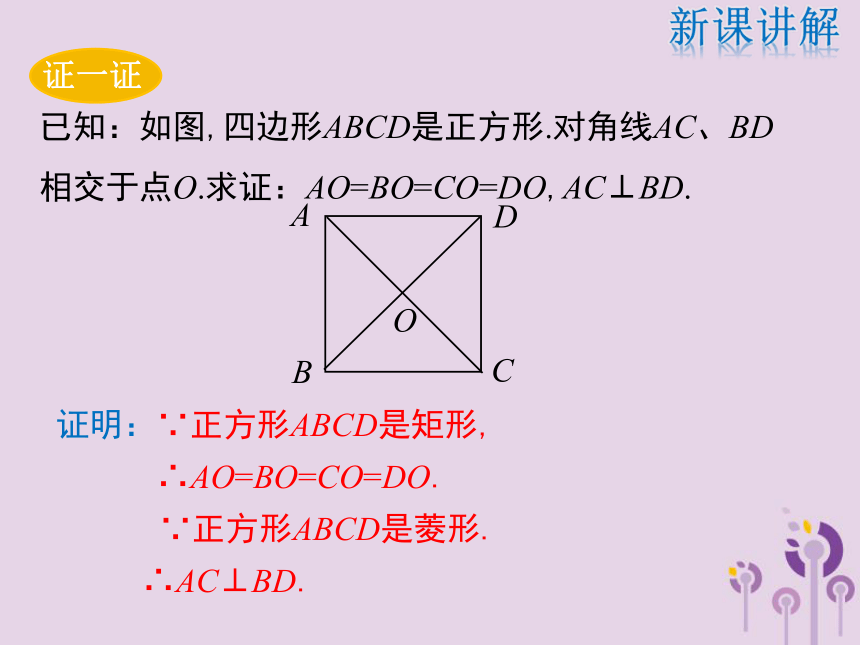
AB= BC=CD=AD.新课讲解已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.ABCDO证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.新课讲解矩形菱形正
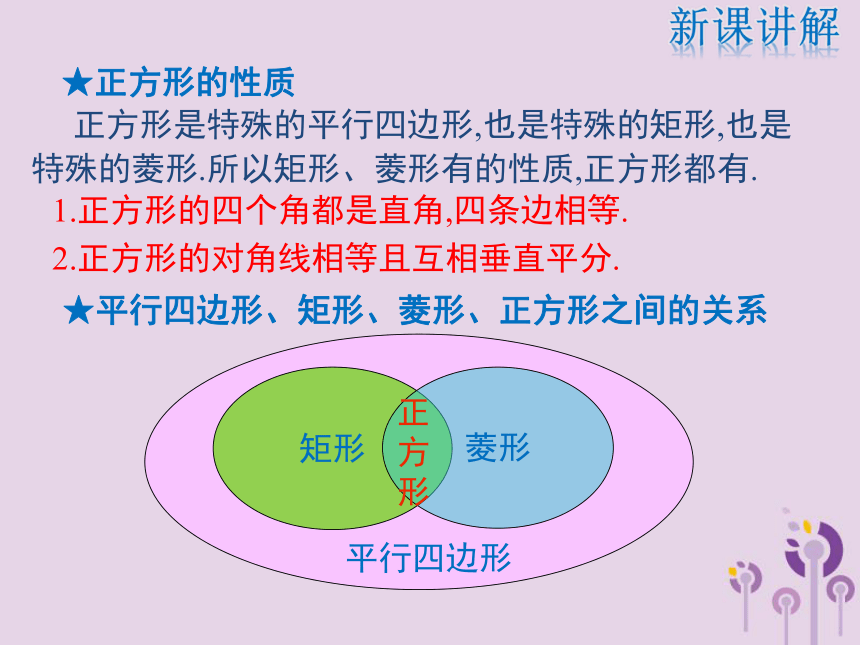
方
形平行四边形 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.1.正方形的四个角都是直角,四条边相等.
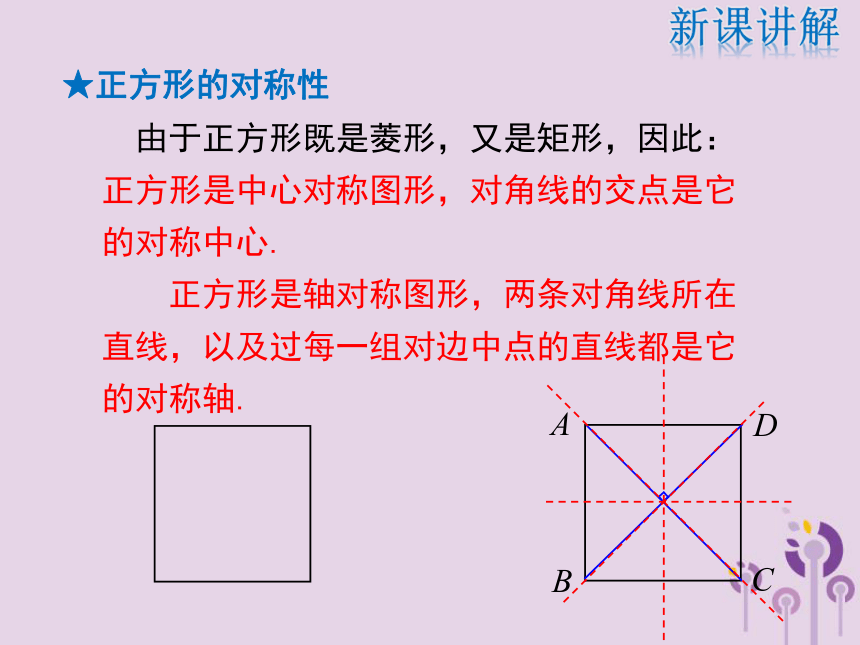
2.正方形的对角线相等且互相垂直平分.新课讲解★正方形的性质★平行四边形、矩形、菱形、正方形之间的关系 由于正方形既是菱形,又是矩形,因此:正方形是中心对称图形,对角线的交点是它的对称中心.
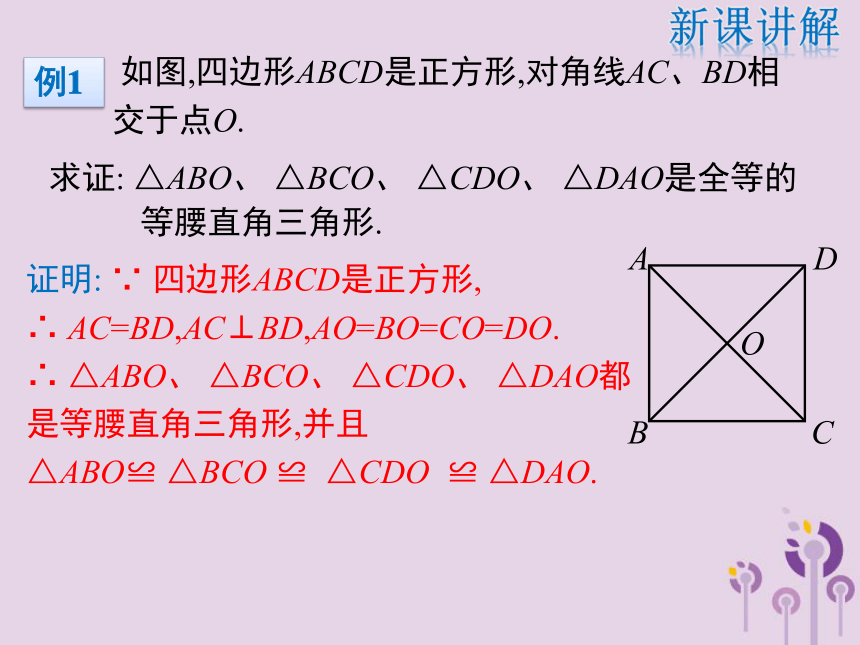
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.ABCD新课讲解★正方形的对称性 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.求证: △ABO、 △BCO、 △CDO、 △DAO是全等的
等腰直角三角形. 证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.新课讲解例1 如图,在正方形ABCD中, ΔBEC是等边三角形.
求证: ∠EAD=∠EDA=15° .证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°.
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE、△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.新课讲解例21.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等2.正方形具有而菱形不一定具有的性质( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等BD新课讲解2.如图,四边形ABCD是正方形,对角线AC与BD
相交于点O,AO=2,求正方形的周长与面积.解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,
面积为AD2=8.新课讲解 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.正方形猜想:满足怎样条件的矩形是正方形?矩形正方形一组邻边相等对角线互相垂直新课讲解正方形的判定已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO .
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴矩形ABCD是正方形.ABCDO求证:对角线互相垂直的矩形是正方形.新课讲解把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.正方形菱形猜想 :满足怎样条件的菱形是正方形?正方形一个角是直角对角线相等已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴菱形ABCD是正方形.ABCDO求证:对角线相等的菱形是正方形.新课讲解正方形判定的几条途径:正方形正方形++先判定菱形先判定矩形矩形条件(二选一)菱形条件(二选一)一个直角或一组邻边相等对角线相等或对角线垂直新课讲解★正方形的判定在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BCCABCDO新课讲解 在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?解答:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.分析:由已知可证△AEN≌△BFE≌
△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.新课讲解例3在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .新课讲解证明:∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,
∴四边形EDFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB,
∴ DE=DG.
同理得DG=DF,∴ED=DF,
∴矩形EDFC是正方形. 如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.
求证:四边形CEDF为正方形.ABCDEFG新课讲解例4 如图,正方形ABCD,动点E在AC上,AF⊥AC,
垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),
问四边形AFBE是什么特殊四边形?说明理由.(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB ,∠DAE=∠BAF ,AE=AF ,
∴△ADE≌△ABF(SAS),∴BF=DE.新课讲解例5(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE= AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴四边形AFBE为平行四边形,
∵∠FAE=90°,AF=AE,
∴平行四边形AFBE是正方形.新课讲解2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2 A1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等 A随堂即练3.在正方形ABCD中,∠ADB= ,∠DAC= , ∠BOC= .
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .45°90°22.5°第3题第4题45°随堂即练5.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA
=90°,请添加一个条件____________________,
可得出该四边形是正方形.AB=BC(答案不唯一)ABCDO6.已知四边形ABCD是平行四边形,再从①AB=BC,
②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,
选两个作为补充条件后,使得四边形ABCD是正方形,
其中错误的是_________________(只填写序号).②③(答案不唯一)随堂即练7.如图,正方形ABCD的边长为1cm,AC为对角线,
AE平分∠BAC,EF⊥AC,求BE的长.解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=( -1)cm,
∴BE=( -1)cm.随堂即练8. 如图,在正方形ABCD中,E为CD上一点,F为BC边
延长线上一点,且CE=CF. BE与DF之间有怎样的关
系?请说明理由.解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
∴∠DCF=180°-∠BCE=90°.
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.ABDCFE随堂即练延长BE交DF于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°,
∴∠CBE+∠F=90° ,
∴∠BMF=90°.
∴BE⊥DF.ABDFECM随堂即练1.四个角都是直角2.四条边都相等3.对角线相等且互相垂直平分正方形的性质性质定义有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.课堂总结5种判定方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等课堂总结★平行四边形、矩形、菱形、正方形的判定小结
教学课件第19章 矩形、菱形与正方形19.3 正方形学习目标1.探索并证明正方形的性质,并了解平行四边形、
矩形、菱形之间的联系和区别.(重、难点)
2.探索并证明正方形的判定.(重、难点)
3.会运用正方形的性质及判定条件进行有关的论证
和计算 . (难点)观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.你还能举出其他的例子吗?情景引入 矩 形〃〃矩形怎样变化后就成了正方形呢?你有什么发现?正方形新课讲解正方形的性质正方形新课讲解邻边相等矩形〃〃正方形〃〃 菱 形一个角是直角正方形∟ 有一组邻边相等且有一个角是直角的平行四边形叫正方形.新课讲解★正方形的定义已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.ABCD证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形,
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.新课讲解已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.ABCDO证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.新课讲解矩形菱形正
方
形平行四边形 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.新课讲解★正方形的性质★平行四边形、矩形、菱形、正方形之间的关系 由于正方形既是菱形,又是矩形,因此:正方形是中心对称图形,对角线的交点是它的对称中心.
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.ABCD新课讲解★正方形的对称性 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.求证: △ABO、 △BCO、 △CDO、 △DAO是全等的
等腰直角三角形. 证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.新课讲解例1 如图,在正方形ABCD中, ΔBEC是等边三角形.
求证: ∠EAD=∠EDA=15° .证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°.
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE、△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.新课讲解例21.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等2.正方形具有而菱形不一定具有的性质( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等BD新课讲解2.如图,四边形ABCD是正方形,对角线AC与BD
相交于点O,AO=2,求正方形的周长与面积.解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,
面积为AD2=8.新课讲解 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.正方形猜想:满足怎样条件的矩形是正方形?矩形正方形一组邻边相等对角线互相垂直新课讲解正方形的判定已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO .
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴矩形ABCD是正方形.ABCDO求证:对角线互相垂直的矩形是正方形.新课讲解把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.正方形菱形猜想 :满足怎样条件的菱形是正方形?正方形一个角是直角对角线相等已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴菱形ABCD是正方形.ABCDO求证:对角线相等的菱形是正方形.新课讲解正方形判定的几条途径:正方形正方形++先判定菱形先判定矩形矩形条件(二选一)菱形条件(二选一)一个直角或一组邻边相等对角线相等或对角线垂直新课讲解★正方形的判定在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BCCABCDO新课讲解 在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?解答:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.分析:由已知可证△AEN≌△BFE≌
△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.新课讲解例3在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .新课讲解证明:∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,
∴四边形EDFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB,
∴ DE=DG.
同理得DG=DF,∴ED=DF,
∴矩形EDFC是正方形. 如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.
求证:四边形CEDF为正方形.ABCDEFG新课讲解例4 如图,正方形ABCD,动点E在AC上,AF⊥AC,
垂足为A,AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),
问四边形AFBE是什么特殊四边形?说明理由.(1)证明:∵正方形ABCD,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠EAD,
在△ADE和△ABF中,
AD=AB ,∠DAE=∠BAF ,AE=AF ,
∴△ADE≌△ABF(SAS),∴BF=DE.新课讲解例5(2)解:当点E运动到AC的中点时四边形AFBE是正方形,
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE= AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEC=90°,
∴BE∥AF,
∵BE=AF,
∴四边形AFBE为平行四边形,
∵∠FAE=90°,AF=AE,
∴平行四边形AFBE是正方形.新课讲解2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2 A1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等 A随堂即练3.在正方形ABCD中,∠ADB= ,∠DAC= , ∠BOC= .
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .45°90°22.5°第3题第4题45°随堂即练5.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA
=90°,请添加一个条件____________________,
可得出该四边形是正方形.AB=BC(答案不唯一)ABCDO6.已知四边形ABCD是平行四边形,再从①AB=BC,
②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,
选两个作为补充条件后,使得四边形ABCD是正方形,
其中错误的是_________________(只填写序号).②③(答案不唯一)随堂即练7.如图,正方形ABCD的边长为1cm,AC为对角线,
AE平分∠BAC,EF⊥AC,求BE的长.解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=( -1)cm,
∴BE=( -1)cm.随堂即练8. 如图,在正方形ABCD中,E为CD上一点,F为BC边
延长线上一点,且CE=CF. BE与DF之间有怎样的关
系?请说明理由.解:BE=DF,且BE⊥DF.理由如下:
∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
∴∠DCF=180°-∠BCE=90°.
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.ABDCFE随堂即练延长BE交DF于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°,
∴∠CBE+∠F=90° ,
∴∠BMF=90°.
∴BE⊥DF.ABDFECM随堂即练1.四个角都是直角2.四条边都相等3.对角线相等且互相垂直平分正方形的性质性质定义有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.课堂总结5种判定方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等课堂总结★平行四边形、矩形、菱形、正方形的判定小结
