16.4 碰撞 24张PPT
文档属性
| 名称 | 16.4 碰撞 24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-28 12:58:06 | ||
图片预览







文档简介
第十六章 动量守恒定律
4 碰撞
碰撞的共同特点有哪些?
相互作用时间极短,速度变化很快, 相互作用力很大.
动量一定守恒!
机械能一定守恒吗?
温故而知新
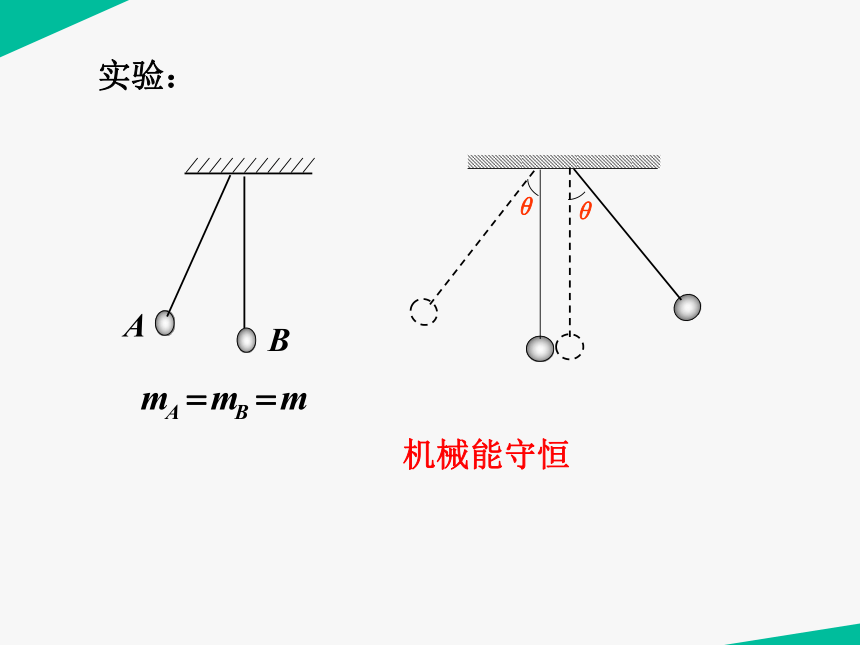
机械能守恒
实验:
A
B
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
碰撞过程中有机械能损失
理论论证
弹性碰撞:碰撞过程中机械能守恒;
非弹性碰撞:碰撞过程中机械能不守恒;
从能量变化方面分类
一、弹性碰撞和非弹性碰撞
例如:钢球、玻璃球的碰撞
动能
动能
弹性势能
例如:木球、橡皮泥球的碰撞
动能
动能
弹性势能
内能
完全非弹性碰撞:是非弹性碰撞的特例,碰后两物体粘在一起运动,机械能损失最大.
“碰撞过程”的制约
①动量制约(系统动量守恒的原则):即碰撞过程必须受到“动量守恒定律的制约”;
②动能制约:即在碰撞过程,碰撞双方的总动能不会增加;
③运动制约:即碰撞过程还将受到运动的合理性要求的制约. [碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理.]
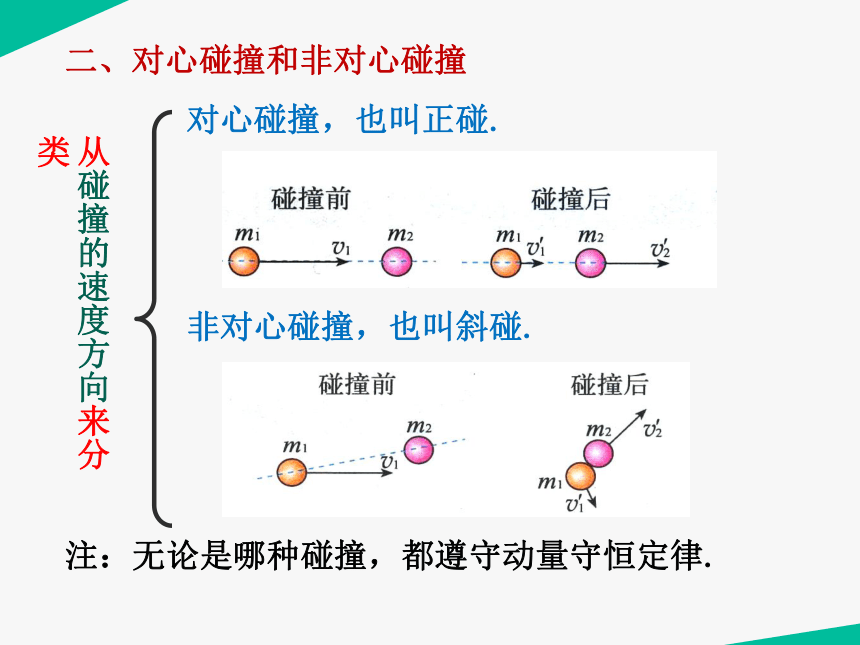
对心碰撞,也叫正碰.
非对心碰撞,也叫斜碰.
从碰撞的速度方向来分类
注:无论是哪种碰撞,都遵守动量守恒定律.
二、对心碰撞和非对心碰撞
一维弹性碰撞的分析:
若 m1 = m2,则 v1? 0,v2? = ,
(2) 若 m1 > m2, 则 v1? 0, v2? 0,
(3) 若 m1 < m2,则 v1? 0,v2? 0,
深入讨论
=
v1
>
>
<
>
(5) 若 m1 >> m2 ,则 v1? ≈ ,v2? ≈ ,
极小碰极大,大不变,小等速反弹
极大碰极小,大不变,小加倍
(4) 若 m1 << m2 ,则 v1? ≈ ,v2? ≈ ,
v1
2v1
-v1
0
例1.质量为m速度为v的A球,跟质量为3 m的静止B球发生正碰,可能是弹性碰撞,也可能非弹性碰撞,碰后B球的速度可能是以下值吗?
A. 0.6 v B. 0.4v C. 0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
所以,只有0.4v是速度可能值
例2.在光滑水平面上,动能为E0、动量的大小为P0的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰撞后球1的动能和动量的大小分别记为E1、P1,球2的动能和动量的大小分别记为E2、P2,则必有( )
A. E1C. E2>E0 D. P2>P0
ABD
例3.如图所示,一质量为m的子弹以水平速度 v0飞向小球,小球的质量为M,悬挂小球的绳长为L,子弹击中小球并留在其中,求:
(1)子弹打小球过程中所产生的热量.
(2)小球向右摆起的最大高度.
L
解:在子弹打进小球的过程中,根据动量守恒定律,有
根据能量守恒,系统减少的动能等于摩擦产生的热能
子弹和小球一起共同摆至最高点的过程,根据机械能守恒定律,有
解得摆起的最大高度
散射现象遵循动量守恒定律,是研究物质结构的重要方法,查德威克利用散射现象发现了中子.
微观粒子相互接近时并不直接接触,发生对心碰撞的概率很小,大多数粒子在碰撞后飞向四面八方,因此微观粒子的碰撞又叫散射.
三、散射—微观粒子的碰撞
碰撞的三大原则
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:若碰后两物体同向运动,则碰撞后后面物体的速度一定小于或等于前面物体的速度(否则碰撞没有结束,还要发生碰撞).
自主检测
.
1.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为6 g·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 g·m/s,则 ( )
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5
B.左方是A球,碰撞后A、B两球速度大小之比为1∶10
C.右方是A球,碰撞后A、B两球速度大小之比为2∶5
D.右方是A球,碰撞后A、B两球速度大小之比为1∶10
解析:由已知得,碰撞前A球的速度大于B球,则左方是A球.碰撞后A球的动量增量为-4 g·m/s,则B球的动量增量为4 g·m/s,所以碰后A球的动量为2 g·m/s,B球的动量为10 g·m/s,即mAvA=2 g·m/s,mBvB=10 g·m/s,且mB=2mA,vA∶vB=2∶5,所以,选项A正确.
答案:A
2.如图所示,竖直平面内的圆弧轨道下端与水平桌面相切,小滑块A和B分别静止在圆弧轨道的最高点和最低点.现将A无初速度释放,A与B碰撞后结合为一个整体,并沿水平桌面滑动.已知圆弧轨道光滑,半径R=0.2 m;A和B的质量相等;A和B整体与桌面之间的动摩擦因数μ=0.2.重力加速度g取10 m/s2.求:
(1)碰撞前瞬间A的速率v ;
(2)碰撞后瞬间A和B整体的速率v′;
(3)A和B整体在桌面上滑动的距离l.
解析:设滑块的质量为m.
(1)根据机械能守恒定律 mgR= mv2
得碰撞前瞬间A的速率v=2 m/s.
(2)根据动量守恒定律 mv=2mv′
得碰撞后瞬间A和B整体的速率 v′= v=1 m/s.
(3)根据动能定理
×2mv′2=μ·2mgl
得A和B整体沿水平桌面滑动的距离 l=0.25 m.
答案:(1)2 m/s (2)1 m/s (3)0.25 m
基本知识点
弹性碰撞→动量、机械能守恒
非弹性碰撞→动量守恒、机械能有损失
完全非弹性碰撞→动量守恒、机械能损失最大
基本思想方法
猜想
推论
小结
对心碰撞(正碰)→碰撞前后速度沿球心连线
非对心碰撞(斜碰)→碰撞前后速度不共线
验证
4 碰撞
碰撞的共同特点有哪些?
相互作用时间极短,速度变化很快, 相互作用力很大.
动量一定守恒!
机械能一定守恒吗?
温故而知新
机械能守恒
实验:
A
B
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
碰撞过程中有机械能损失
理论论证
弹性碰撞:碰撞过程中机械能守恒;
非弹性碰撞:碰撞过程中机械能不守恒;
从能量变化方面分类
一、弹性碰撞和非弹性碰撞
例如:钢球、玻璃球的碰撞
动能
动能
弹性势能
例如:木球、橡皮泥球的碰撞
动能
动能
弹性势能
内能
完全非弹性碰撞:是非弹性碰撞的特例,碰后两物体粘在一起运动,机械能损失最大.
“碰撞过程”的制约
①动量制约(系统动量守恒的原则):即碰撞过程必须受到“动量守恒定律的制约”;
②动能制约:即在碰撞过程,碰撞双方的总动能不会增加;
③运动制约:即碰撞过程还将受到运动的合理性要求的制约. [碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理.]
对心碰撞,也叫正碰.
非对心碰撞,也叫斜碰.
从碰撞的速度方向来分类
注:无论是哪种碰撞,都遵守动量守恒定律.
二、对心碰撞和非对心碰撞
一维弹性碰撞的分析:
若 m1 = m2,则 v1? 0,v2? = ,
(2) 若 m1 > m2, 则 v1? 0, v2? 0,
(3) 若 m1 < m2,则 v1? 0,v2? 0,
深入讨论
=
v1
>
>
<
>
(5) 若 m1 >> m2 ,则 v1? ≈ ,v2? ≈ ,
极小碰极大,大不变,小等速反弹
极大碰极小,大不变,小加倍
(4) 若 m1 << m2 ,则 v1? ≈ ,v2? ≈ ,
v1
2v1
-v1
0
例1.质量为m速度为v的A球,跟质量为3 m的静止B球发生正碰,可能是弹性碰撞,也可能非弹性碰撞,碰后B球的速度可能是以下值吗?
A. 0.6 v B. 0.4v C. 0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
所以,只有0.4v是速度可能值
例2.在光滑水平面上,动能为E0、动量的大小为P0的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰撞后球1的动能和动量的大小分别记为E1、P1,球2的动能和动量的大小分别记为E2、P2,则必有( )
A. E1
ABD
例3.如图所示,一质量为m的子弹以水平速度 v0飞向小球,小球的质量为M,悬挂小球的绳长为L,子弹击中小球并留在其中,求:
(1)子弹打小球过程中所产生的热量.
(2)小球向右摆起的最大高度.
L
解:在子弹打进小球的过程中,根据动量守恒定律,有
根据能量守恒,系统减少的动能等于摩擦产生的热能
子弹和小球一起共同摆至最高点的过程,根据机械能守恒定律,有
解得摆起的最大高度
散射现象遵循动量守恒定律,是研究物质结构的重要方法,查德威克利用散射现象发现了中子.
微观粒子相互接近时并不直接接触,发生对心碰撞的概率很小,大多数粒子在碰撞后飞向四面八方,因此微观粒子的碰撞又叫散射.
三、散射—微观粒子的碰撞
碰撞的三大原则
1.系统动量守恒原则:碰撞前后系统的总动量守恒.
2.动能不增加原则:碰撞后系统的总动能小于或等于碰撞前系统的总动能,即系统的总动能不增加.
3.物理情景可行性原则:若碰后两物体同向运动,则碰撞后后面物体的速度一定小于或等于前面物体的速度(否则碰撞没有结束,还要发生碰撞).
自主检测
.
1.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为6 g·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 g·m/s,则 ( )
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5
B.左方是A球,碰撞后A、B两球速度大小之比为1∶10
C.右方是A球,碰撞后A、B两球速度大小之比为2∶5
D.右方是A球,碰撞后A、B两球速度大小之比为1∶10
解析:由已知得,碰撞前A球的速度大于B球,则左方是A球.碰撞后A球的动量增量为-4 g·m/s,则B球的动量增量为4 g·m/s,所以碰后A球的动量为2 g·m/s,B球的动量为10 g·m/s,即mAvA=2 g·m/s,mBvB=10 g·m/s,且mB=2mA,vA∶vB=2∶5,所以,选项A正确.
答案:A
2.如图所示,竖直平面内的圆弧轨道下端与水平桌面相切,小滑块A和B分别静止在圆弧轨道的最高点和最低点.现将A无初速度释放,A与B碰撞后结合为一个整体,并沿水平桌面滑动.已知圆弧轨道光滑,半径R=0.2 m;A和B的质量相等;A和B整体与桌面之间的动摩擦因数μ=0.2.重力加速度g取10 m/s2.求:
(1)碰撞前瞬间A的速率v ;
(2)碰撞后瞬间A和B整体的速率v′;
(3)A和B整体在桌面上滑动的距离l.
解析:设滑块的质量为m.
(1)根据机械能守恒定律 mgR= mv2
得碰撞前瞬间A的速率v=2 m/s.
(2)根据动量守恒定律 mv=2mv′
得碰撞后瞬间A和B整体的速率 v′= v=1 m/s.
(3)根据动能定理
×2mv′2=μ·2mgl
得A和B整体沿水平桌面滑动的距离 l=0.25 m.
答案:(1)2 m/s (2)1 m/s (3)0.25 m
基本知识点
弹性碰撞→动量、机械能守恒
非弹性碰撞→动量守恒、机械能有损失
完全非弹性碰撞→动量守恒、机械能损失最大
基本思想方法
猜想
推论
小结
对心碰撞(正碰)→碰撞前后速度沿球心连线
非对心碰撞(斜碰)→碰撞前后速度不共线
验证
