人教版八年级下册 17.1 第1课时 勾股定理 (共25张PPT)
文档属性
| 名称 | 人教版八年级下册 17.1 第1课时 勾股定理 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-28 14:39:57 | ||
图片预览





文档简介
课件25张PPT。勾股定理人教版八年级数学(下)第十七章第一节这是2002年国际数学家大会会徽的图案.勾股定理人教版八年级数学(下)第十七章1、培养正确的观察事物分析事物能力,理解并掌握勾股定理及其证明. 2、在学生经历“观察—猜想—归纳—验证”勾股定理的过程中,发展合情推理能力,体会数形结合和从特殊到一般的思想. 3、通过对勾股定理历史的了解,感受数学文化,激发学习兴趣;在探究活动中,培养学生的合作交流意识和探索精神. 重点:探索和证明勾股定理。难点:勾股定理的推导及应用学习目标:看一看 相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?(要有一双慧眼哦)思考:
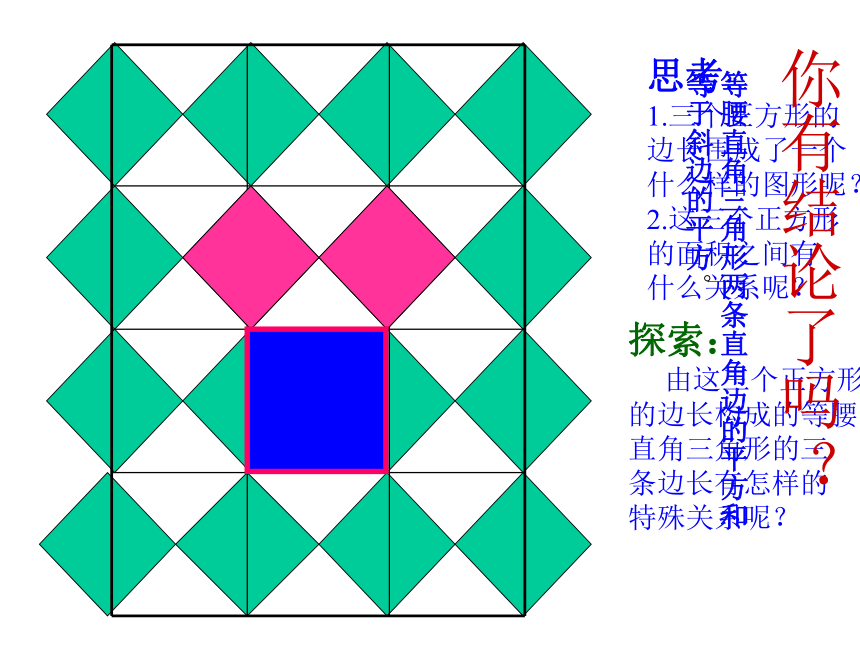
1.三个正方形的
边长围成了一个
什么样的图形呢?
2.这三个正方形
的面积之间有
什么关系呢?探索:
由这三个正方形
的边长构成的等腰
直角三角形的三
条边长有怎样的
特殊关系呢?你有结论了吗?等腰直角三角形两条直角边的平方和
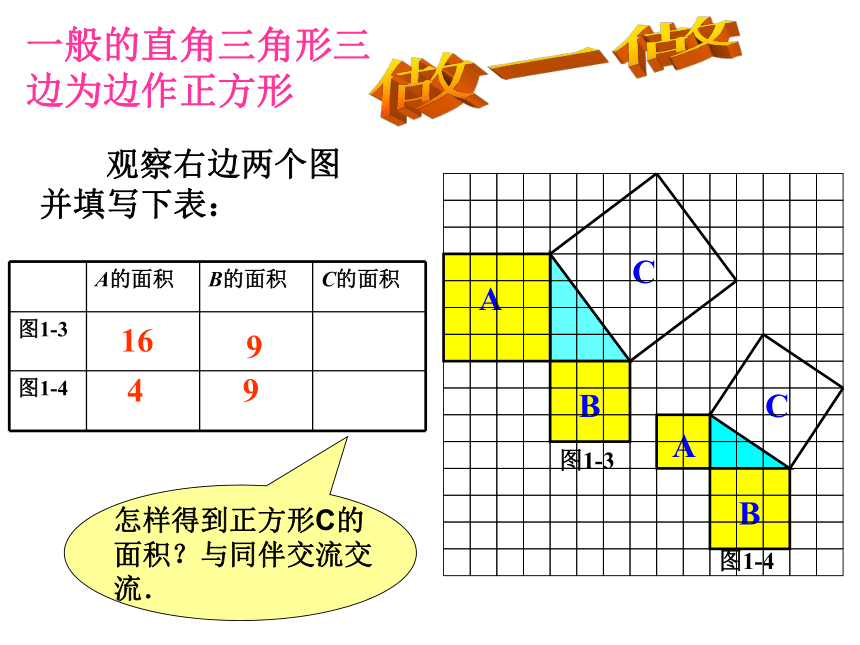
等于斜边的平方。 观察右边两个图并填写下表:16949 怎样得到正方形C的面积?与同伴交流交流.做一做一般的直角三角形三边为边作正方形
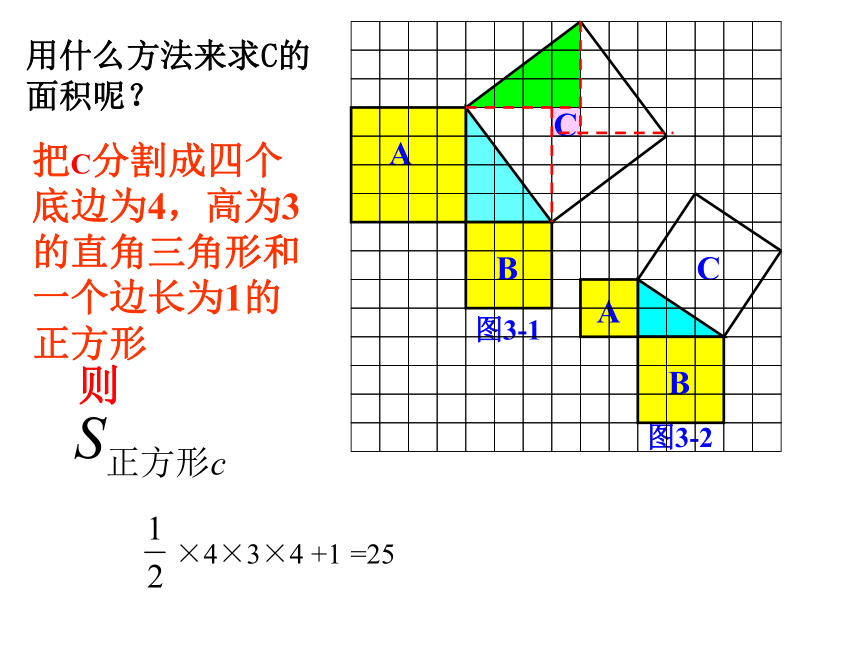
把C分割成四个底边为4,高为3的直角三角形和一个边长为1的正方形 ×4×3×4 +1则=25用什么方法来求C的面积呢?把C“补”成边长为7的正方形面积减去4个三角形的面积思考:图3-2中C的面积是多少呢呢?
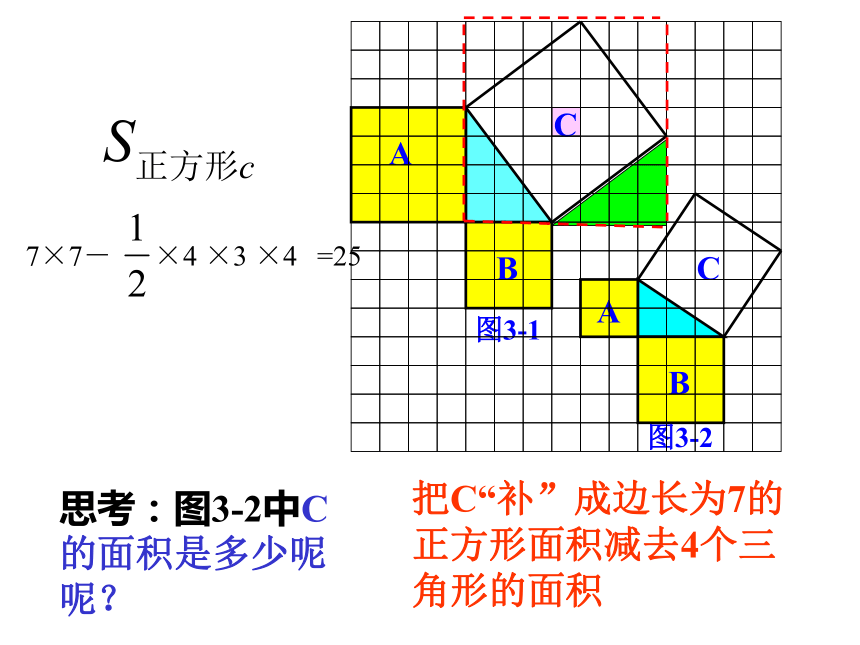
7×7-×4 ×3 ×4=25 根据前面的探究,填写下表:1694 9做一做1325 三个正方形A, B,C面积之间有什么关系?acbS A +S B =S C 通过上述讨论,你有什么发现?猜想:如果A的边长是a,B的边长是b,C的边长是c,那么两直角边a、b与斜边c 之间是什么样的关系呢?a2+b2=c2┏acb 如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。 命题1:赵爽弦图证法: 我国汉代的数学家赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形。赵爽弦图
(动动你的小手)赵爽弦图的证法∴ c2 =a2+ b2S大正方形=S小正方形+4S直角三角形
C2=(b-a)2+4× C2=a2-2ab+b2+2abb-aababcabcc2b2a2=+拼图法证明:定理:经过证明被确认为正确的命题叫做定理。如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2ABCb ac勾股定理:如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2 。 “赵爽弦图”通过对图形的切割、拼接、巧妙地用面积关系证明了勾股定理,它表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,这个图案被选为2002年在北京召开的国际数学大会的会徽。1.求下列图中未知的正方形的面积.①81144②③做一做做一做: P62540026xP的面积 =______________X=____________225BACAB=__________AC=__________BC=__________251520比一比看看谁算得快!2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C342、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )A.50米 B.120米 C.100米 D.130米130120?A如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?议一议:9m24m 小结
1.我们本节课学习了什么知识?
2.谈一谈你学完本节课的感受。
作业
教材第24页练习第1、2题
谢谢!再见!
1.三个正方形的
边长围成了一个
什么样的图形呢?
2.这三个正方形
的面积之间有
什么关系呢?探索:
由这三个正方形
的边长构成的等腰
直角三角形的三
条边长有怎样的
特殊关系呢?你有结论了吗?等腰直角三角形两条直角边的平方和
等于斜边的平方。 观察右边两个图并填写下表:16949 怎样得到正方形C的面积?与同伴交流交流.做一做一般的直角三角形三边为边作正方形
把C分割成四个底边为4,高为3的直角三角形和一个边长为1的正方形 ×4×3×4 +1则=25用什么方法来求C的面积呢?把C“补”成边长为7的正方形面积减去4个三角形的面积思考:图3-2中C的面积是多少呢呢?
7×7-×4 ×3 ×4=25 根据前面的探究,填写下表:1694 9做一做1325 三个正方形A, B,C面积之间有什么关系?acbS A +S B =S C 通过上述讨论,你有什么发现?猜想:如果A的边长是a,B的边长是b,C的边长是c,那么两直角边a、b与斜边c 之间是什么样的关系呢?a2+b2=c2┏acb 如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。 命题1:赵爽弦图证法: 我国汉代的数学家赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形。赵爽弦图
(动动你的小手)赵爽弦图的证法∴ c2 =a2+ b2S大正方形=S小正方形+4S直角三角形
C2=(b-a)2+4× C2=a2-2ab+b2+2abb-aababcabcc2b2a2=+拼图法证明:定理:经过证明被确认为正确的命题叫做定理。如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2ABCb ac勾股定理:如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2 。 “赵爽弦图”通过对图形的切割、拼接、巧妙地用面积关系证明了勾股定理,它表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,这个图案被选为2002年在北京召开的国际数学大会的会徽。1.求下列图中未知的正方形的面积.①81144②③做一做做一做: P62540026xP的面积 =______________X=____________225BACAB=__________AC=__________BC=__________251520比一比看看谁算得快!2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C342、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )A.50米 B.120米 C.100米 D.130米130120?A如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?议一议:9m24m 小结
1.我们本节课学习了什么知识?
2.谈一谈你学完本节课的感受。
作业
教材第24页练习第1、2题
谢谢!再见!
