北师大版数学七年级下册 2.3 平行线的性质 (共24张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 2.3 平行线的性质 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-28 15:18:10 | ||
图片预览



文档简介
北师大版七年级数学下册
两直线平行的条件
同位角相等
内错角相等
同旁内角互补
平行条件
复习引入:
问题1:如图,
(1)∵ ∠1____∠2 (已知)
∴ a ∥ b (同位角相等,两直线平行 )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b (? )
(3)∵ ∠2+∠4=____(已知),
∴ a ∥ b ???
=
=
内错角相等,两直线平行
180°
(同旁内角互补,两直线平行)
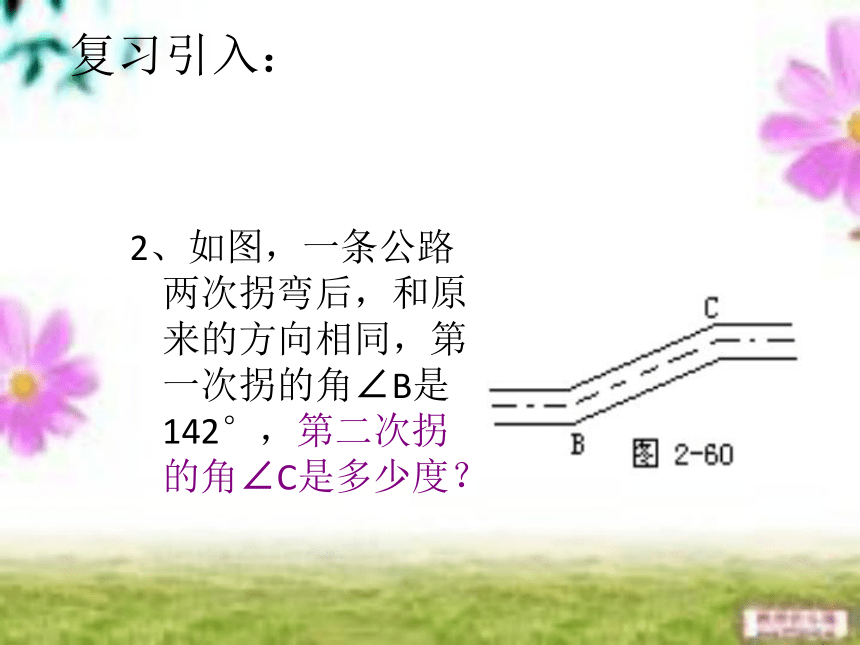
复习引入:
2、如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
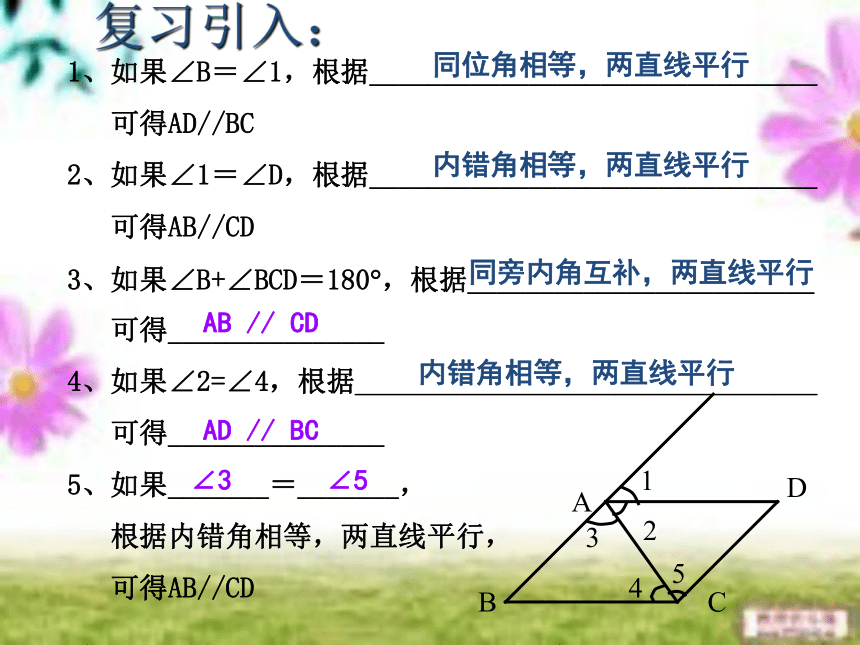
1、如果∠B=∠1,根据_______________________________
可得AD//BC
2、如果∠1=∠D,根据_______________________________
可得AB//CD
3、如果∠B+∠BCD=180?,根据________________________
可得_______________
4、如果∠2=∠4,根据________________________________
可得_______________
5、如果_______=_______,
根据内错角相等,两直线平行,
可得AB//CD
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
AB // CD
内错角相等,两直线平行
AD // BC
∠5
∠3
复习引入:
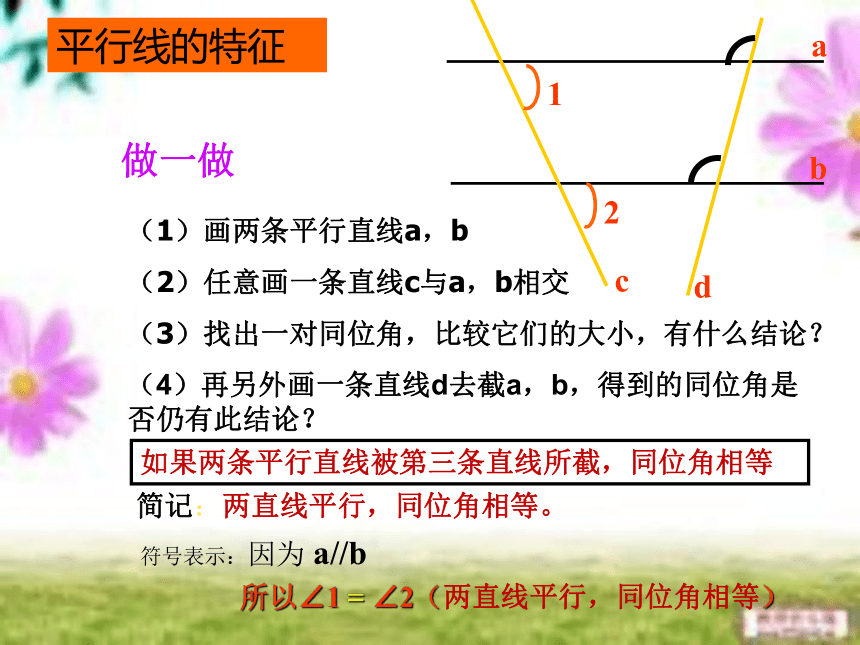
做一做
(1)画两条平行直线a,b
(2)任意画一条直线c与a,b相交
(3)找出一对同位角,比较它们的大小,有什么结论?
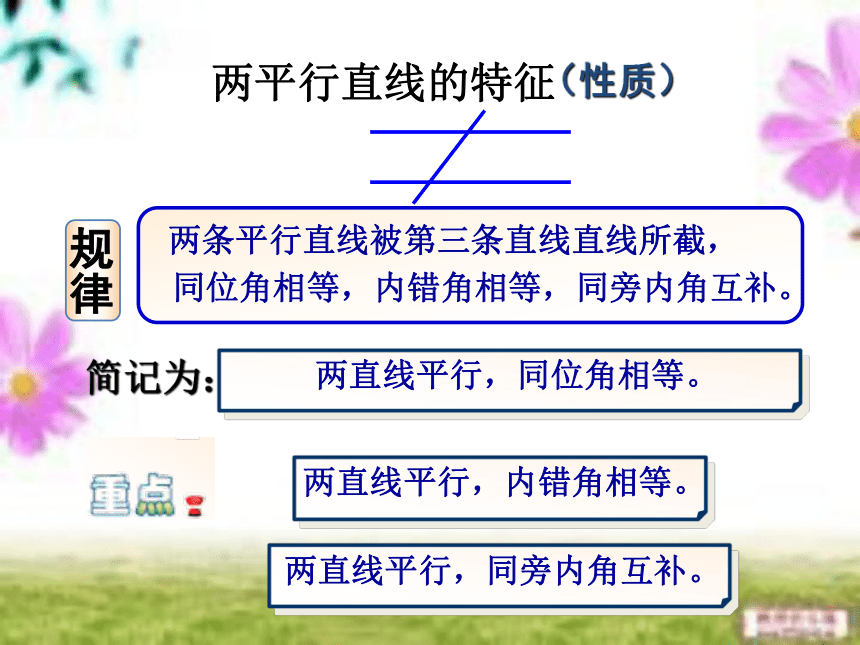
简记:两直线平行,同位角相等。
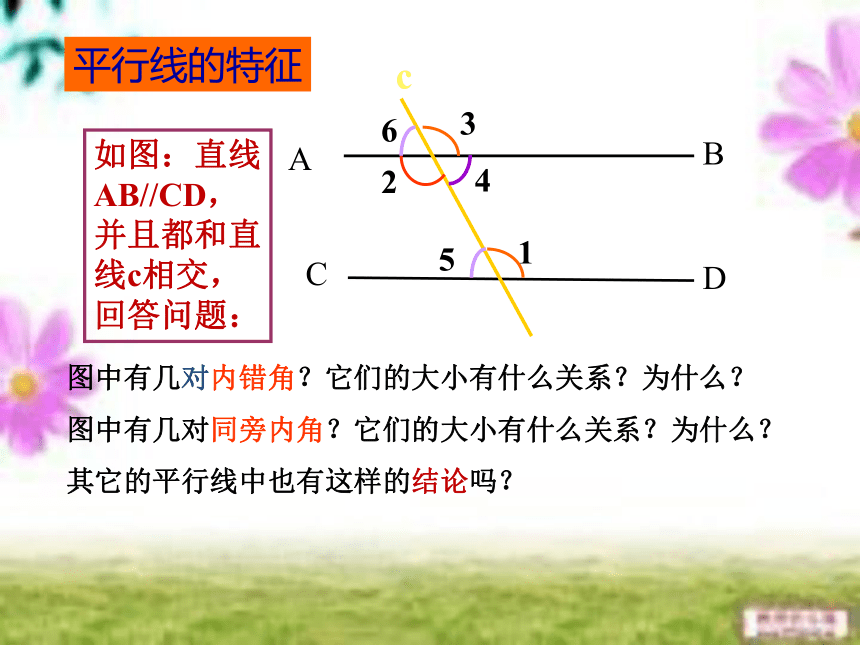
平行线的特征
a
b
c
(4)再另外画一条直线d去截a,b,得到的同位角是否仍有此结论?
d
如果两条平行直线被第三条直线所截,同位角相等
符号表示:因为 a//b
所以∠1 = ∠2(两直线平行,同位角相等)
平行线的特征
c
图中有几对内错角?它们的大小有什么关系?为什么?
图中有几对同旁内角?它们的大小有什么关系?为什么?
其它的平行线中也有这样的结论吗?
如图:直线AB//CD,并且都和直线c相交,回答问题:
简记为:
两平行直线的特征
(性质)
同位角相等,内错角相等,同旁内角互补。
两类定理的比较
两条平行直线被第三条直线直线所截,
互换。
2、使用判定定理时是
已知 ,说明 ;
角的相等或互补
两直线平行
使用性质定理时是
已知 ,说明 。
两直线平行
角的相等或互补
同位角相等 两直线平行
两直线平行 同位角相等
内错角相等 两直线平行
两直线平行 内错角相等
同旁内角互补 两直线平行
两直线平行 同旁内角互补
判定定理(平行条件) 性质定理(平行特征)
条件 结论 条件 结论
两直线平行
同位角相等
内错角相等
同旁内角互补
平行特征
平行条件
如图:一束平行光线AB和DE射向一个水平镜面后 被反射,
(1 )∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE ∴∠1=∠3。
相等:∠1=∠3;
你知道理由吗?
两直线平行
同位角相等
(2 )反射光线BC与EF也平行吗?
∵ ∠2=∠4 ∴ BC∥EF 。
平行:
又 ∠1=∠2 ,∠3=∠4
∴ ∠2=∠4。
此时∠1=∠2 , ∠3=∠4 。
∠2 =∠4 。
你知道理由吗?
同位角相等
两直线平行
∠1=∠2 ∠3=∠4
1、如图所示,AB∥CD,AC∥BD。
分别找出与∠1相等或互补的角。
如图,与∠1相等的角有:
∠3, ∠5, ∠7, ∠9,
∠11, ∠13, ∠15;
与∠1互补的角有:
∠2, ∠4, ∠6, ∠8,
∠10, ∠12, ∠14, ∠16 ;
解:
A
B
C
D
115°
110°
如图,是举世闻名的三星堆考古中发掘出的
一个梯形残缺玉片,工作人员从玉片上已经量得A=115°,∠D=100°。已知梯形的两底AD//BC,
请你求出另外两个角的度数。
解:
∵ AD//BC(已知)
∴?A+ ? B =180°
(两直线平行,同旁内角互补)
∴?B =180°- ?A
=180°- 115°
=65 °
同理:?C =180°- ?D =180°- 110° =70 °
1、如果AD//BC,根据__________________________
可得∠B=∠1
2、如果AB//CD,根据___________________________
可得∠D=∠1
3、如果AD//BC,根据___________________________
可得∠C+_______=180?
1
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
∠D
4.如图a∥b,c ∥d,
∠1=60°,
那么 ①∠2=____
②∠3=____
③ ∠4=____
④ ∠5=____
120°
60°
60°
60°
a
2
b
60°
d
1
5
3
4
c
例1:如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。
1
解:
∵ AG//CF(已知)
∴ ∠A=∠1
(两直线平行,同位角相等)
又∵AB//CD(已知)
∴ ∠1=∠C
(两直线平行,同位角相等)
∴ ∠A=∠C
(等量代换)
∵ ∠A=40?
∴ ∠C=40?
例2 如图所示 ∠1 =∠2
求证 : ∠3 =∠4
证明:∵ ∠1 =∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行,内错角相等)
1、如图、已知? 1=60°、?2=60°
?3=78°、求?4.
解: ∵?1=60°、?2=60°
∴ ?3+ ?4=180°(两直线平行,同旁内角互补)
∴ ?4=180°-60°=120°
∴AB//CD(内错角相等,两直线平行)
练一练:
练一练:
2、如图,⑴如果AB//PC,∠P=35°,那么∠PAB=_____;
145°
58°
3
180°
⑵如果AD//BC,∠2=18°,
∠5=40°,那么ABC=_____;
⑶如果AP//BD,那么∠P=∠___;
⑷如果AB//CD,那么∠ABC+ ∠C =____.
议一议 :
如图,直线AB//CD,E在AB与CD之间,
且∠B=61°,∠D=34°.
求∠BED的度数.
1
2
第一个算出地球周长的人
2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的爱拉斯托塞。 爱拉斯托塞博学多才。
细心的爱拉斯托塞发现:离亚历山大城A约800公里的塞尼城S,夏日正午的阳光可以一直照到井底,也就是说,在那一时刻,太阳正好悬挂在塞尼城的正上方E,阳光能够只指地心O.而在此时他所在的亚历山大城阳光却不能直接射到水井的底部.爱拉斯托塞在地上竖起一根小
木棍AC,测量天顶方向AB与太阳方向AD之间的夹角∠1,发现这个夹角等于360°的1/50 .
E
D
B
1
S
A
O
2
C
E
D
B
1
S
A
O
2
C
由于太阳离地球非常遥远,把射到地球上的阳光看作是彼此平行的,
即AD ∥SE,所以∠1= ∠2.
两直线平行,同位角相等。
那么∠2的度数也等于360°的1/50 ,所以,亚历山大城到塞尼城的距离弧AS也等于整个地球周长的1/50 .而亚历山大城到塞尼城的距离约为800公里,800×50=40000公里,这是一个相当精确的结果.
两直线平行
同位角相等
内错角相等
同旁内角互补
平行特征
平行条件
这里的关键之一是要搞清“已知”了什么,得到
的是什么样的“结论”.这样才能确保正确的应用,
不发生错误.
两直线平行的条件
同位角相等
内错角相等
同旁内角互补
平行条件
复习引入:
问题1:如图,
(1)∵ ∠1____∠2 (已知)
∴ a ∥ b (同位角相等,两直线平行 )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b (? )
(3)∵ ∠2+∠4=____(已知),
∴ a ∥ b ???
=
=
内错角相等,两直线平行
180°
(同旁内角互补,两直线平行)
复习引入:
2、如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
1、如果∠B=∠1,根据_______________________________
可得AD//BC
2、如果∠1=∠D,根据_______________________________
可得AB//CD
3、如果∠B+∠BCD=180?,根据________________________
可得_______________
4、如果∠2=∠4,根据________________________________
可得_______________
5、如果_______=_______,
根据内错角相等,两直线平行,
可得AB//CD
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
AB // CD
内错角相等,两直线平行
AD // BC
∠5
∠3
复习引入:
做一做
(1)画两条平行直线a,b
(2)任意画一条直线c与a,b相交
(3)找出一对同位角,比较它们的大小,有什么结论?
简记:两直线平行,同位角相等。
平行线的特征
a
b
c
(4)再另外画一条直线d去截a,b,得到的同位角是否仍有此结论?
d
如果两条平行直线被第三条直线所截,同位角相等
符号表示:因为 a//b
所以∠1 = ∠2(两直线平行,同位角相等)
平行线的特征
c
图中有几对内错角?它们的大小有什么关系?为什么?
图中有几对同旁内角?它们的大小有什么关系?为什么?
其它的平行线中也有这样的结论吗?
如图:直线AB//CD,并且都和直线c相交,回答问题:
简记为:
两平行直线的特征
(性质)
同位角相等,内错角相等,同旁内角互补。
两类定理的比较
两条平行直线被第三条直线直线所截,
互换。
2、使用判定定理时是
已知 ,说明 ;
角的相等或互补
两直线平行
使用性质定理时是
已知 ,说明 。
两直线平行
角的相等或互补
同位角相等 两直线平行
两直线平行 同位角相等
内错角相等 两直线平行
两直线平行 内错角相等
同旁内角互补 两直线平行
两直线平行 同旁内角互补
判定定理(平行条件) 性质定理(平行特征)
条件 结论 条件 结论
两直线平行
同位角相等
内错角相等
同旁内角互补
平行特征
平行条件
如图:一束平行光线AB和DE射向一个水平镜面后 被反射,
(1 )∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE ∴∠1=∠3。
相等:∠1=∠3;
你知道理由吗?
两直线平行
同位角相等
(2 )反射光线BC与EF也平行吗?
∵ ∠2=∠4 ∴ BC∥EF 。
平行:
又 ∠1=∠2 ,∠3=∠4
∴ ∠2=∠4。
此时∠1=∠2 , ∠3=∠4 。
∠2 =∠4 。
你知道理由吗?
同位角相等
两直线平行
∠1=∠2 ∠3=∠4
1、如图所示,AB∥CD,AC∥BD。
分别找出与∠1相等或互补的角。
如图,与∠1相等的角有:
∠3, ∠5, ∠7, ∠9,
∠11, ∠13, ∠15;
与∠1互补的角有:
∠2, ∠4, ∠6, ∠8,
∠10, ∠12, ∠14, ∠16 ;
解:
A
B
C
D
115°
110°
如图,是举世闻名的三星堆考古中发掘出的
一个梯形残缺玉片,工作人员从玉片上已经量得A=115°,∠D=100°。已知梯形的两底AD//BC,
请你求出另外两个角的度数。
解:
∵ AD//BC(已知)
∴?A+ ? B =180°
(两直线平行,同旁内角互补)
∴?B =180°- ?A
=180°- 115°
=65 °
同理:?C =180°- ?D =180°- 110° =70 °
1、如果AD//BC,根据__________________________
可得∠B=∠1
2、如果AB//CD,根据___________________________
可得∠D=∠1
3、如果AD//BC,根据___________________________
可得∠C+_______=180?
1
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
∠D
4.如图a∥b,c ∥d,
∠1=60°,
那么 ①∠2=____
②∠3=____
③ ∠4=____
④ ∠5=____
120°
60°
60°
60°
a
2
b
60°
d
1
5
3
4
c
例1:如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。
1
解:
∵ AG//CF(已知)
∴ ∠A=∠1
(两直线平行,同位角相等)
又∵AB//CD(已知)
∴ ∠1=∠C
(两直线平行,同位角相等)
∴ ∠A=∠C
(等量代换)
∵ ∠A=40?
∴ ∠C=40?
例2 如图所示 ∠1 =∠2
求证 : ∠3 =∠4
证明:∵ ∠1 =∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行,内错角相等)
1、如图、已知? 1=60°、?2=60°
?3=78°、求?4.
解: ∵?1=60°、?2=60°
∴ ?3+ ?4=180°(两直线平行,同旁内角互补)
∴ ?4=180°-60°=120°
∴AB//CD(内错角相等,两直线平行)
练一练:
练一练:
2、如图,⑴如果AB//PC,∠P=35°,那么∠PAB=_____;
145°
58°
3
180°
⑵如果AD//BC,∠2=18°,
∠5=40°,那么ABC=_____;
⑶如果AP//BD,那么∠P=∠___;
⑷如果AB//CD,那么∠ABC+ ∠C =____.
议一议 :
如图,直线AB//CD,E在AB与CD之间,
且∠B=61°,∠D=34°.
求∠BED的度数.
1
2
第一个算出地球周长的人
2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的爱拉斯托塞。 爱拉斯托塞博学多才。
细心的爱拉斯托塞发现:离亚历山大城A约800公里的塞尼城S,夏日正午的阳光可以一直照到井底,也就是说,在那一时刻,太阳正好悬挂在塞尼城的正上方E,阳光能够只指地心O.而在此时他所在的亚历山大城阳光却不能直接射到水井的底部.爱拉斯托塞在地上竖起一根小
木棍AC,测量天顶方向AB与太阳方向AD之间的夹角∠1,发现这个夹角等于360°的1/50 .
E
D
B
1
S
A
O
2
C
E
D
B
1
S
A
O
2
C
由于太阳离地球非常遥远,把射到地球上的阳光看作是彼此平行的,
即AD ∥SE,所以∠1= ∠2.
两直线平行,同位角相等。
那么∠2的度数也等于360°的1/50 ,所以,亚历山大城到塞尼城的距离弧AS也等于整个地球周长的1/50 .而亚历山大城到塞尼城的距离约为800公里,800×50=40000公里,这是一个相当精确的结果.
两直线平行
同位角相等
内错角相等
同旁内角互补
平行特征
平行条件
这里的关键之一是要搞清“已知”了什么,得到
的是什么样的“结论”.这样才能确保正确的应用,
不发生错误.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
