2018-2019年人教版八下数学第20章 数据的分析单元测试卷(解析版)
文档属性
| 名称 | 2018-2019年人教版八下数学第20章 数据的分析单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-28 00:00:00 | ||
图片预览




文档简介
2019年人教版八下数学《第20章 数据的分析》单元测试卷
一.选择题(共10小题)
1.已知5个数a1、a2、a3、a4、a5的平均数是a,则数据a1+1,a2+2,a3+3,a4+4,a5+5的平均数为( )
A.a B.a+3 C. a D.a+15
2.一组数据x1,x2,x3,x4,x5的平均数是x,另一组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是( )
A.x B.2x C.2x+5 D.10x+25
3.某中学初三(1)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男、女生的人数之比为( )
A.1:2 B.2:1 C.3:2 D.2:3
4.某居民区的月底统计用电情况如下,其中3户用电45度,5户用电50度,6户用电42度,则平均用电( )度.
A.41 B.42 C.45.5 D.46
5.本市5月份某一周每天的最高气温统计如下表:
温度/℃ 22 24 26 29
天数 2 1 3 1
则这组数据的中位数和平均数分别是( )
A.24,25 B.25,26 C.26,24 D.26,25
6.已知一组数据6,8,10,x的中位数与平均数相等,这样的x有( )
A.1个 B.2个
C.3个 D.4个以上(含4个)
7.在一组数据3,4,4,6,8中,下列说法错误的是( )
A.它的众数是4 B.它的平均数是5
C.它的中位数是5 D.它的众数等于中位数
8.抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
A.20,20 B.30,20 C.30,30 D.20,30
9.为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表,关于这10户家庭的月用电量说法正确的是( )
月用电量(度) 25 30 40 50 60
户数 1 2 4 2 1
A.极差是3 B.众数是4
C.中位数40 D.平均数是20.5
10.一次数学测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85,98.关于这组数据说法错误的是( )
A.极差是20 B.中位数是91 C.众数是98 D.平均数是91
二.填空题(共5小题)
11.小明等五名同学四月份参加某次数学测验的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为 .
12.在学校的卫生检查中,规定各班的教室卫生成绩占30%,环境卫生成绩占40%,个人卫生成绩占30%.八年级一班这三项成绩分别为85分,90分和95分,求该班卫生检查的总成绩 .
13.某同学在使用计算器求20个数的时候,将88误输入为8,那么由此求出的平均数与实际平均数的差为 .
14.一组数据:25,29,20,x,14,它的中位数是24,则这组数据的平均数为 .
15.某学习小组,对我市居民家庭年收入进行调查,并将数据绘制成图,家庭年收入的众数为 元;这些家庭年收入的平均数为 元.
三.解答题(共5小题)
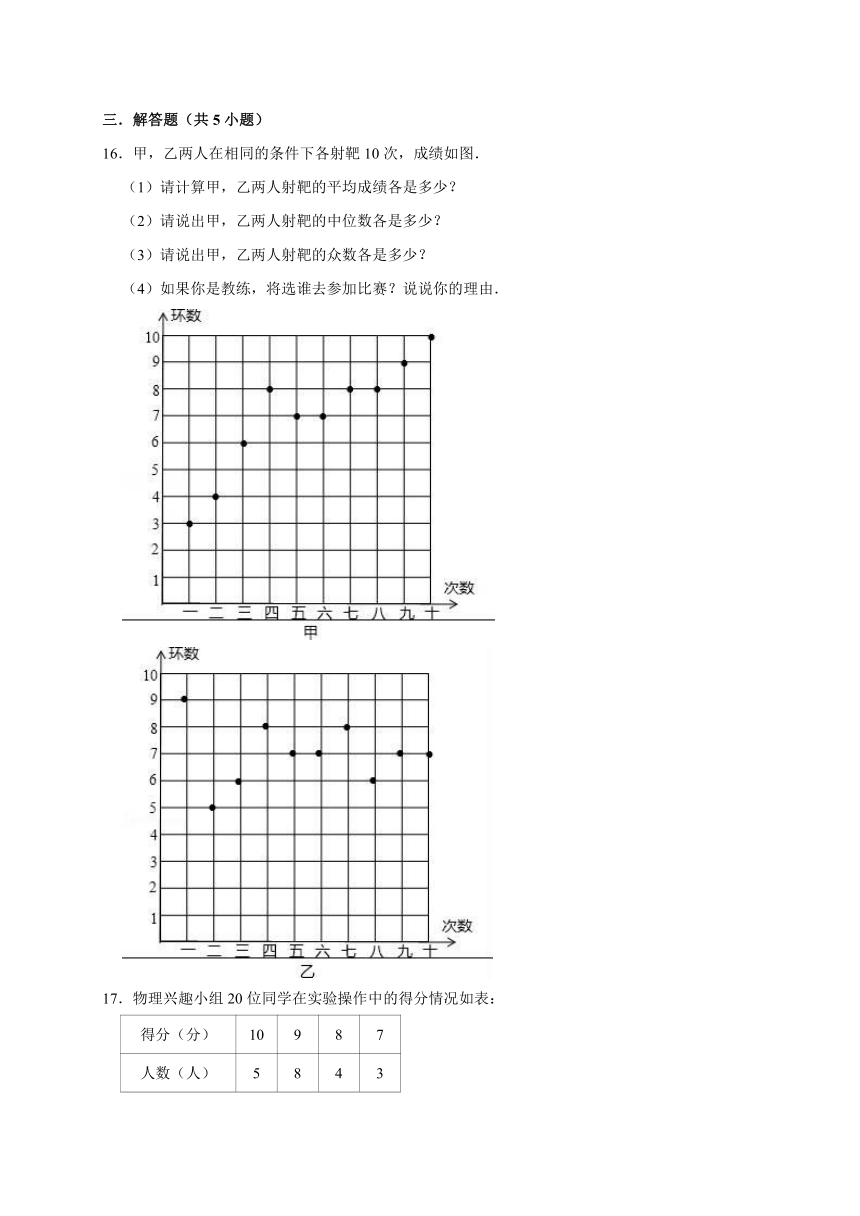
16.甲,乙两人在相同的条件下各射靶10次,成绩如图.
(1)请计算甲,乙两人射靶的平均成绩各是多少?
(2)请说出甲,乙两人射靶的中位数各是多少?
(3)请说出甲,乙两人射靶的众数各是多少?
(4)如果你是教练,将选谁去参加比赛?说说你的理由.
17.物理兴趣小组20位同学在实验操作中的得分情况如表:
得分(分) 10 9 8 7
人数(人) 5 8 4 3
①求这20位同学实验操作得分的众数、中位数.
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
18.体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
19.某公司10名销售员,去年完成的销售额情况如表:
销售额(单位:万元) 3 4 5 6 7 8 10
销售员人数(单位:人) 1 3 2 1 1 1 1
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元?
20.芜湖市1985年~2008年各年度专利数一览表
年度 专利数 年度 专利数 年度 专利数 年度 专利数
1985 0 1991 21 1997 56 2003 138
1986 2 1992 27 1998 55 2004 165
1987 3 1993 32 1999 110 2005 184
1988 8 1994 22 2000 71 2006 194
1989 9 1995 19 2001 60 2007 702
1990 13 1996 36 2002 71 2008 1006
(1)请你根据以上专利数数据,求出该组数据的中位数为 ;极差为 ;
(2)请用折线图描述2001年~2008年各年度的专利数;
(3)请你根据这组数据,说出你得到的信息.
2019年人教版八下数学《第20章 数据的分析》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.【分析】根据数据a1+1,a2+2,a3+3,a4+4,a5+5比数据a1、a2、a3、a4、a5的和多15,可得数据a1+1,a2+2,a3+3,a4+4,a5+5的平均数比a多3,据此求解即可.
【解答】解:a+[(a1+1+a2+2+a3+3+a4+4+a5+5)﹣(a1+a2+a3+a4+a5)]÷5
=a+[1+2+3+4+5]÷5
=a+15÷5
=a+3
故选:B.
【点评】此题主要考查了算术平均数的含义和求法,要熟练掌握,解答此题的关键是判断出:数据a1+1,a2+2,a3+3,a4+4,a5+5比数据a1、a2、a3、a4、a5的平均数多3.
2.【分析】本题需先根据要求的数分别列出式子,再根据x1,x2,x3,x4,x5的平均数是x,把它代入所求的式子,即可求出正确答案.
【解答】解:这组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是:
(2x1+5+2x2+5+2x3+5+2x4+5+2x5+5)÷5
=[(2x1+2x2+2x3+2x4+2x5)+(5+5+5+5+5)]÷5
=[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5
根据x1,x2,x3,x4,x5的平均数是x,
∴(x1+x2+x3+x4+x5)÷5=x,
∴x1+x2+x3+x4+x5=5x,
把x1+x2+x3+x4+x5=5x代入[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5得;
=(10x+25)÷5,
=2x+5.
故选:C.
【点评】本题主要考查了算术平均数,在解题时要根据算术平均数的定义,再结合所给的条件是解本题的关键.
3.【分析】设男、女生的人数分别为x、y,根据加权平均数的概念列式整理即可得解.
【解答】解:设男、女生的人数分别为x、y,
82x+77y=80(x+y),
整理得,2x=3y,
所以,x:y=3:2.
故选:C.
【点评】本题考查了加权平均数的求法,熟记定义是解题的关键.
4.【分析】只要运用加权平均数的公式即可求出,为简单题.
【解答】解:平均用电=(45×3+50×5+42×6)÷(3+5+6)=45.5度.
故选:C.
【点评】本题考查了平均数的定义.一组数据的平均数等于所有数据的和除以数据的个数.
5.【分析】利用中位数及平均数的定义求解即可.
【解答】解:按从小到大的顺序排列数为22,22,24,26,26,26,29,由中位数的定义可得:这组数据的中位数是26,
这组数据的平均数分别是=25,
故选:D.
【点评】本题主要考查了中位数与加权平均数,解题的关键是熟记中位数与加权平均数的定义.
6.【分析】因为中位数的值与大小排列顺序有关,而此题中x的大小位置未定,故应该分类讨论x所处的所有位置情况:从小到大(或从大到小)排列在中间(在第二位或第三位结果不影响);结尾;开始的位置.
【解答】解:(1)将这组数据从大到小的顺序排列为10,8,x,6,
处于中间位置的数是8,x,
那么由中位数的定义可知,这组数据的中位数是(8+x)÷2,
平均数为(10+8+x+6)÷4,
∵数据10,8,x,6,的中位数与平均数相等,
∴(8+x)÷2=(10+8+x+6)÷4,
解得x=8,大小位置与8对调,不影响结果,符合题意;
(2)将这组数据从大到小的顺序排列后10,8,6,x,
中位数是(8+6)÷2=7,
此时平均数是(10+8+x+6)÷4=7,
解得x=4,符合排列顺序;
(3)将这组数据从大到小的顺序排列后x,10,8,6,
中位数是(10+8)÷2=9,
平均数(10+8+x+6)÷4=9,
解得x=12,符合排列顺序.
∴x的值为4、8或12.
故选:C.
【点评】本题结合平均数考查了确定一组数据的中位数的能力.涉及到分类讨论思想,较难,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
7.【分析】一组数据中出现次数最多的数为众数;
将这组数据从小到大的顺序排列,处于中间位置的一个数或两个数的平均数是中位数.
根据平均数的定义求解.
【解答】解:在这一组数据中4是出现次数最多的,故众数是4;
将这组数据已经从小到大的顺序排列,处于中间位置的那个数是4,那么由中位数的定义可知,这组数据的中位数是4;
由平均数的公式的,=(3+4+4+6+8)÷5=5,平均数为5,
故选:C.
【点评】本题为统计题,考查平均数、众数与中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
8.【分析】根据众数和中位数的定义,出现次数最多的那个数就是众数,把一组数据按照大小顺序排列,中间那个数或中间两个数的平均数叫中位数.
【解答】解:捐款30元的人数为20人,最多,则众数为30,
中间两个数分别为30和30,则中位数是30,
故选:C.
【点评】本题考查了条形统计图、众数和中位数,这是基础知识要熟练掌握.
9.【分析】根据极差、平均数、中位数、众数的概念求解.
【解答】解:这组数据按照从小到大的顺序排列为:25,30,30,40,40,40,40,50,50,60,
极差为:60﹣25=35,
众数为:40,
中位数为:40,
平均数为:=40.5.
故选:C.
【点评】本题考查了极差、平均数、中位数、众数的知识,解答本题的关键是掌握各知识点的概念.
10.【分析】根据极差、中位数、众数及平均数的定义,结合数据进行分析即可.
【解答】解:将数据从小到大排列为:78,85,91,98,98,
A、极差为98﹣78=20,说法正确,故本选项错误;
B、中位数是91,说法正确,故本选项错误;
C、众数是98,说法正确,故本选项错误;
D、平均数是=90,说法错误,故本选项正确;
故选:D.
【点评】本题考查了极差、中位数、众数及平均数的知识,属于基础题,解答本题的关键是掌握各部分的定义.
二.填空题(共5小题)
11.【分析】根据中位数找法,分两三情况讨论:①x最小;②x最大;③80≤x≤100.然后列方程,解方程即可.
【解答】解:①x最小时,这组数据为x,x,80,100,100;中位数是80,
∴(100+100+x+x+80)÷5=80,
∴x=60;
②x最大时,这组数据为80,100,100,x,x;中位数是100,
∴(100+100+x+x+80)÷5=100,
∴x=110.
③当80≤x≤100,这组数据为80,x,x,100,100;中位数是x.
∴(100+100+x+x+80)÷5=x,
∴x=,x不是整数,舍去.
故答案为:60或110.
【点评】本题考查了平均数和中位数的定义.正确运用分类讨论的思想是解答本题的关键.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
12.【分析】根据加权平均数的计算公式求解即可.
【解答】解:该班卫生检查的总成绩=85×30%+90×40%+95×30%=90(分).
故答案为90分.
【点评】本题考查的是加权平均数的求法.本题易出现的错误是求85,90,95这三个数的平均数,对平均数的理解不正确.
13.【分析】运用平均数的意义求解.两组数据的总和相差88﹣8=80,则它们的平均数相差80÷20.
【解答】解:由题意知,将88误输入为8,则总和将少加(88﹣8)=80,所以算出的平均数比实际的平均数少80÷20=4.
故答案为:4.
【点评】本题考查了平均数的概念.熟记公式是解决本题的关键.
14.【分析】因为一组数据:25,29,20,x,14,它的中位数是24,则这组数据为14,20,23,25,29,所以其平均数可求.
【解答】解:∵一组数据:25,29,20,x,14,它的中位数是24,所以x=24,
∴这组数据为14,20,24,25,29,
∴平均数=(14+20+24+25+29)÷5=22.4.
故答案是:22.4.
【点评】本题考查了中位数,算术平均数.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
15.【分析】根据众数和平均数的概念结合图形分别求解即可.
【解答】解:由图可看出年收入2400的有50户,出现的次数最多,故众数是2400(元);
年收入的平均数==2080(元)
故填2400,2080.
【点评】此题主要考查学生对众数及平均数的概念的理解及实际运用能力.
三.解答题(共5小题)
16.【分析】根据平均数、中位数和众数的定义求解.
【解答】解:由图中的数据可得,甲,乙的平均成绩均为7环;分别将两人的射靶数按从小到大的顺序排列得到其中位数分别为7.5,7;可以看出甲射的8环的有三次,乙射7环有四次,所以其众数分别为8,7;甲有5次是8环以上的,而乙只有3次是8环以上的,所以应该选甲去.
答:(1)甲,乙两人射靶的平均成绩各是7环,7环;
(2)甲,乙两人射靶的中位数各是7.5,7;
(3)甲,乙两人射靶的众数各是8,7;
(4)选甲去,理由:甲有5次是8环以上的,而乙只有3次是8环以上的.
【点评】此题考查学生对平均数,中位数及众数的理解及实际应用能力.
17.【分析】①得9分的有8人,频数最多;20个数据的中位数是第10个和第11个同学的得分的平均数.
②平均分=总分数÷总人数.
③扇形①的圆心角=百分比×360°
【解答】解:①得9分的有8人,频数最多;20个数据的中位数是第10个和第11个同学的得分的平均数即(9+9)÷2=9.
所以众数为9,中位数为9.
②平均分=分;
③圆心角度数=(1﹣25%﹣40%﹣20%)×360°=54°.
【点评】本题用到的知识点是:给定一组数据,出现次数最多的那个数,称为这组数据的众数.中位数的定义:将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.平均数=总数÷个数.扇形的圆心角=扇形百分比×360度.
18.【分析】(1)利用条形统计图得出进球总数,进而得出平均数和中位数;
(2)利用样本中优秀率,再估计总体优秀人数.
【解答】解:(1)由条形统计图可得,女生进球数的平均数为:(1×1+2×4+1×3+4×2)÷8=2.5(个);
∵第4,5个数据都是2,则其平均数为:2;
∴女生进球数的中位数为:2,
(2)样本中优秀率为:,
故全校有女生1200人,“优秀”等级的女生为:1200×=450(人),
答:“优秀”等级的女生约为450人.
【点评】此题主要考查了中位数以及利用样本估计总体和算术平均数求法,正确掌握中位数的定义是解题关键.
19.【分析】(1)根据平均数公式求得平均数,根据次数出现最多的数确定众数,按从小到大顺序排列好后求得中位数.
(2)根据平均数,中位数,众数的意义回答.
【解答】解:
(1)平均数=(3×1+4×3+5×2+6×1+7×1+8×1+10×1)=5.6(万元);
出现次数最多的是4万元,所以众数是4(万元);
因为第五,第六个数均是5万元,所以中位数是5(万元).
(2)今年每个销售人员统一的销售标准应是5万元.
理由如下:若规定平均数5.6万元为标准,则多数人无法或不可能超额完成,会挫伤员工的积极性;若规定众数4万元为标准,则大多数人不必努力就可以超额完成,不利于提高年销售额;若规定中位数5万元为标准,则大多数人能完成或超额完成,少数人经过努力也能完成.因此把5万元定为标准比较合理.
【点评】本题为众数,中位数,平均数的意义.解题的关键是根据众数,中位数,平均数的意义求出答案.
20.【分析】(1)利用中位数和极差的概念即可求解;
(2)根据画折线图的具体步骤画图即可;
(3)开放性题目,根据图中所获信息,描述合理即可.
【解答】解:
(1)中位数为46,极差为1006;
(2)如图:
(3)芜湖的专利数从无到有,近几年专利数增加迅速.(必须围绕专利数据来谈)
【点评】数据中最大的数减去最小的数即为极差;对于中位数;因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可;画折线图可用描点法画图.
一.选择题(共10小题)
1.已知5个数a1、a2、a3、a4、a5的平均数是a,则数据a1+1,a2+2,a3+3,a4+4,a5+5的平均数为( )
A.a B.a+3 C. a D.a+15
2.一组数据x1,x2,x3,x4,x5的平均数是x,另一组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是( )
A.x B.2x C.2x+5 D.10x+25
3.某中学初三(1)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男、女生的人数之比为( )
A.1:2 B.2:1 C.3:2 D.2:3
4.某居民区的月底统计用电情况如下,其中3户用电45度,5户用电50度,6户用电42度,则平均用电( )度.
A.41 B.42 C.45.5 D.46
5.本市5月份某一周每天的最高气温统计如下表:
温度/℃ 22 24 26 29
天数 2 1 3 1
则这组数据的中位数和平均数分别是( )
A.24,25 B.25,26 C.26,24 D.26,25
6.已知一组数据6,8,10,x的中位数与平均数相等,这样的x有( )
A.1个 B.2个
C.3个 D.4个以上(含4个)
7.在一组数据3,4,4,6,8中,下列说法错误的是( )
A.它的众数是4 B.它的平均数是5
C.它的中位数是5 D.它的众数等于中位数
8.抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
A.20,20 B.30,20 C.30,30 D.20,30
9.为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表,关于这10户家庭的月用电量说法正确的是( )
月用电量(度) 25 30 40 50 60
户数 1 2 4 2 1
A.极差是3 B.众数是4
C.中位数40 D.平均数是20.5
10.一次数学测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85,98.关于这组数据说法错误的是( )
A.极差是20 B.中位数是91 C.众数是98 D.平均数是91
二.填空题(共5小题)
11.小明等五名同学四月份参加某次数学测验的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为 .
12.在学校的卫生检查中,规定各班的教室卫生成绩占30%,环境卫生成绩占40%,个人卫生成绩占30%.八年级一班这三项成绩分别为85分,90分和95分,求该班卫生检查的总成绩 .
13.某同学在使用计算器求20个数的时候,将88误输入为8,那么由此求出的平均数与实际平均数的差为 .
14.一组数据:25,29,20,x,14,它的中位数是24,则这组数据的平均数为 .
15.某学习小组,对我市居民家庭年收入进行调查,并将数据绘制成图,家庭年收入的众数为 元;这些家庭年收入的平均数为 元.
三.解答题(共5小题)
16.甲,乙两人在相同的条件下各射靶10次,成绩如图.
(1)请计算甲,乙两人射靶的平均成绩各是多少?
(2)请说出甲,乙两人射靶的中位数各是多少?
(3)请说出甲,乙两人射靶的众数各是多少?
(4)如果你是教练,将选谁去参加比赛?说说你的理由.
17.物理兴趣小组20位同学在实验操作中的得分情况如表:
得分(分) 10 9 8 7
人数(人) 5 8 4 3
①求这20位同学实验操作得分的众数、中位数.
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
18.体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
19.某公司10名销售员,去年完成的销售额情况如表:
销售额(单位:万元) 3 4 5 6 7 8 10
销售员人数(单位:人) 1 3 2 1 1 1 1
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元?
20.芜湖市1985年~2008年各年度专利数一览表
年度 专利数 年度 专利数 年度 专利数 年度 专利数
1985 0 1991 21 1997 56 2003 138
1986 2 1992 27 1998 55 2004 165
1987 3 1993 32 1999 110 2005 184
1988 8 1994 22 2000 71 2006 194
1989 9 1995 19 2001 60 2007 702
1990 13 1996 36 2002 71 2008 1006
(1)请你根据以上专利数数据,求出该组数据的中位数为 ;极差为 ;
(2)请用折线图描述2001年~2008年各年度的专利数;
(3)请你根据这组数据,说出你得到的信息.
2019年人教版八下数学《第20章 数据的分析》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.【分析】根据数据a1+1,a2+2,a3+3,a4+4,a5+5比数据a1、a2、a3、a4、a5的和多15,可得数据a1+1,a2+2,a3+3,a4+4,a5+5的平均数比a多3,据此求解即可.
【解答】解:a+[(a1+1+a2+2+a3+3+a4+4+a5+5)﹣(a1+a2+a3+a4+a5)]÷5
=a+[1+2+3+4+5]÷5
=a+15÷5
=a+3
故选:B.
【点评】此题主要考查了算术平均数的含义和求法,要熟练掌握,解答此题的关键是判断出:数据a1+1,a2+2,a3+3,a4+4,a5+5比数据a1、a2、a3、a4、a5的平均数多3.
2.【分析】本题需先根据要求的数分别列出式子,再根据x1,x2,x3,x4,x5的平均数是x,把它代入所求的式子,即可求出正确答案.
【解答】解:这组数据2x1+5,2x2+5,2x3+5,2x4+5,2x5+5的平均数是:
(2x1+5+2x2+5+2x3+5+2x4+5+2x5+5)÷5
=[(2x1+2x2+2x3+2x4+2x5)+(5+5+5+5+5)]÷5
=[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5
根据x1,x2,x3,x4,x5的平均数是x,
∴(x1+x2+x3+x4+x5)÷5=x,
∴x1+x2+x3+x4+x5=5x,
把x1+x2+x3+x4+x5=5x代入[2(x1+x2+x3+x4+x5)+(5+5+5+5+5)]÷5得;
=(10x+25)÷5,
=2x+5.
故选:C.
【点评】本题主要考查了算术平均数,在解题时要根据算术平均数的定义,再结合所给的条件是解本题的关键.
3.【分析】设男、女生的人数分别为x、y,根据加权平均数的概念列式整理即可得解.
【解答】解:设男、女生的人数分别为x、y,
82x+77y=80(x+y),
整理得,2x=3y,
所以,x:y=3:2.
故选:C.
【点评】本题考查了加权平均数的求法,熟记定义是解题的关键.
4.【分析】只要运用加权平均数的公式即可求出,为简单题.
【解答】解:平均用电=(45×3+50×5+42×6)÷(3+5+6)=45.5度.
故选:C.
【点评】本题考查了平均数的定义.一组数据的平均数等于所有数据的和除以数据的个数.
5.【分析】利用中位数及平均数的定义求解即可.
【解答】解:按从小到大的顺序排列数为22,22,24,26,26,26,29,由中位数的定义可得:这组数据的中位数是26,
这组数据的平均数分别是=25,
故选:D.
【点评】本题主要考查了中位数与加权平均数,解题的关键是熟记中位数与加权平均数的定义.
6.【分析】因为中位数的值与大小排列顺序有关,而此题中x的大小位置未定,故应该分类讨论x所处的所有位置情况:从小到大(或从大到小)排列在中间(在第二位或第三位结果不影响);结尾;开始的位置.
【解答】解:(1)将这组数据从大到小的顺序排列为10,8,x,6,
处于中间位置的数是8,x,
那么由中位数的定义可知,这组数据的中位数是(8+x)÷2,
平均数为(10+8+x+6)÷4,
∵数据10,8,x,6,的中位数与平均数相等,
∴(8+x)÷2=(10+8+x+6)÷4,
解得x=8,大小位置与8对调,不影响结果,符合题意;
(2)将这组数据从大到小的顺序排列后10,8,6,x,
中位数是(8+6)÷2=7,
此时平均数是(10+8+x+6)÷4=7,
解得x=4,符合排列顺序;
(3)将这组数据从大到小的顺序排列后x,10,8,6,
中位数是(10+8)÷2=9,
平均数(10+8+x+6)÷4=9,
解得x=12,符合排列顺序.
∴x的值为4、8或12.
故选:C.
【点评】本题结合平均数考查了确定一组数据的中位数的能力.涉及到分类讨论思想,较难,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
7.【分析】一组数据中出现次数最多的数为众数;
将这组数据从小到大的顺序排列,处于中间位置的一个数或两个数的平均数是中位数.
根据平均数的定义求解.
【解答】解:在这一组数据中4是出现次数最多的,故众数是4;
将这组数据已经从小到大的顺序排列,处于中间位置的那个数是4,那么由中位数的定义可知,这组数据的中位数是4;
由平均数的公式的,=(3+4+4+6+8)÷5=5,平均数为5,
故选:C.
【点评】本题为统计题,考查平均数、众数与中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
8.【分析】根据众数和中位数的定义,出现次数最多的那个数就是众数,把一组数据按照大小顺序排列,中间那个数或中间两个数的平均数叫中位数.
【解答】解:捐款30元的人数为20人,最多,则众数为30,
中间两个数分别为30和30,则中位数是30,
故选:C.
【点评】本题考查了条形统计图、众数和中位数,这是基础知识要熟练掌握.
9.【分析】根据极差、平均数、中位数、众数的概念求解.
【解答】解:这组数据按照从小到大的顺序排列为:25,30,30,40,40,40,40,50,50,60,
极差为:60﹣25=35,
众数为:40,
中位数为:40,
平均数为:=40.5.
故选:C.
【点评】本题考查了极差、平均数、中位数、众数的知识,解答本题的关键是掌握各知识点的概念.
10.【分析】根据极差、中位数、众数及平均数的定义,结合数据进行分析即可.
【解答】解:将数据从小到大排列为:78,85,91,98,98,
A、极差为98﹣78=20,说法正确,故本选项错误;
B、中位数是91,说法正确,故本选项错误;
C、众数是98,说法正确,故本选项错误;
D、平均数是=90,说法错误,故本选项正确;
故选:D.
【点评】本题考查了极差、中位数、众数及平均数的知识,属于基础题,解答本题的关键是掌握各部分的定义.
二.填空题(共5小题)
11.【分析】根据中位数找法,分两三情况讨论:①x最小;②x最大;③80≤x≤100.然后列方程,解方程即可.
【解答】解:①x最小时,这组数据为x,x,80,100,100;中位数是80,
∴(100+100+x+x+80)÷5=80,
∴x=60;
②x最大时,这组数据为80,100,100,x,x;中位数是100,
∴(100+100+x+x+80)÷5=100,
∴x=110.
③当80≤x≤100,这组数据为80,x,x,100,100;中位数是x.
∴(100+100+x+x+80)÷5=x,
∴x=,x不是整数,舍去.
故答案为:60或110.
【点评】本题考查了平均数和中位数的定义.正确运用分类讨论的思想是解答本题的关键.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
12.【分析】根据加权平均数的计算公式求解即可.
【解答】解:该班卫生检查的总成绩=85×30%+90×40%+95×30%=90(分).
故答案为90分.
【点评】本题考查的是加权平均数的求法.本题易出现的错误是求85,90,95这三个数的平均数,对平均数的理解不正确.
13.【分析】运用平均数的意义求解.两组数据的总和相差88﹣8=80,则它们的平均数相差80÷20.
【解答】解:由题意知,将88误输入为8,则总和将少加(88﹣8)=80,所以算出的平均数比实际的平均数少80÷20=4.
故答案为:4.
【点评】本题考查了平均数的概念.熟记公式是解决本题的关键.
14.【分析】因为一组数据:25,29,20,x,14,它的中位数是24,则这组数据为14,20,23,25,29,所以其平均数可求.
【解答】解:∵一组数据:25,29,20,x,14,它的中位数是24,所以x=24,
∴这组数据为14,20,24,25,29,
∴平均数=(14+20+24+25+29)÷5=22.4.
故答案是:22.4.
【点评】本题考查了中位数,算术平均数.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
15.【分析】根据众数和平均数的概念结合图形分别求解即可.
【解答】解:由图可看出年收入2400的有50户,出现的次数最多,故众数是2400(元);
年收入的平均数==2080(元)
故填2400,2080.
【点评】此题主要考查学生对众数及平均数的概念的理解及实际运用能力.
三.解答题(共5小题)
16.【分析】根据平均数、中位数和众数的定义求解.
【解答】解:由图中的数据可得,甲,乙的平均成绩均为7环;分别将两人的射靶数按从小到大的顺序排列得到其中位数分别为7.5,7;可以看出甲射的8环的有三次,乙射7环有四次,所以其众数分别为8,7;甲有5次是8环以上的,而乙只有3次是8环以上的,所以应该选甲去.
答:(1)甲,乙两人射靶的平均成绩各是7环,7环;
(2)甲,乙两人射靶的中位数各是7.5,7;
(3)甲,乙两人射靶的众数各是8,7;
(4)选甲去,理由:甲有5次是8环以上的,而乙只有3次是8环以上的.
【点评】此题考查学生对平均数,中位数及众数的理解及实际应用能力.
17.【分析】①得9分的有8人,频数最多;20个数据的中位数是第10个和第11个同学的得分的平均数.
②平均分=总分数÷总人数.
③扇形①的圆心角=百分比×360°
【解答】解:①得9分的有8人,频数最多;20个数据的中位数是第10个和第11个同学的得分的平均数即(9+9)÷2=9.
所以众数为9,中位数为9.
②平均分=分;
③圆心角度数=(1﹣25%﹣40%﹣20%)×360°=54°.
【点评】本题用到的知识点是:给定一组数据,出现次数最多的那个数,称为这组数据的众数.中位数的定义:将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.平均数=总数÷个数.扇形的圆心角=扇形百分比×360度.
18.【分析】(1)利用条形统计图得出进球总数,进而得出平均数和中位数;
(2)利用样本中优秀率,再估计总体优秀人数.
【解答】解:(1)由条形统计图可得,女生进球数的平均数为:(1×1+2×4+1×3+4×2)÷8=2.5(个);
∵第4,5个数据都是2,则其平均数为:2;
∴女生进球数的中位数为:2,
(2)样本中优秀率为:,
故全校有女生1200人,“优秀”等级的女生为:1200×=450(人),
答:“优秀”等级的女生约为450人.
【点评】此题主要考查了中位数以及利用样本估计总体和算术平均数求法,正确掌握中位数的定义是解题关键.
19.【分析】(1)根据平均数公式求得平均数,根据次数出现最多的数确定众数,按从小到大顺序排列好后求得中位数.
(2)根据平均数,中位数,众数的意义回答.
【解答】解:
(1)平均数=(3×1+4×3+5×2+6×1+7×1+8×1+10×1)=5.6(万元);
出现次数最多的是4万元,所以众数是4(万元);
因为第五,第六个数均是5万元,所以中位数是5(万元).
(2)今年每个销售人员统一的销售标准应是5万元.
理由如下:若规定平均数5.6万元为标准,则多数人无法或不可能超额完成,会挫伤员工的积极性;若规定众数4万元为标准,则大多数人不必努力就可以超额完成,不利于提高年销售额;若规定中位数5万元为标准,则大多数人能完成或超额完成,少数人经过努力也能完成.因此把5万元定为标准比较合理.
【点评】本题为众数,中位数,平均数的意义.解题的关键是根据众数,中位数,平均数的意义求出答案.
20.【分析】(1)利用中位数和极差的概念即可求解;
(2)根据画折线图的具体步骤画图即可;
(3)开放性题目,根据图中所获信息,描述合理即可.
【解答】解:
(1)中位数为46,极差为1006;
(2)如图:
(3)芜湖的专利数从无到有,近几年专利数增加迅速.(必须围绕专利数据来谈)
【点评】数据中最大的数减去最小的数即为极差;对于中位数;因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可;画折线图可用描点法画图.
