江苏省东台市创新高级中学2018-2019学年高一下学期3月月考数学试题 Word版含答案
文档属性
| 名称 | 江苏省东台市创新高级中学2018-2019学年高一下学期3月月考数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 212.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-28 16:15:52 | ||
图片预览


文档简介
东台创新高级中学2018-2019学年度第二学期
2018级数学3月份检测试卷
(考试时间:120分钟 满分:150分)
选择题:本大题共12小题,每小题5分,共60分。请把答案涂在答题卡相应位置上。
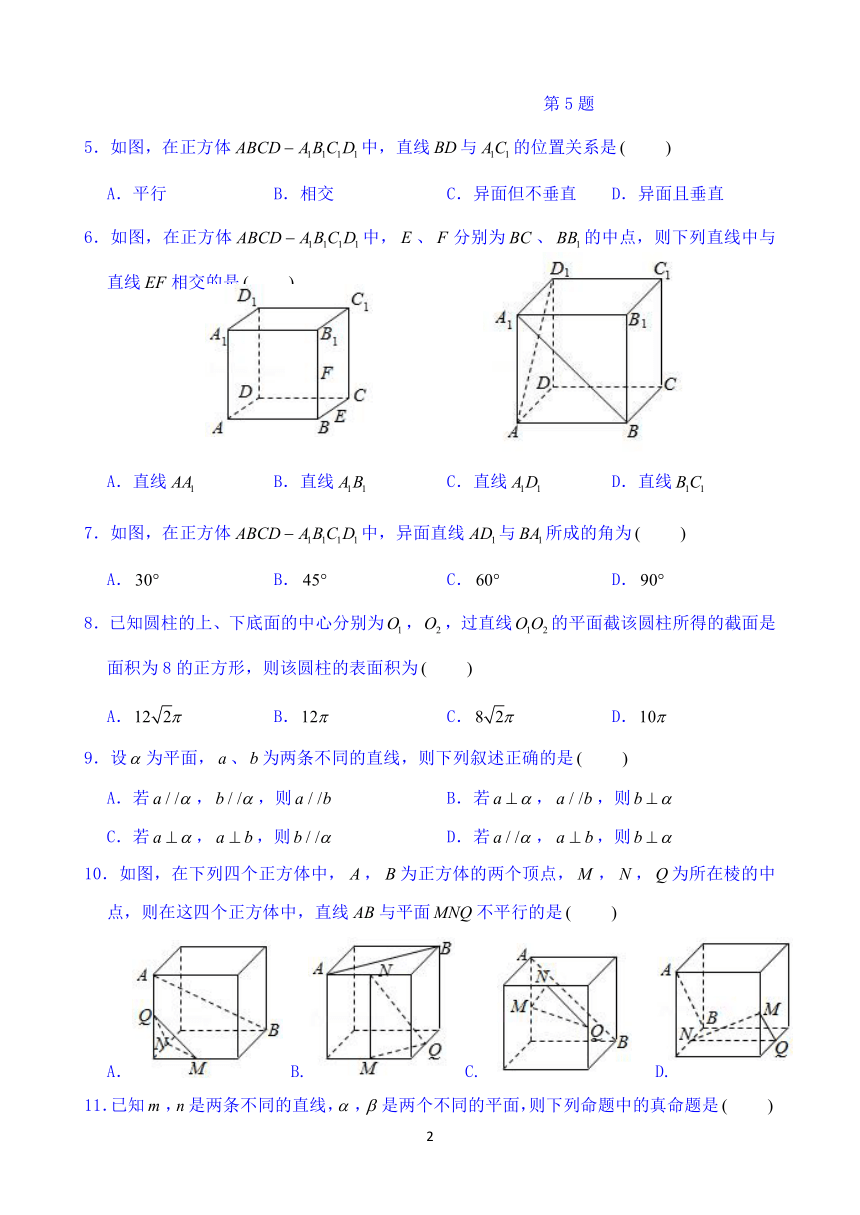
1.已知直线经过两点,,那么直线的斜率为
A. B. C. D.3
2.如图是由哪个平面图形旋转得到的
A. B. C. D.
3.给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;
③在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;
④圆柱的任意两条母线所在的直线是互相平行的.
其中正确的是
A.①② B.②③ C.①③ D.②④
4.下列说法中正确的是
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有的几何体的表面都能展成平面图形
D.棱柱的各条棱都相等
第5题
5.如图,在正方体中,直线与的位置关系是
A.平行 B.相交 C.异面但不垂直 D.异面且垂直
6.如图,在正方体中,、分别为、的中点,则下列直线中与直线相交的是
A.直线 B.直线 C.直线 D.直线
7.如图,在正方体中,异面直线与所成的角为
A. B. C. D.
8.已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为
A. B. C. D.
9.设为平面,、为两条不同的直线,则下列叙述正确的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
10.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是
A. B. C. D.
11.已知,是两条不同的直线,,是两个不同的平面,则下列命题中的真命题是
A.若,,,则 B.若,,,则
C.若,,,则 D.若,,,则
12.三棱锥中,平面,,,,则该三棱锥外接球的表面积为
A. B. C. D.
填空题:本大题共4小题,每小题5分,共20分。请把答案填在答题纸相应位置上。
13.直线的倾斜角是 .
14.设圆锥的轴截面是一个边长为的正三角形,则该圆锥的体积为 .
15.已知正三棱柱的各梭长均为2.点在棱上,则三棱锥的体积为 .
16.如图,在圆柱内有一个球,该球与圆柱的上、下底面及母线均相切,记圆柱的体积为,球的体积为,则的值是
解答题:本大题共6小题,共计70分,请在答题纸指定区域答题.
17.(本小题满分10分)
已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61,
(1)求a与b的夹角θ;
(2)求|a+2b|;
18.(本小题满分12分)
已知函数f(x)=(sin x+cos x)2+2cos2x-2.
(1)求f(x)的单调递增区间;
(2)当时,求函数f(x)的最大值和最小值.
19.(本小题满分10分)
如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.
(1)求证:MN∥平面BCD;
(2)求证:平面ABC⊥平面ACD.
20.(本小题满分12分)
如图,在正三棱柱ABC﹣A1B1C1中,D为AB的中点.
(1) 求证:CD⊥平面ABB1A1;
(2) 求证:BC1∥平面A1CD.
21.(本小题满分12分)
如图,在四棱锥中,M,N分别为棱PA,PD的中点.已知侧面PAD⊥底面ABCD,底面ABCD是矩形,DA=DP.
求证:(1)MN∥平面PBC;
(2)MD⊥平面PAB.
22.(本小题满分12分)
如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PD⊥平面ABCD.
(1)求证:AD⊥PC;
(2)若E是BC的中点,F在PC上,PA∥平面DEF,求的值.
东台创新高级中学2018-2019学年度第二学期
2018级数学3月份检测试卷参考答案
一.选择题:每题5分,共60分。
1
2
3
4
5
6
C
D
D
B
D
D
7
8
9
10
11
12
C
B
B
A
D
A
二.填空题:每题5分,共20分。
三.解答题:共6题,共70分。
17.
18.
证明略。
2018级数学3月份检测试卷
(考试时间:120分钟 满分:150分)
选择题:本大题共12小题,每小题5分,共60分。请把答案涂在答题卡相应位置上。
1.已知直线经过两点,,那么直线的斜率为
A. B. C. D.3
2.如图是由哪个平面图形旋转得到的
A. B. C. D.
3.给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;
③在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;
④圆柱的任意两条母线所在的直线是互相平行的.
其中正确的是
A.①② B.②③ C.①③ D.②④
4.下列说法中正确的是
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有的几何体的表面都能展成平面图形
D.棱柱的各条棱都相等
第5题
5.如图,在正方体中,直线与的位置关系是
A.平行 B.相交 C.异面但不垂直 D.异面且垂直
6.如图,在正方体中,、分别为、的中点,则下列直线中与直线相交的是
A.直线 B.直线 C.直线 D.直线
7.如图,在正方体中,异面直线与所成的角为
A. B. C. D.
8.已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为
A. B. C. D.
9.设为平面,、为两条不同的直线,则下列叙述正确的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
10.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是
A. B. C. D.
11.已知,是两条不同的直线,,是两个不同的平面,则下列命题中的真命题是
A.若,,,则 B.若,,,则
C.若,,,则 D.若,,,则
12.三棱锥中,平面,,,,则该三棱锥外接球的表面积为
A. B. C. D.
填空题:本大题共4小题,每小题5分,共20分。请把答案填在答题纸相应位置上。
13.直线的倾斜角是 .
14.设圆锥的轴截面是一个边长为的正三角形,则该圆锥的体积为 .
15.已知正三棱柱的各梭长均为2.点在棱上,则三棱锥的体积为 .
16.如图,在圆柱内有一个球,该球与圆柱的上、下底面及母线均相切,记圆柱的体积为,球的体积为,则的值是
解答题:本大题共6小题,共计70分,请在答题纸指定区域答题.
17.(本小题满分10分)
已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61,
(1)求a与b的夹角θ;
(2)求|a+2b|;
18.(本小题满分12分)
已知函数f(x)=(sin x+cos x)2+2cos2x-2.
(1)求f(x)的单调递增区间;
(2)当时,求函数f(x)的最大值和最小值.
19.(本小题满分10分)
如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.
(1)求证:MN∥平面BCD;
(2)求证:平面ABC⊥平面ACD.
20.(本小题满分12分)
如图,在正三棱柱ABC﹣A1B1C1中,D为AB的中点.
(1) 求证:CD⊥平面ABB1A1;
(2) 求证:BC1∥平面A1CD.
21.(本小题满分12分)
如图,在四棱锥中,M,N分别为棱PA,PD的中点.已知侧面PAD⊥底面ABCD,底面ABCD是矩形,DA=DP.
求证:(1)MN∥平面PBC;
(2)MD⊥平面PAB.
22.(本小题满分12分)
如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PD⊥平面ABCD.
(1)求证:AD⊥PC;
(2)若E是BC的中点,F在PC上,PA∥平面DEF,求的值.
东台创新高级中学2018-2019学年度第二学期
2018级数学3月份检测试卷参考答案
一.选择题:每题5分,共60分。
1
2
3
4
5
6
C
D
D
B
D
D
7
8
9
10
11
12
C
B
B
A
D
A
二.填空题:每题5分,共20分。
三.解答题:共6题,共70分。
17.
18.
证明略。
同课章节目录
