华东师大版2019年春八年级数学下册19.2.2菱形的判定定理第2课时课件(20张PPT)
文档属性
| 名称 | 华东师大版2019年春八年级数学下册19.2.2菱形的判定定理第2课时课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 22:05:35 | ||
图片预览




文档简介
课件20张PPT。HS八(下)
教学课件第19章 矩形、菱形与主动性18.1 菱形2 菱形的判定第2课时 菱形的判定定理2学习目标1.利用菱形判定定理2来判断平行四边形是否为菱
形.(重点)
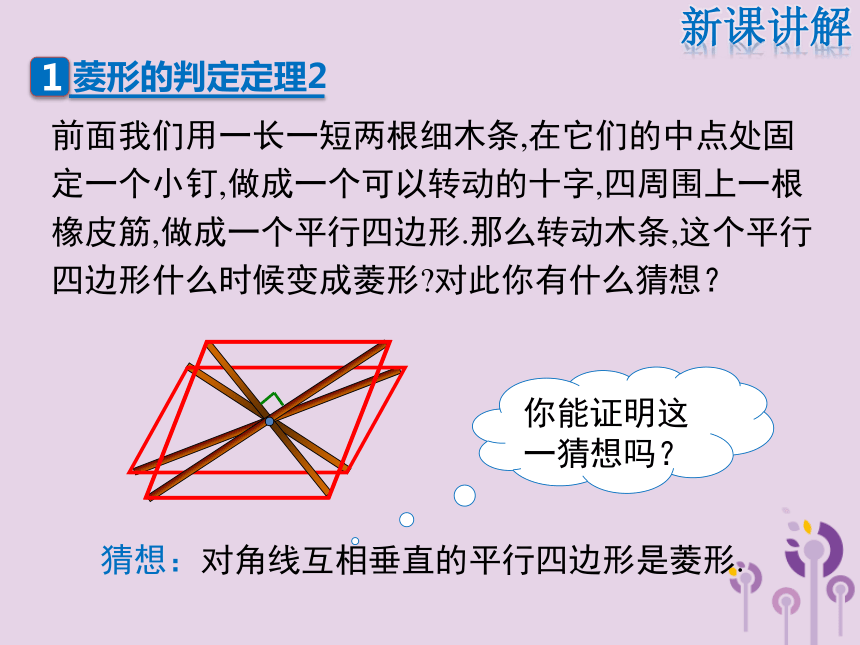
2.菱形的性质与判定的综合运用.(难点)上一课我们学习的菱形的判定方法有哪些?1.定义:有一组邻边相等的平行四边形叫做菱形.2.定理1:四边相等的四边形是菱形.菱形的特有性质:对角线互相垂直平分.对角线互相垂直平分的四边形是菱形.这个命题能作为判定菱形的定理吗?逆命题复习引入先将一张长方形的纸对折,再对折,然后沿图中的虚线剪下,将纸展开,就得到了一个菱形.(1)(2)(3)(4)你能说说这样做的道理吗?复习引入前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?猜想:对角线互相垂直的平行四边形是菱形.你能证明这一猜想吗?新课讲解菱形的判定定理2作一条两条对角线互相垂直的平行四边形.
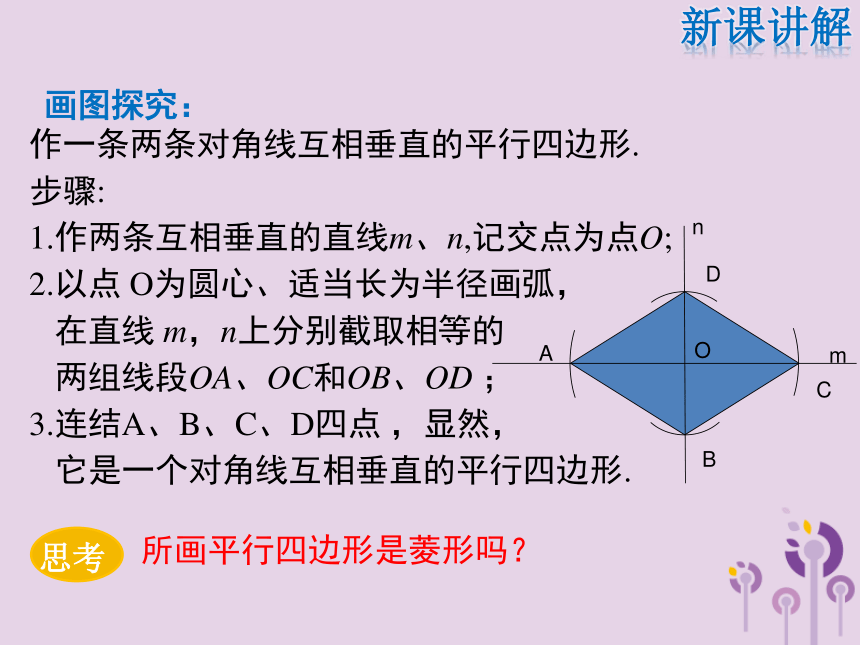
步骤:
1.作两条互相垂直的直线m、n,记交点为点O;
2.以点 O为圆心、适当长为半径画弧,
在直线 m,n上分别截取相等的
两组线段OA、OC和OB、OD ;
3.连结A、B、C、D四点 ,显然,
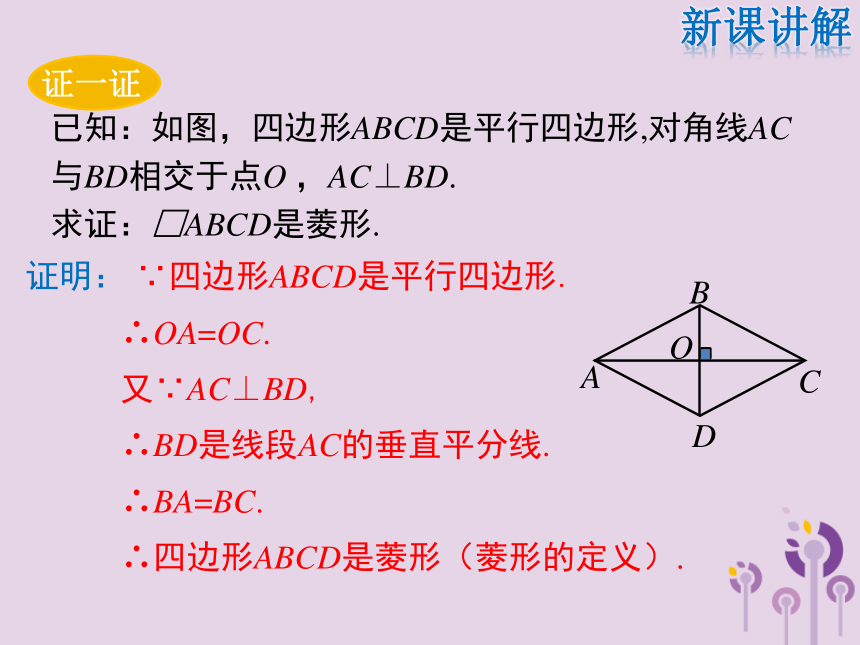
它是一个对角线互相垂直的平行四边形.所画平行四边形是菱形吗?O新课讲解画图探究:已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
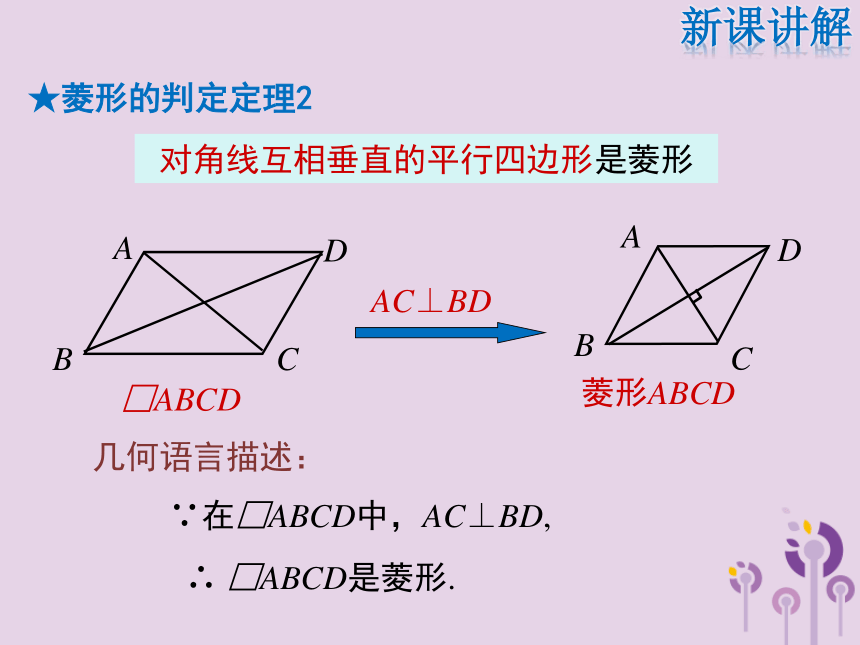
∴四边形ABCD是菱形(菱形的定义).新课讲解对角线互相垂直的平行四边形是菱形几何语言描述:
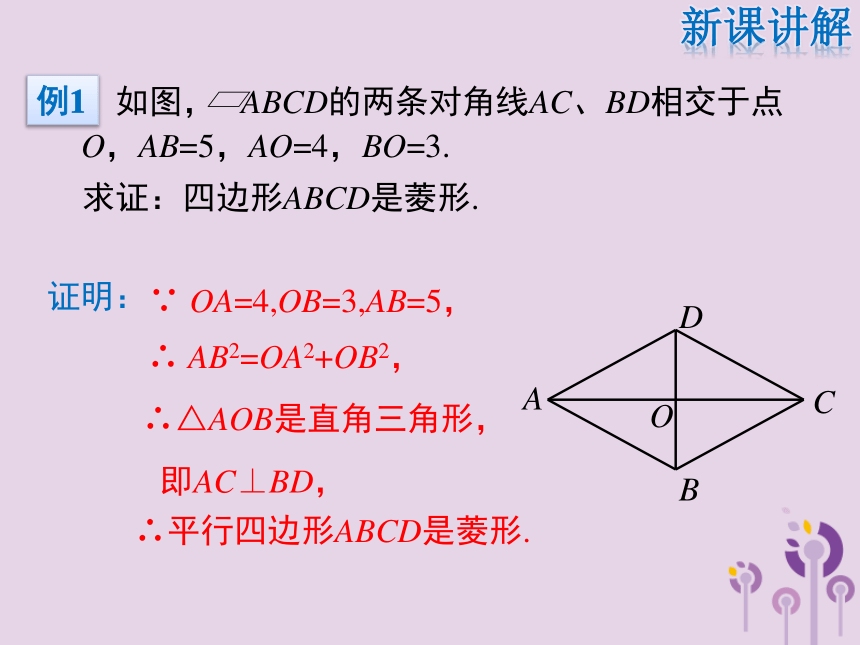
∵在□ABCD中,AC⊥BD,∴ □ABCD是菱形.新课讲解★菱形的判定定理2∴平行四边形ABCD是菱形.∵ OA=4,OB=3,AB=5,证明:即AC⊥BD,∴ AB2=OA2+OB2,∴△AOB是直角三角形,新课讲解例1 如图,矩形ABCD的对角线AC的垂直平分线与边AD、
BC分别交于点E、F,求证:四边形AFCE是菱形. ABCDEFO12证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∵∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.例2在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD B新课讲解 如图,在△ABC中,DE∥BC,且2DE=BC,BE=2DE,延长DE到点F,使得EF=BE,连结CF.
(1)求证:四边形BCFE是菱形;证明:∵DE∥BC,且2DE=BC,
BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形.新课讲解菱形的性质与判定的综合应用例3解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .(2)若CE=4,∠BCF=120°,求菱形BCFE的面积. 注意:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.新课讲解如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,求平行四边形ABCD的周长.解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,∠BAC=∠ACD.
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠ACD,
∴AD=DC,
∴四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.新课讲解1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形.
(2)对角线互相垂直且平分的四边形是菱形.
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形.
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.√ ╳ ╳ ╳ 2.一边长为5cm的平行四边形的两条对角线的长分别
为24cm和26cm,那么平行四边形的面积是 . 312cm2随堂即练3.如图,矩形ABCD的对角线相交于点O,DE∥AC,
CE ∥BD.求证:四边形OCED是菱形.证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形. 随堂即练4.如图,在平行四边形ABCD中,AC = 6,BD = 8,
AD = 5. 求AB的长.解: ∵ 四边形ABCD为平行四边形,∴ △DAO是直角三角形.∴ ∠DOA = 90°,即DB⊥AC.∴ 平行四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)∴ AB=AD=5 .随堂即练证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,
∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,
∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形. 5.如图,△ABC中,AC的垂直平分线MN交AB于点
D,交AC于点O,CE∥AB交MN于点E,连结AE、
CD.求证:四边形ADCE是菱形.BCN随堂即练四条边都相等菱形一组邻边相等对角线互相垂直对角线互相平分一组对边平行且相等两组对边分别平行或相等四边形平行四边形两组对角分别相等课堂总结
教学课件第19章 矩形、菱形与主动性18.1 菱形2 菱形的判定第2课时 菱形的判定定理2学习目标1.利用菱形判定定理2来判断平行四边形是否为菱
形.(重点)
2.菱形的性质与判定的综合运用.(难点)上一课我们学习的菱形的判定方法有哪些?1.定义:有一组邻边相等的平行四边形叫做菱形.2.定理1:四边相等的四边形是菱形.菱形的特有性质:对角线互相垂直平分.对角线互相垂直平分的四边形是菱形.这个命题能作为判定菱形的定理吗?逆命题复习引入先将一张长方形的纸对折,再对折,然后沿图中的虚线剪下,将纸展开,就得到了一个菱形.(1)(2)(3)(4)你能说说这样做的道理吗?复习引入前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?猜想:对角线互相垂直的平行四边形是菱形.你能证明这一猜想吗?新课讲解菱形的判定定理2作一条两条对角线互相垂直的平行四边形.
步骤:
1.作两条互相垂直的直线m、n,记交点为点O;
2.以点 O为圆心、适当长为半径画弧,
在直线 m,n上分别截取相等的
两组线段OA、OC和OB、OD ;
3.连结A、B、C、D四点 ,显然,
它是一个对角线互相垂直的平行四边形.所画平行四边形是菱形吗?O新课讲解画图探究:已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).新课讲解对角线互相垂直的平行四边形是菱形几何语言描述:
∵在□ABCD中,AC⊥BD,∴ □ABCD是菱形.新课讲解★菱形的判定定理2∴平行四边形ABCD是菱形.∵ OA=4,OB=3,AB=5,证明:即AC⊥BD,∴ AB2=OA2+OB2,∴△AOB是直角三角形,新课讲解例1 如图,矩形ABCD的对角线AC的垂直平分线与边AD、
BC分别交于点E、F,求证:四边形AFCE是菱形. ABCDEFO12证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∵∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.例2在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD B新课讲解 如图,在△ABC中,DE∥BC,且2DE=BC,BE=2DE,延长DE到点F,使得EF=BE,连结CF.
(1)求证:四边形BCFE是菱形;证明:∵DE∥BC,且2DE=BC,
BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形.新课讲解菱形的性质与判定的综合应用例3解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .(2)若CE=4,∠BCF=120°,求菱形BCFE的面积. 注意:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.新课讲解如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,求平行四边形ABCD的周长.解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,∠BAC=∠ACD.
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠ACD,
∴AD=DC,
∴四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.新课讲解1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形.
(2)对角线互相垂直且平分的四边形是菱形.
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形.
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.√ ╳ ╳ ╳ 2.一边长为5cm的平行四边形的两条对角线的长分别
为24cm和26cm,那么平行四边形的面积是 . 312cm2随堂即练3.如图,矩形ABCD的对角线相交于点O,DE∥AC,
CE ∥BD.求证:四边形OCED是菱形.证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形. 随堂即练4.如图,在平行四边形ABCD中,AC = 6,BD = 8,
AD = 5. 求AB的长.解: ∵ 四边形ABCD为平行四边形,∴ △DAO是直角三角形.∴ ∠DOA = 90°,即DB⊥AC.∴ 平行四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)∴ AB=AD=5 .随堂即练证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,
∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,
∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形. 5.如图,△ABC中,AC的垂直平分线MN交AB于点
D,交AC于点O,CE∥AB交MN于点E,连结AE、
CD.求证:四边形ADCE是菱形.BCN随堂即练四条边都相等菱形一组邻边相等对角线互相垂直对角线互相平分一组对边平行且相等两组对边分别平行或相等四边形平行四边形两组对角分别相等课堂总结
