华东师大版2019年春八年级数学下册19.2.2菱形的判定第1课时菱形的判定定理1课件(17张PPT)
文档属性
| 名称 | 华东师大版2019年春八年级数学下册19.2.2菱形的判定第1课时菱形的判定定理1课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 619.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 00:00:00 | ||
图片预览



文档简介
课件17张PPT。HS八(下)
教学课件第19章 矩形、菱形与主动性18.1 菱形2 菱形的判定第1课时 菱形的判定定理11.运用菱形的定义来判定菱形.(重点)
2.利用菱形的判定定理1来判定菱形.(难点)一组邻边相等有一组邻边相等的平行四边形叫做菱形菱形的性质菱形两组对边平行四条边相等两组对角分别相等 邻角互补两条对角线互相垂直平分
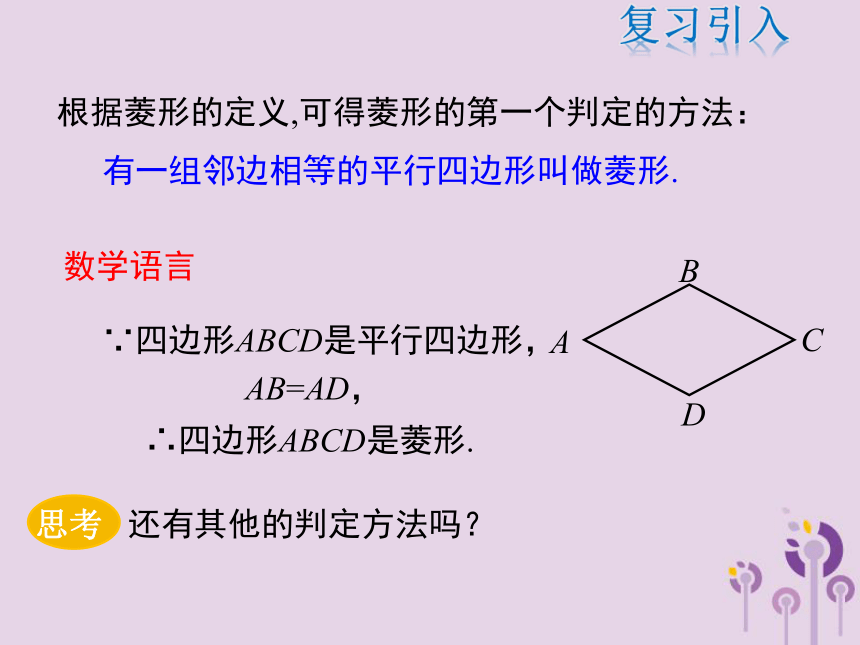
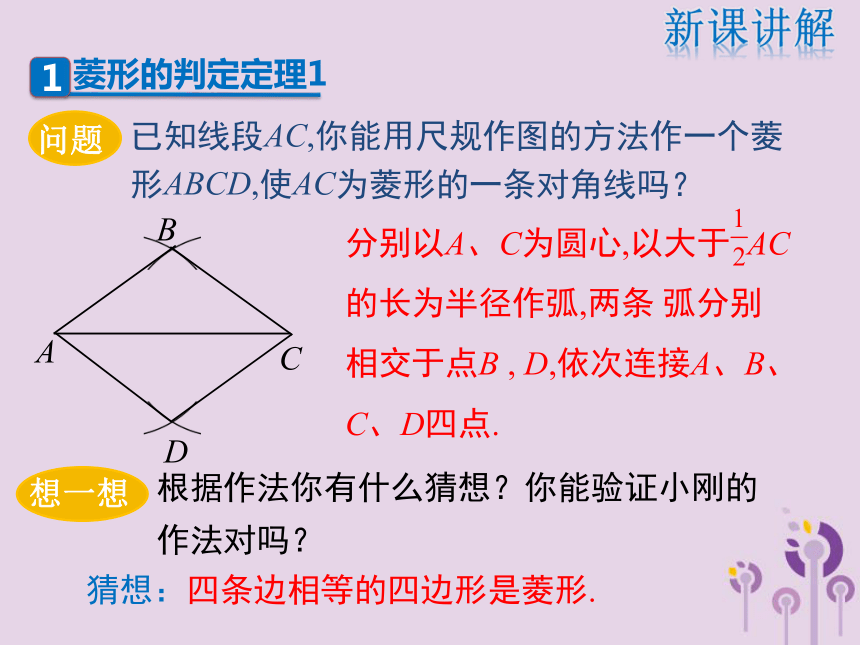
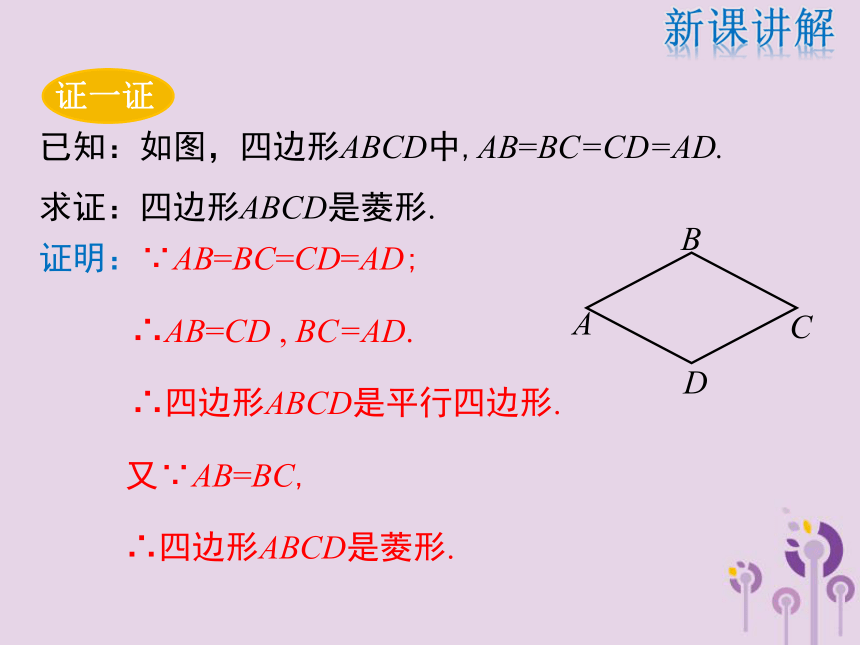
每一条对角线平分一组对角边角对角线复习引入根据菱形的定义,可得菱形的第一个判定的方法:AB=AD,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.数学语言有一组邻边相等的平行四边形叫做菱形.复习引入分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?CABD猜想:四条边相等的四边形是菱形.新课讲解菱形的判定定理1证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.已知:如图,四边形ABCD中,AB=BC=CD=AD.
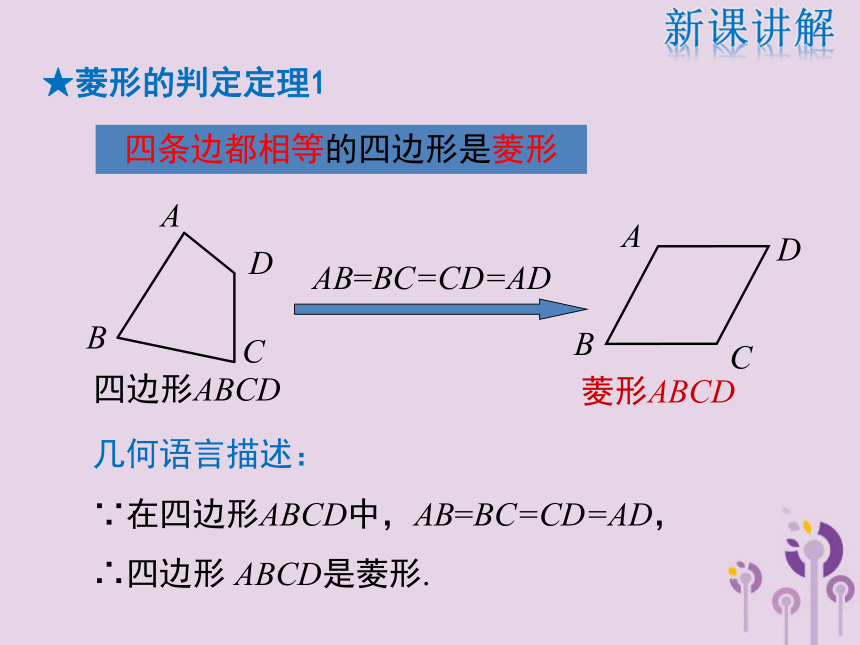
求证:四边形ABCD是菱形.新课讲解四条边都相等的四边形是菱形AB=BC=CD=AD几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,∴四边形 ABCD是菱形.新课讲解★菱形的判定定理1下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C新课讲解证明: ∵ ∠1= ∠2.
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形CDEF是菱形.2 如图,在△ABC中, AD是角平分线,点E、F分别在
AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形. ACBEDF1新课讲解例1证明:∵四边形ABCD是矩形,∴AB=CD,∠A=∠D=90°.∵点F、E、H为AB、AD、CD
的中点,∴△AEF≌△DEH,∴EF=EH,同理可得EF=EH=HG=FG. 如图,顺次连结矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.∴四边形EFGH是菱形.新课讲解例21.如图,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60° B解析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ACED为平行四边形.
当AC=BC时,AC=CE,
平行四边形ACED是菱形.
故选B.随堂即练2.如图,四边形ABCD是平行四边形,延长BA到点E,
使AE=AB,连结ED、EC、AC.添加一个条件,能
使四边形ACDE成为菱形的是( )
A.AB=AD B.AB=ED
C.CD=AE D.EC=ADB随堂即练3.如图,在△ABC中,AD是∠BAC的平分线,EF垂直
平分AD交AB于点E,交AC于点F.
求证:四边形AEDF是菱形.证明:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∵EF⊥AD,∴∠AOE=∠AOF=90°.
在△AEO和△AFO中
∠EAO=∠FAO,AO=AO,∠AOE=∠AOF,
∴△AEO≌△AFO(ASA),
∴EO=FO,AE=AF.
∵EF垂直平分AD,∴EF、AD相互平分,
∴四边形AEDF是平行四边形.
又∵AE=AF,∴平行四边形AEDF为菱形.随堂即练证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.4.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线交BC于点E,连结EF.
(1)求证:四边形ABEF为菱形;随堂即练(2)AE、BF相交于点O,若BF=6,AB=5,求AE的长.解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.随堂即练定义:有一组邻边相等的平行四边形叫
做菱形判定定理1:四边都相等的四边形是菱形菱形的判定课堂总结
教学课件第19章 矩形、菱形与主动性18.1 菱形2 菱形的判定第1课时 菱形的判定定理11.运用菱形的定义来判定菱形.(重点)
2.利用菱形的判定定理1来判定菱形.(难点)一组邻边相等有一组邻边相等的平行四边形叫做菱形菱形的性质菱形两组对边平行四条边相等两组对角分别相等 邻角互补两条对角线互相垂直平分
每一条对角线平分一组对角边角对角线复习引入根据菱形的定义,可得菱形的第一个判定的方法:AB=AD,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.数学语言有一组邻边相等的平行四边形叫做菱形.复习引入分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?CABD猜想:四条边相等的四边形是菱形.新课讲解菱形的判定定理1证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.新课讲解四条边都相等的四边形是菱形AB=BC=CD=AD几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,∴四边形 ABCD是菱形.新课讲解★菱形的判定定理1下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C新课讲解证明: ∵ ∠1= ∠2.
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形CDEF是菱形.2 如图,在△ABC中, AD是角平分线,点E、F分别在
AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形. ACBEDF1新课讲解例1证明:∵四边形ABCD是矩形,∴AB=CD,∠A=∠D=90°.∵点F、E、H为AB、AD、CD
的中点,∴△AEF≌△DEH,∴EF=EH,同理可得EF=EH=HG=FG. 如图,顺次连结矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.∴四边形EFGH是菱形.新课讲解例21.如图,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60° B解析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ACED为平行四边形.
当AC=BC时,AC=CE,
平行四边形ACED是菱形.
故选B.随堂即练2.如图,四边形ABCD是平行四边形,延长BA到点E,
使AE=AB,连结ED、EC、AC.添加一个条件,能
使四边形ACDE成为菱形的是( )
A.AB=AD B.AB=ED
C.CD=AE D.EC=ADB随堂即练3.如图,在△ABC中,AD是∠BAC的平分线,EF垂直
平分AD交AB于点E,交AC于点F.
求证:四边形AEDF是菱形.证明:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∵EF⊥AD,∴∠AOE=∠AOF=90°.
在△AEO和△AFO中
∠EAO=∠FAO,AO=AO,∠AOE=∠AOF,
∴△AEO≌△AFO(ASA),
∴EO=FO,AE=AF.
∵EF垂直平分AD,∴EF、AD相互平分,
∴四边形AEDF是平行四边形.
又∵AE=AF,∴平行四边形AEDF为菱形.随堂即练证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.4.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线交BC于点E,连结EF.
(1)求证:四边形ABEF为菱形;随堂即练(2)AE、BF相交于点O,若BF=6,AB=5,求AE的长.解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.随堂即练定义:有一组邻边相等的平行四边形叫
做菱形判定定理1:四边都相等的四边形是菱形菱形的判定课堂总结
