青岛版九年级数学上册1.1 相似多边形课件(21张PPT)
文档属性
| 名称 | 青岛版九年级数学上册1.1 相似多边形课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-24 00:00:00 | ||
图片预览







文档简介
1.1 相似多边形
第一章
1.从生活中形状相同的图形的实例中认识
图形的相似,理解相似图形的概念;
2.理解相似图形的性质和判定.
学习目标
请观察下面几组图片你能发现它们有什么特点吗?
形状相同,大小不一定相同
形状相同的平面图形叫做相似形.
两两相似的几何图形
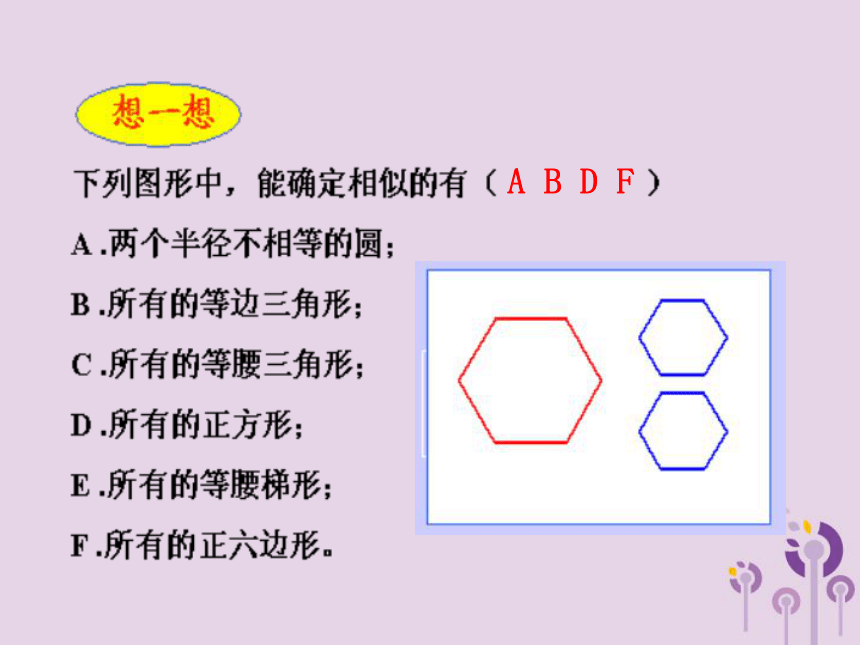
A B D F
下列图形中____与_____是相似的.
(1) (2) (3) (4)
选一选
(1) (4)
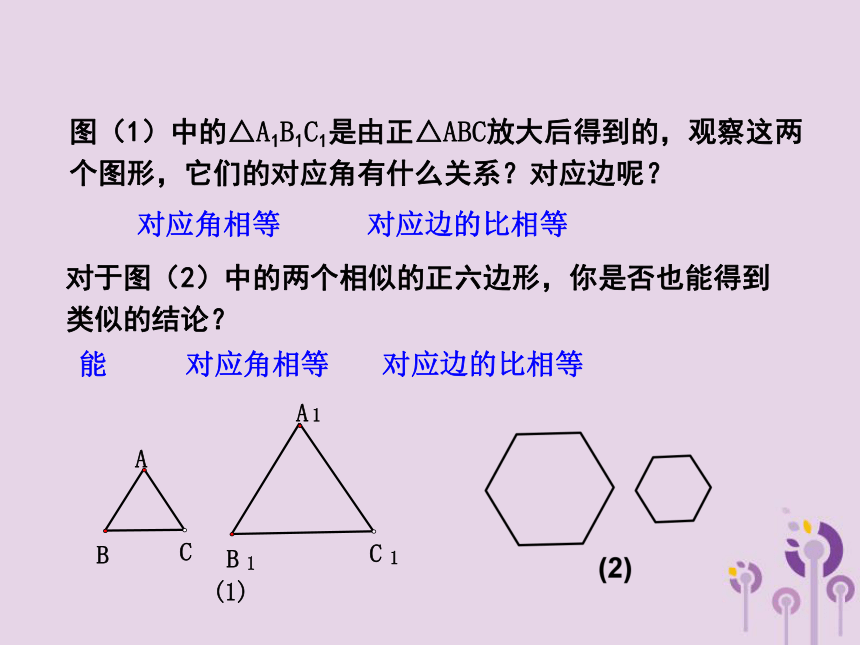
图(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对于图(2)中的两个相似的正六边形,你是否也能得到类似的结论?
对应角相等
对应边的比相等
对应角相等
对应边的比相等
能
A
(1)
C
1
B
1
1
C
B
A
图(1)是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
对于图(2)中两个相似的四边形,它们的对应角、对应边是否有同样的结论?
对应角相等
对应边的比相等
有
对应角相等
对应边的比相等
(1)
(2)
相似多边形各个角对应相等,各边对应成比例.
相似多边形的定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等,各边对应成比例,那么这两个多边形叫做相似多边形.
相似多边形的性质:
符号“∽”读作“相似于”
对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段.
相似多边形对应边的比叫做相似比
全等
相似比为1时,相似的两个图形有什么关系?
【例1】 如图,四边形AEFD∽EBCF.
(1)写出它们相等的角即对应边的比例式;
(2)若AD=3,EF=4,求BC 的长.
A D
E F
B C
解(1)在四边形AEFD和四边形EBCF中,
∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,∠DFE=∠C,∠D=∠EFC.
并且
如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
【解析】四边形ABCD和EFGH 相似,它们的对应角相等.
由此可得
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
四边形ABCD 和EFGH 相似,它们的对应边的比相等.
由此可得
解得 x=28cm.
1.下列各组线段(单位:㎝)中,成比例线段的是( )
A.1、2、3、4 B.1、2、2、4
C.3、5、9、13 D.1、2、2、3
B
【课堂练习】
2.下列说法中,错误的是( )
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正方形都相似
3. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边框,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )
C
D
4.在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离.
设两地的实际距离为xcm
x = 300 000 000(cm),
x=3000 km
答:甲、乙两地的实际距离为3000 km.
【解析】
1 30
10 000 000 x
=
5. 如图所示的两个五边形相似,求未知边a,b,c,d的长度.
5
3
2
c
d
7.5
b
a
6
9
【解析】由图所示, 可知两图形的相似比为:
b = 4.5
a = 3
c = 4
d = 6
1.理解相似图形的性质
2.完成习题1.1的相关习题
第一章
1.从生活中形状相同的图形的实例中认识
图形的相似,理解相似图形的概念;
2.理解相似图形的性质和判定.
学习目标
请观察下面几组图片你能发现它们有什么特点吗?
形状相同,大小不一定相同
形状相同的平面图形叫做相似形.
两两相似的几何图形
A B D F
下列图形中____与_____是相似的.
(1) (2) (3) (4)
选一选
(1) (4)
图(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对于图(2)中的两个相似的正六边形,你是否也能得到类似的结论?
对应角相等
对应边的比相等
对应角相等
对应边的比相等
能
A
(1)
C
1
B
1
1
C
B
A
图(1)是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
对于图(2)中两个相似的四边形,它们的对应角、对应边是否有同样的结论?
对应角相等
对应边的比相等
有
对应角相等
对应边的比相等
(1)
(2)
相似多边形各个角对应相等,各边对应成比例.
相似多边形的定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等,各边对应成比例,那么这两个多边形叫做相似多边形.
相似多边形的性质:
符号“∽”读作“相似于”
对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段.
相似多边形对应边的比叫做相似比
全等
相似比为1时,相似的两个图形有什么关系?
【例1】 如图,四边形AEFD∽EBCF.
(1)写出它们相等的角即对应边的比例式;
(2)若AD=3,EF=4,求BC 的长.
A D
E F
B C
解(1)在四边形AEFD和四边形EBCF中,
∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,∠DFE=∠C,∠D=∠EFC.
并且
如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
【解析】四边形ABCD和EFGH 相似,它们的对应角相等.
由此可得
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
四边形ABCD 和EFGH 相似,它们的对应边的比相等.
由此可得
解得 x=28cm.
1.下列各组线段(单位:㎝)中,成比例线段的是( )
A.1、2、3、4 B.1、2、2、4
C.3、5、9、13 D.1、2、2、3
B
【课堂练习】
2.下列说法中,错误的是( )
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正方形都相似
3. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边框,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )
C
D
4.在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离.
设两地的实际距离为xcm
x = 300 000 000(cm),
x=3000 km
答:甲、乙两地的实际距离为3000 km.
【解析】
1 30
10 000 000 x
=
5. 如图所示的两个五边形相似,求未知边a,b,c,d的长度.
5
3
2
c
d
7.5
b
a
6
9
【解析】由图所示, 可知两图形的相似比为:
b = 4.5
a = 3
c = 4
d = 6
1.理解相似图形的性质
2.完成习题1.1的相关习题
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
