苏科版七年级数学下册9.4 乘法公式课件(共21张PPT)
文档属性
| 名称 | 苏科版七年级数学下册9.4 乘法公式课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 848.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 14:07:37 | ||
图片预览





文档简介
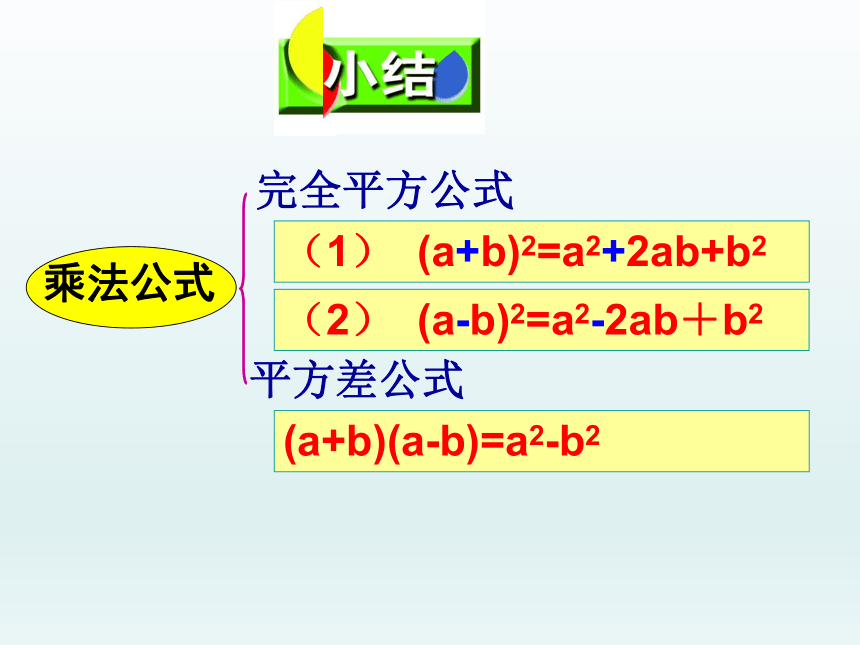
课件21张PPT。§9.4 乘法公式 上节课我们学习的知识是什么?知识回顾完全平方公式(1) (a+b)2=a2+2ab+b2(2) (a-b)2=a2-2ab+b2用完全平方公式计算: (2a-3)2
(-x+4y)2
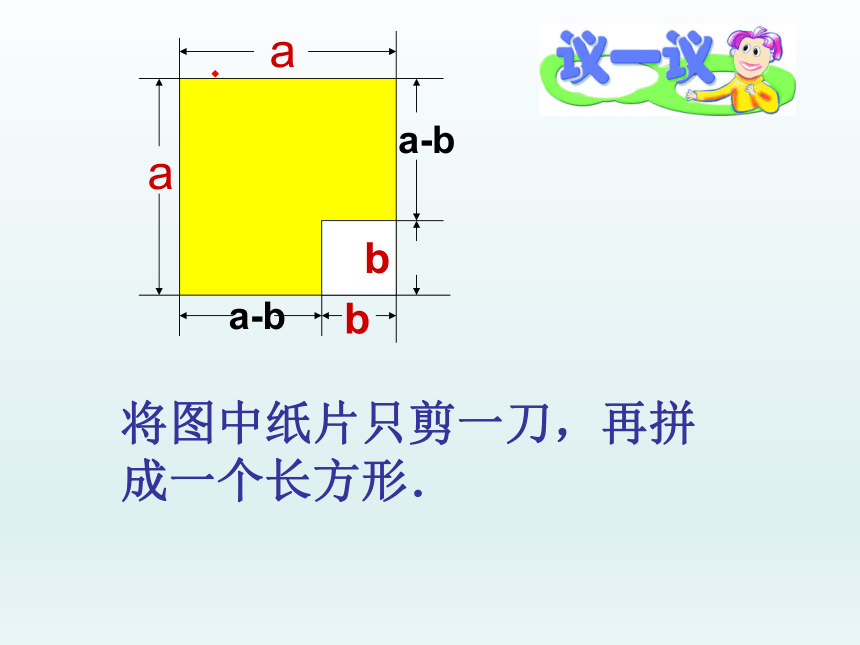
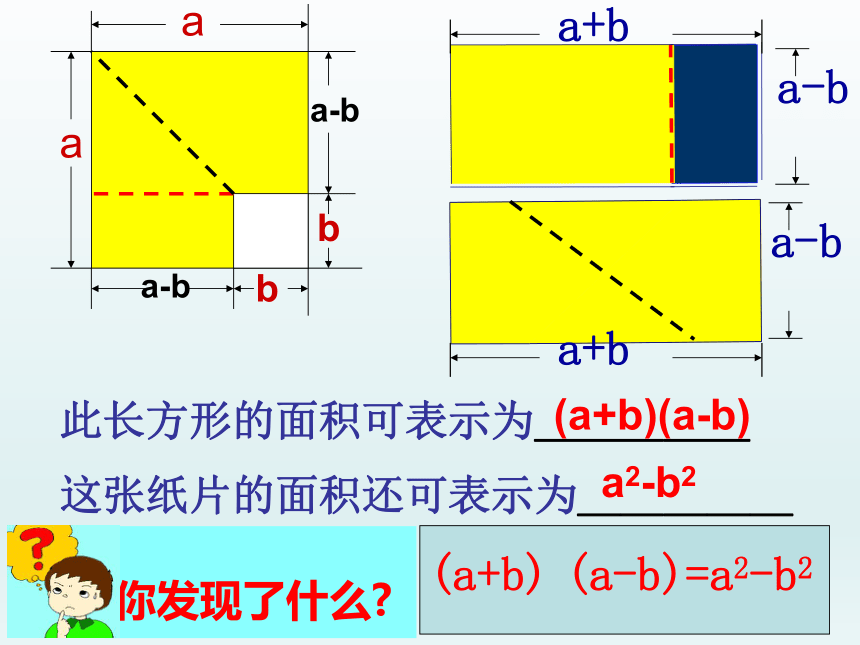
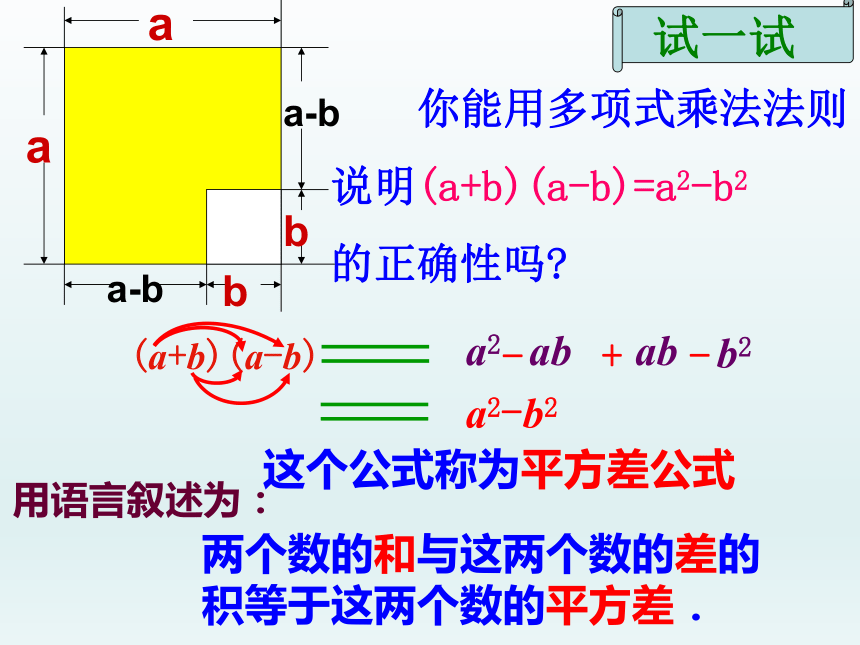
(3) 1022将图中纸片只剪一刀,再拼成一个长方形.aabba-ba-baabba-ba-b此长方形的面积可表示为_____这张纸片的面积还可表示为_____(a+b)(a-b)a2-b2(a+b) (a-b)=a2-b2aabba-ba-b两个数的和与这两个数的差的积等于这两个数的平方差.用语言叙述为:这个公式称为平方差公式 你能用多项式乘法法则
说明(a+b)(a-b)=a2-b2
的正确性吗?(a+b)(a-b)a2a2-b2语言叙述:两数和与它们差的积等于这两个数的平方差.平方差公式特点:
公式的左边:
两个二项式的积,其中有一项(a)完全相同,另一项(b和-b)互为相反数;
公式的右边:
这两项的平方差。
说说平方差公式的特点.前一个数的平方后一个数的平方完全平方公式(1) (a+b)2=a2+2ab+b2(2) (a-b)2=a2-2ab+b2平方差公式(a+b)(a-b)=a2-b2平方差公式:我知道啦(a+b)(a-b)=a2-b2例1.用平方差公式计算:(1) (x+2y)(x-2y)
(2) (3+2x)(2x-3)
(3) (3a-b)(-b-3a)注意:①公式中的a与b可以是数也可以是单项式、多项式或其他代数式。
②正确判断哪个数为a,哪个数为b
(与位置、自身的性质符号无关,两因式中的两对数是否有一个数完全相同,而另一个数是相反数)。1.选择:下列各式中,能用平方差公式的是 ( )
A.(x-3)(-x+3) B.(x+2y)(2x-y)
C.(y-1)(-y-1) D.(y+1)(-y-1)C3.判断:(1)(x+3)(x-2)=x2-6 ( )(2)(y+2)(x-2)=xy-4 ( )(3)(2y+3)(-2y+3)=9-4y2 ( )(4)(3-2y)2=9-4y2 ( ) ×√××4.填空:(1)(2x-__)(__+3y)=____-9y2
(2)(______)(-4x-3y)=16x2-9y23y2x4x2- 4x+3y例2.用简便方法计算:
(1) 101×99
(2)练习:用简便方法计算:
(1)22×18 (2)例3 填空: 665n5nb-a5 25随堂演练小结公式的结构特征:左边是a2 ? b2 两个二项式的乘积,平方差公式 对于一般两个二项式的积, 看准有无相等的“项”和符号相反的“项”; 仅当把两个二项式的积变成公式标准形式后,才能使用平方差公式。 (a+b)(a?b)=即两数和与这两数差的积.右边是两数的平方差.1.下列计算是否正确? (1)(2)如有错误,请改正.2.用完全平方公式计算(1)(2)(3)(4)3.用乘法公式计算
49×51
(2) (a+2)(a-2)-(a-1)(a+5)(4) (-3x-2y)(3x-2y)
(3x-1)(3x+1) -(2x+3)(2x-3)
(6) (2x+y)( -y+2x)-(2x-y)2
(-x+4y)2
(3) 1022将图中纸片只剪一刀,再拼成一个长方形.aabba-ba-baabba-ba-b此长方形的面积可表示为_____这张纸片的面积还可表示为_____(a+b)(a-b)a2-b2(a+b) (a-b)=a2-b2aabba-ba-b两个数的和与这两个数的差的积等于这两个数的平方差.用语言叙述为:这个公式称为平方差公式 你能用多项式乘法法则
说明(a+b)(a-b)=a2-b2
的正确性吗?(a+b)(a-b)a2a2-b2语言叙述:两数和与它们差的积等于这两个数的平方差.平方差公式特点:
公式的左边:
两个二项式的积,其中有一项(a)完全相同,另一项(b和-b)互为相反数;
公式的右边:
这两项的平方差。
说说平方差公式的特点.前一个数的平方后一个数的平方完全平方公式(1) (a+b)2=a2+2ab+b2(2) (a-b)2=a2-2ab+b2平方差公式(a+b)(a-b)=a2-b2平方差公式:我知道啦(a+b)(a-b)=a2-b2例1.用平方差公式计算:(1) (x+2y)(x-2y)
(2) (3+2x)(2x-3)
(3) (3a-b)(-b-3a)注意:①公式中的a与b可以是数也可以是单项式、多项式或其他代数式。
②正确判断哪个数为a,哪个数为b
(与位置、自身的性质符号无关,两因式中的两对数是否有一个数完全相同,而另一个数是相反数)。1.选择:下列各式中,能用平方差公式的是 ( )
A.(x-3)(-x+3) B.(x+2y)(2x-y)
C.(y-1)(-y-1) D.(y+1)(-y-1)C3.判断:(1)(x+3)(x-2)=x2-6 ( )(2)(y+2)(x-2)=xy-4 ( )(3)(2y+3)(-2y+3)=9-4y2 ( )(4)(3-2y)2=9-4y2 ( ) ×√××4.填空:(1)(2x-__)(__+3y)=____-9y2
(2)(______)(-4x-3y)=16x2-9y23y2x4x2- 4x+3y例2.用简便方法计算:
(1) 101×99
(2)练习:用简便方法计算:
(1)22×18 (2)例3 填空: 665n5nb-a5 25随堂演练小结公式的结构特征:左边是a2 ? b2 两个二项式的乘积,平方差公式 对于一般两个二项式的积, 看准有无相等的“项”和符号相反的“项”; 仅当把两个二项式的积变成公式标准形式后,才能使用平方差公式。 (a+b)(a?b)=即两数和与这两数差的积.右边是两数的平方差.1.下列计算是否正确? (1)(2)如有错误,请改正.2.用完全平方公式计算(1)(2)(3)(4)3.用乘法公式计算
49×51
(2) (a+2)(a-2)-(a-1)(a+5)(4) (-3x-2y)(3x-2y)
(3x-1)(3x+1) -(2x+3)(2x-3)
(6) (2x+y)( -y+2x)-(2x-y)2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
