苏科版七年级数学下册9.1 单项式乘单项式课件(共29张PPT)
文档属性
| 名称 | 苏科版七年级数学下册9.1 单项式乘单项式课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 398.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 14:05:05 | ||
图片预览








文档简介
课件29张PPT。1下列整式中哪些是单项式?哪些是多项式?知识复习:2、利用乘法的交换律,结合律计算:
6×4×13×25解:原式= (6 ×13) ×(4×25) =78 ×100=7800知识复习:3、前面学习了哪三种幂的运算?
运算方法分别是什么?
公式的逆运算你会吗?知识复习:1、同底数幂相乘,底数不变,指数相加。一般形式: 2、幂的乘方,底数不变,指数相乘一般形式:( n ,m 为正整数)(m,n为正整数)3、 积的乘方等于各因数乘方的积
一般形式:(n为正整数)
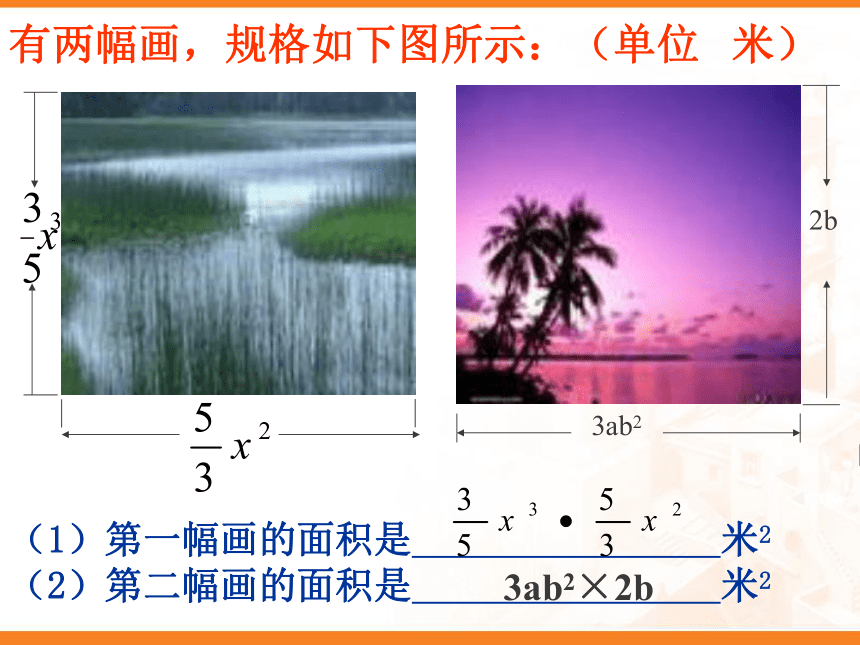
知识复习:有两幅画,规格如下图所示:(单位 米)(1)第一幅画的面积是 米2
(2)第二幅画的面积是 米2 3ab2×2b乘法交换律(ab=ba)
乘法结合律(ab)c=a(bc) 5×1031.2×102( ) ( )× = ( 5× ) ×( ×102) =6×1051.2103 变式1: 5___·1.2___a4a3=(___×____)(___·____)=____ 5a4a3 6a7变式2: 5a4·(-1.2a3b2)=[__×(-1.2)] ●(a4a3)__ 5b2=-6a7b2合作探究:1.2从以上这些式子中你能发现进行单项式与单项式相乘的运算规律吗?1、系数相乘2、同底数的幂相乘3、只在一个单项式里含有的字母,
连同它的指数作为积的一个因式。有理数的乘法单项式的乘法法则包括以下三部分:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.
(注意 不要把这个因式丢掉)
(同底数幂的乘法) 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.单项式的乘法法则 同 学 们,你 们 知 道 我 们 的教 室 有 多 大 吗? 小 明 想 要 估 算 它 的 面 积,你 能 帮 助 他 解 决 问 题 吗?考考你 小明采用步长测量教室的面积,测量长时走了13步,测量宽时走了9步,如果小明的步长用a米表示, 你能用含a的代数式表示教室的面积吗?若小明的步长为0.7米,那么教室面积约是多少?解:(13a) ? (9a)(13× 0.7) ? (9 × 0.7)= 9.1 × 6.3=57.33(m2)(根据什么?)(乘法交换律和结合律)=(13 ×9 )×(a ? a)=117a2=57.33 (m2)例题2:卫星绕地球运动的速度(即第一宇宙速度)约为7.9× 米/秒,则卫星运行3× 秒所走的路程约是多少米?解: 7.9× × 3×=23.7 ×=2.37 ×答:卫星绕地球运行3× 秒走过的路程约是2.37 × 米。结果要用科学记数法表示研究课题:下面的三个式子可以表达的更简单吗?你的理由是什么? 分组研究!(1)(2)(3)解:原式各因数系数结合成一组相同的字母结合成一组系数的积作为积的系数对于相同的字母,用它们的指数和作为积里这个字母的指数对于只有一个单项式里含有的字母,连同它的指数作为积的一个因式(3)探究尝试(系数×系数)(同底数幂相乘)×单独的幂计算:解:原式=单项式与单项式相乘的法则 单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。例1:计算解:原式解:原式解:原式例3 计算
(-2a2)3 ·(-3a3)2
观察一下,例3比例2多了什么运算?例2 计算
例3 计算:
(1)(2?104)(5 ? 103) ? 107解(1)原式=(2 ?5)(104 ×103× 107 )=10?1014=1015(2) (4 ? 105) ·(5 ? 106) ·(3?104)(2)原式=(4?5 ? 3)(105 ? 106 ? 104)=60?1015=6?1016这里有三个单项式
相乘,还可以利用
上面的法则吗?计算:解:原式
单项式与单项式相乘的运算法则B××××判断正误:(1)4a2 ?2a4 = 8a8 ( ) (2)6a3 ?5a2=11a5 ( ) (3)(-7a)?(-3a3) =-21a4 ( ) (4)3a2b ?4a3=12a5 ( ) 系数相乘同底数幂的乘法,底数不变,指数相加只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号求系数的积,应注意符号;相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;单项式乘法的法则对于三个以上的单项式相乘同样适用。提 示: (2)2细心填一填:
(1) ( )3计算: 1、2、3x2y ? (-2xy3);
(-5a2b3)? (-4b2c) 解:(1)3x2y ? (-2xy3)
= [3 ? (-2)] ? (x2 ? x)? (y ? y3)
= -6x3y4 (2)(-5a2b3)? (-4b2c)
=[(-5)? (-4)] ? a2? (b3 ? b2)? c
=20a2b5c2.计算:(1)(-2x2)·(-3x2y3)2=________;-18x6y6(2)(-2xy2)2·(-3xyn)·(-x2z)=________.12x5y4+nz(1)原式= (-2x2)·(9 x4y6)(2)原式=(4x2y4) ·(-3xyn)·(-x2z)-9x3y2a2bXn+2a6nb6n2?1012计算:提高题:计算: 请 你 算 一 算: 单项式与单项式相乘同底数幂相乘只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式系数乘以系数
6×4×13×25解:原式= (6 ×13) ×(4×25) =78 ×100=7800知识复习:3、前面学习了哪三种幂的运算?
运算方法分别是什么?
公式的逆运算你会吗?知识复习:1、同底数幂相乘,底数不变,指数相加。一般形式: 2、幂的乘方,底数不变,指数相乘一般形式:( n ,m 为正整数)(m,n为正整数)3、 积的乘方等于各因数乘方的积
一般形式:(n为正整数)
知识复习:有两幅画,规格如下图所示:(单位 米)(1)第一幅画的面积是 米2
(2)第二幅画的面积是 米2 3ab2×2b乘法交换律(ab=ba)
乘法结合律(ab)c=a(bc) 5×1031.2×102( ) ( )× = ( 5× ) ×( ×102) =6×1051.2103 变式1: 5___·1.2___a4a3=(___×____)(___·____)=____ 5a4a3 6a7变式2: 5a4·(-1.2a3b2)=[__×(-1.2)] ●(a4a3)__ 5b2=-6a7b2合作探究:1.2从以上这些式子中你能发现进行单项式与单项式相乘的运算规律吗?1、系数相乘2、同底数的幂相乘3、只在一个单项式里含有的字母,
连同它的指数作为积的一个因式。有理数的乘法单项式的乘法法则包括以下三部分:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.
(注意 不要把这个因式丢掉)
(同底数幂的乘法) 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.单项式的乘法法则 同 学 们,你 们 知 道 我 们 的教 室 有 多 大 吗? 小 明 想 要 估 算 它 的 面 积,你 能 帮 助 他 解 决 问 题 吗?考考你 小明采用步长测量教室的面积,测量长时走了13步,测量宽时走了9步,如果小明的步长用a米表示, 你能用含a的代数式表示教室的面积吗?若小明的步长为0.7米,那么教室面积约是多少?解:(13a) ? (9a)(13× 0.7) ? (9 × 0.7)= 9.1 × 6.3=57.33(m2)(根据什么?)(乘法交换律和结合律)=(13 ×9 )×(a ? a)=117a2=57.33 (m2)例题2:卫星绕地球运动的速度(即第一宇宙速度)约为7.9× 米/秒,则卫星运行3× 秒所走的路程约是多少米?解: 7.9× × 3×=23.7 ×=2.37 ×答:卫星绕地球运行3× 秒走过的路程约是2.37 × 米。结果要用科学记数法表示研究课题:下面的三个式子可以表达的更简单吗?你的理由是什么? 分组研究!(1)(2)(3)解:原式各因数系数结合成一组相同的字母结合成一组系数的积作为积的系数对于相同的字母,用它们的指数和作为积里这个字母的指数对于只有一个单项式里含有的字母,连同它的指数作为积的一个因式(3)探究尝试(系数×系数)(同底数幂相乘)×单独的幂计算:解:原式=单项式与单项式相乘的法则 单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。例1:计算解:原式解:原式解:原式例3 计算
(-2a2)3 ·(-3a3)2
观察一下,例3比例2多了什么运算?例2 计算
例3 计算:
(1)(2?104)(5 ? 103) ? 107解(1)原式=(2 ?5)(104 ×103× 107 )=10?1014=1015(2) (4 ? 105) ·(5 ? 106) ·(3?104)(2)原式=(4?5 ? 3)(105 ? 106 ? 104)=60?1015=6?1016这里有三个单项式
相乘,还可以利用
上面的法则吗?计算:解:原式
单项式与单项式相乘的运算法则B××××判断正误:(1)4a2 ?2a4 = 8a8 ( ) (2)6a3 ?5a2=11a5 ( ) (3)(-7a)?(-3a3) =-21a4 ( ) (4)3a2b ?4a3=12a5 ( ) 系数相乘同底数幂的乘法,底数不变,指数相加只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号求系数的积,应注意符号;相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;单项式乘法的法则对于三个以上的单项式相乘同样适用。提 示: (2)2细心填一填:
(1) ( )3计算: 1、2、3x2y ? (-2xy3);
(-5a2b3)? (-4b2c) 解:(1)3x2y ? (-2xy3)
= [3 ? (-2)] ? (x2 ? x)? (y ? y3)
= -6x3y4 (2)(-5a2b3)? (-4b2c)
=[(-5)? (-4)] ? a2? (b3 ? b2)? c
=20a2b5c2.计算:(1)(-2x2)·(-3x2y3)2=________;-18x6y6(2)(-2xy2)2·(-3xyn)·(-x2z)=________.12x5y4+nz(1)原式= (-2x2)·(9 x4y6)(2)原式=(4x2y4) ·(-3xyn)·(-x2z)-9x3y2a2bXn+2a6nb6n2?1012计算:提高题:计算: 请 你 算 一 算: 单项式与单项式相乘同底数幂相乘只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式系数乘以系数
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
