北师大版数学七年级下册 2.3 平行线的性质 (1)课件(共19张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 2.3 平行线的性质 (1)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 15:34:07 | ||
图片预览





文档简介
第三节 平行线的特征
北师大版起年级数学下册
第二章 相交线与平行线
(1)∵ ∠1__∠2 (已知)
∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b (? )
=
同位角相等,两直线平行
=
内错角相等,两直线平行
180°
同旁内角互补,两直线平行
(3)∵ ∠2+∠4=____(已知),
∴ a ∥ b ( ??? )
回忆再现
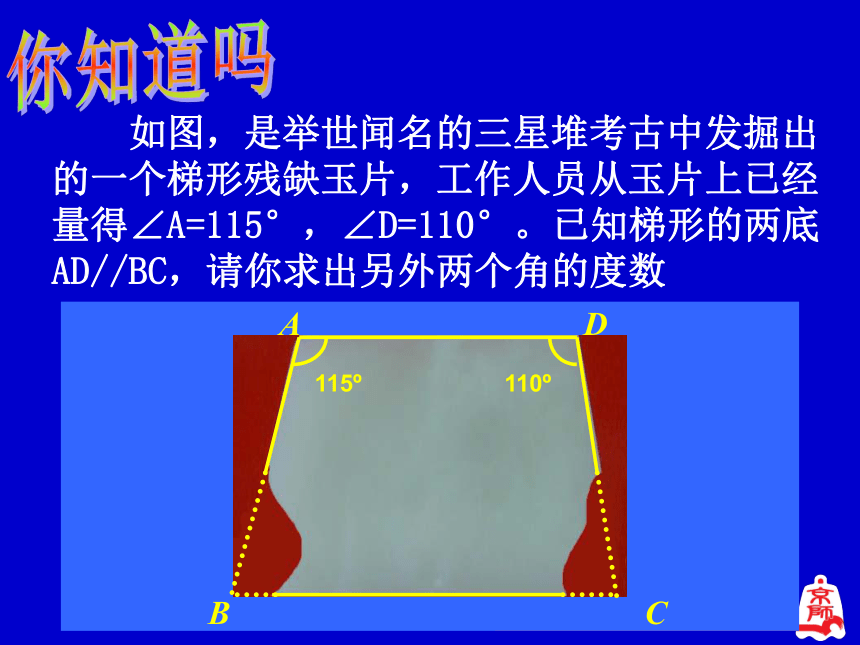
你知道吗
三星堆遗址位于中国四川省广汉市南兴镇,属于古蜀国文明。遗址分布范围达12平方公里,距今4800年至2800年,延续时间近2000年。
出土了各种文物:金器、玉器、石器、陶器、青铜器...等数千件。其中有享誉中外的金杖、金面罩、青铜人像、头像、人立像、画具等精品文物1000多件。
三星堆遗址
你知道吗
A
D
C
115?
110?
B
如图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数
交流合作,探索发现
请同学们任意画出两条平行线a,b,并作一条与两条平行线都相交的直线c,
合作交流一:
请找出图中的同位角,并猜测他们有何关系?你能想办法验证你的猜测吗?
a
b
c
1
7
4
5
6
3
2
8
两直线平行,同位角相等
猜想1
平行线的特征1
交流合作,探索发现
合作交流二:
图中还有几组内错角,猜测一下它们又有何关系呢?你能想办法验证你的猜测吗?
a
b
c
1
7
4
5
6
3
2
8
两直线平行,内错角相等
猜想2
平行线的特征2
交流合作,探索发现
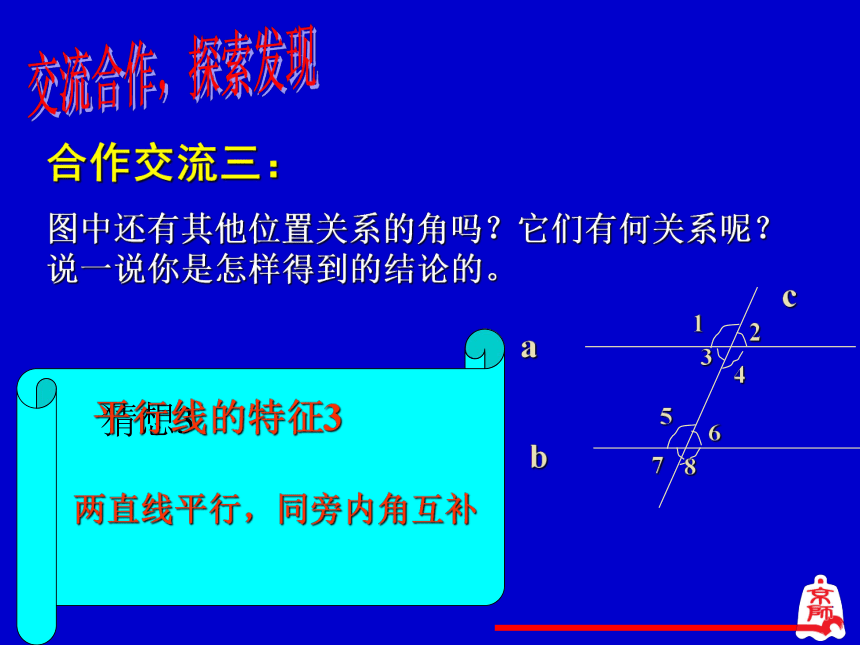
合作交流三:
图中还有其他位置关系的角吗?它们有何关系呢?说一说你是怎样得到的结论的。
a
b
c
1
7
4
5
6
3
2
8
猜想3
两直线平行,同旁内角互补
平行线的特征3
简记为
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
平行线的特征
规律
两条平行直线被第三条直线所截,
同位角相等,内错角相等,同旁内角互补。
重 点
牛刀小试
1. ∵ AD//BC (已知)
∴ ∠B=∠1 ( )
2. ∵ AB//CD (已知)
∴ ∠D=∠1 ( )
3. ∵ AD//BC (已知)
∴ ∠C+_______=180?( )
A
B
C
D
1
两直线平行,同位角相等
两直线平行,内错角相等
∠D
两直线平行,同旁内角互补
如图所示,AB∥CD,AC ∥BD, 分别找出与∠1相等或互补的角.
A
D
C
B
1
6
5
4
3
2
7
8
14
13
15
16
10
9
11
12
如图,与∠1相等的角有:
∠3, ∠5, ∠7, ∠9,
∠11, ∠13, ∠15;
与∠1互补的角有:
∠2, ∠4, ∠6, ∠8,
∠10, ∠12, ∠14, ∠16 .
解:
牛刀小试
现在你知道了吗
A
D
C
115?
110?
B
工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
∴∠A+∠B=180o
∠C=180o-110o=70o
∴梯形的另外两个角分别是65o和70o。
∠D+∠C=180o
∵ ∠A=115°,∠D=110°(已知)
(等式的性质)
解:∵AD∥BC(已知)
∴∠B=180o-115o=65o
(两直线平行,同旁内角互补)
著名的比萨斜塔建成于12世纪,从建成之日起就一直在倾斜,目前,它与地面所成的较小的角为85?(如图),它与地面所成的较大的角是多少度?
85?
?
95
0
建筑趣闻
平行线的特征
直线平行的条件
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
填写下列表格,并思考二者有何区别和练习:
两直线平行
同位角相等
内错角相等
同旁内角互补
特征
条件
对比发现,加深理解
B
E
1
2
3
4
C
F
D
A
B
E
如图所示,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3= ∠4。
(1)∠1 ,∠3的大小有什么关系? ∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
链接生活
小红是这样想的,你能明白她的意思吗?每一步的根据是什么?
(1) AB // DE
∠1 =∠3
∠1 =∠3
∠1 =∠2
∠3 =∠4
∠2=∠4
(2)
∠2=∠4
BC // EF
和同学交流一下,谈谈你的看法
拓展巩固
潜望镜中的两面镜子是平行放置的,如图所示,光线经镜子反射后, ∠1=∠2,∠3= ∠4。你能从数学的角度解释一下进入潜望镜的光线和离开潜望镜的光线为什么是平行的吗?
1
2
3
4
颗粒归仓
1. 本节课学习了平行线的三个特征
两直线平行
同位角相等
内错角相等
同旁内角互补
2. 直线平行的特征与直线平行的条件的区别。
(1)识别与特征的条件与结论有什么关系?
互换。
(2)使用识别时是已知 ___,说明________
角的相等或互补
两直线平行
使用特征时是已知 ,说明_____________
两直线平行
角的相等或互补
3. 几何中的计算往往要说理,要熟悉几何里计算题的格式,学
习合情说理。
作业
1. 习题2.4 知识技能1,2
2. 习题2.4 问题解决
谢谢合作!
北师大版起年级数学下册
第二章 相交线与平行线
(1)∵ ∠1__∠2 (已知)
∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b (? )
=
同位角相等,两直线平行
=
内错角相等,两直线平行
180°
同旁内角互补,两直线平行
(3)∵ ∠2+∠4=____(已知),
∴ a ∥ b ( ??? )
回忆再现
你知道吗
三星堆遗址位于中国四川省广汉市南兴镇,属于古蜀国文明。遗址分布范围达12平方公里,距今4800年至2800年,延续时间近2000年。
出土了各种文物:金器、玉器、石器、陶器、青铜器...等数千件。其中有享誉中外的金杖、金面罩、青铜人像、头像、人立像、画具等精品文物1000多件。
三星堆遗址
你知道吗
A
D
C
115?
110?
B
如图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数
交流合作,探索发现
请同学们任意画出两条平行线a,b,并作一条与两条平行线都相交的直线c,
合作交流一:
请找出图中的同位角,并猜测他们有何关系?你能想办法验证你的猜测吗?
a
b
c
1
7
4
5
6
3
2
8
两直线平行,同位角相等
猜想1
平行线的特征1
交流合作,探索发现
合作交流二:
图中还有几组内错角,猜测一下它们又有何关系呢?你能想办法验证你的猜测吗?
a
b
c
1
7
4
5
6
3
2
8
两直线平行,内错角相等
猜想2
平行线的特征2
交流合作,探索发现
合作交流三:
图中还有其他位置关系的角吗?它们有何关系呢?说一说你是怎样得到的结论的。
a
b
c
1
7
4
5
6
3
2
8
猜想3
两直线平行,同旁内角互补
平行线的特征3
简记为
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
平行线的特征
规律
两条平行直线被第三条直线所截,
同位角相等,内错角相等,同旁内角互补。
重 点
牛刀小试
1. ∵ AD//BC (已知)
∴ ∠B=∠1 ( )
2. ∵ AB//CD (已知)
∴ ∠D=∠1 ( )
3. ∵ AD//BC (已知)
∴ ∠C+_______=180?( )
A
B
C
D
1
两直线平行,同位角相等
两直线平行,内错角相等
∠D
两直线平行,同旁内角互补
如图所示,AB∥CD,AC ∥BD, 分别找出与∠1相等或互补的角.
A
D
C
B
1
6
5
4
3
2
7
8
14
13
15
16
10
9
11
12
如图,与∠1相等的角有:
∠3, ∠5, ∠7, ∠9,
∠11, ∠13, ∠15;
与∠1互补的角有:
∠2, ∠4, ∠6, ∠8,
∠10, ∠12, ∠14, ∠16 .
解:
牛刀小试
现在你知道了吗
A
D
C
115?
110?
B
工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
∴∠A+∠B=180o
∠C=180o-110o=70o
∴梯形的另外两个角分别是65o和70o。
∠D+∠C=180o
∵ ∠A=115°,∠D=110°(已知)
(等式的性质)
解:∵AD∥BC(已知)
∴∠B=180o-115o=65o
(两直线平行,同旁内角互补)
著名的比萨斜塔建成于12世纪,从建成之日起就一直在倾斜,目前,它与地面所成的较小的角为85?(如图),它与地面所成的较大的角是多少度?
85?
?
95
0
建筑趣闻
平行线的特征
直线平行的条件
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
填写下列表格,并思考二者有何区别和练习:
两直线平行
同位角相等
内错角相等
同旁内角互补
特征
条件
对比发现,加深理解
B
E
1
2
3
4
C
F
D
A
B
E
如图所示,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3= ∠4。
(1)∠1 ,∠3的大小有什么关系? ∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
链接生活
小红是这样想的,你能明白她的意思吗?每一步的根据是什么?
(1) AB // DE
∠1 =∠3
∠1 =∠3
∠1 =∠2
∠3 =∠4
∠2=∠4
(2)
∠2=∠4
BC // EF
和同学交流一下,谈谈你的看法
拓展巩固
潜望镜中的两面镜子是平行放置的,如图所示,光线经镜子反射后, ∠1=∠2,∠3= ∠4。你能从数学的角度解释一下进入潜望镜的光线和离开潜望镜的光线为什么是平行的吗?
1
2
3
4
颗粒归仓
1. 本节课学习了平行线的三个特征
两直线平行
同位角相等
内错角相等
同旁内角互补
2. 直线平行的特征与直线平行的条件的区别。
(1)识别与特征的条件与结论有什么关系?
互换。
(2)使用识别时是已知 ___,说明________
角的相等或互补
两直线平行
使用特征时是已知 ,说明_____________
两直线平行
角的相等或互补
3. 几何中的计算往往要说理,要熟悉几何里计算题的格式,学
习合情说理。
作业
1. 习题2.4 知识技能1,2
2. 习题2.4 问题解决
谢谢合作!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
