七年级北师大版下册 2.2 探索直线平行的条件课件 (共36张PPT)
文档属性
| 名称 | 七年级北师大版下册 2.2 探索直线平行的条件课件 (共36张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-30 08:08:17 | ||
图片预览




文档简介
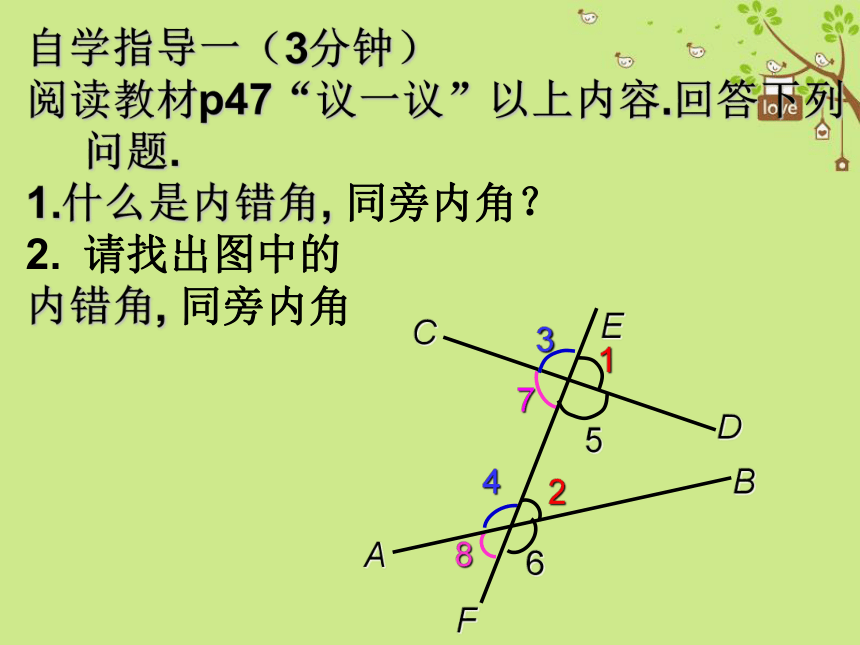
回顾与思考
1.指出图中的同位角。
2.根据上节课所学平行
公理哪些角相等可判定
直线CD和AB平行?
探索直线平行的条件2
学习目标(1分钟)
1 .探索直线平行的条件。
2.能根据直线平行的条件判定两直线平行。
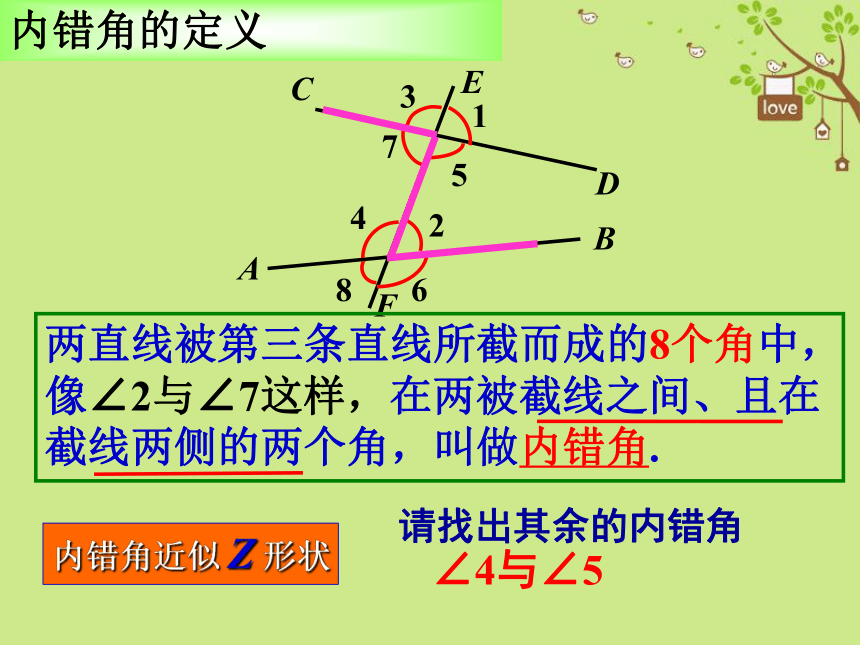
自学指导一(3分钟)
阅读教材p47“议一议”以上内容.回答下列问题.
1.什么是内错角, 同旁内角?
请找出图中的
内错角, 同旁内角
内错角近似 Z 形状
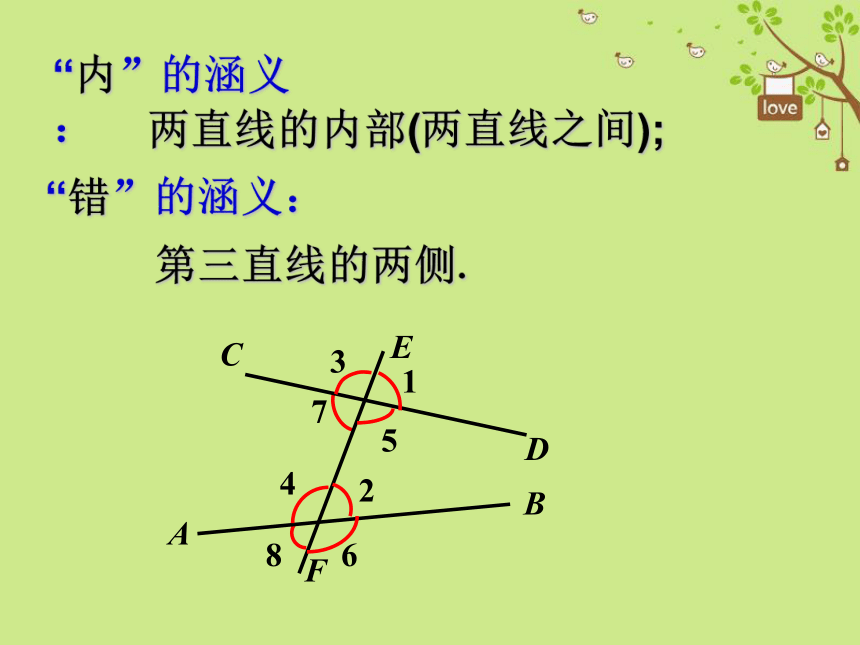
内错角的定义
两直线被第三条直线所截而成的8个角中, 像∠2与∠7这样,在两被截线之间、且在截线两侧的两个角,叫做内错角.
请找出其余的内错角
∠4与∠5
“内”的涵义:
两直线的内部(两直线之间);
“错”的涵义:
第三直线的两侧.
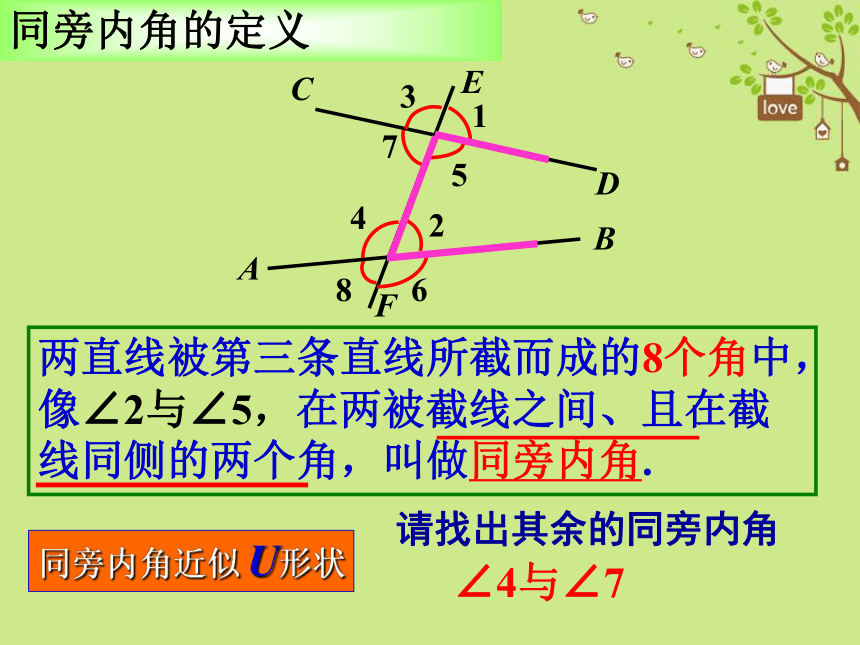
同旁内角的定义
同旁内角近似 U形状
两直线被第三条直线所截而成的8个角中, 像∠2与∠5,在两被截线之间、且在截线同侧的两个角,叫做同旁内角.
请找出其余的同旁内角
∠4与∠7
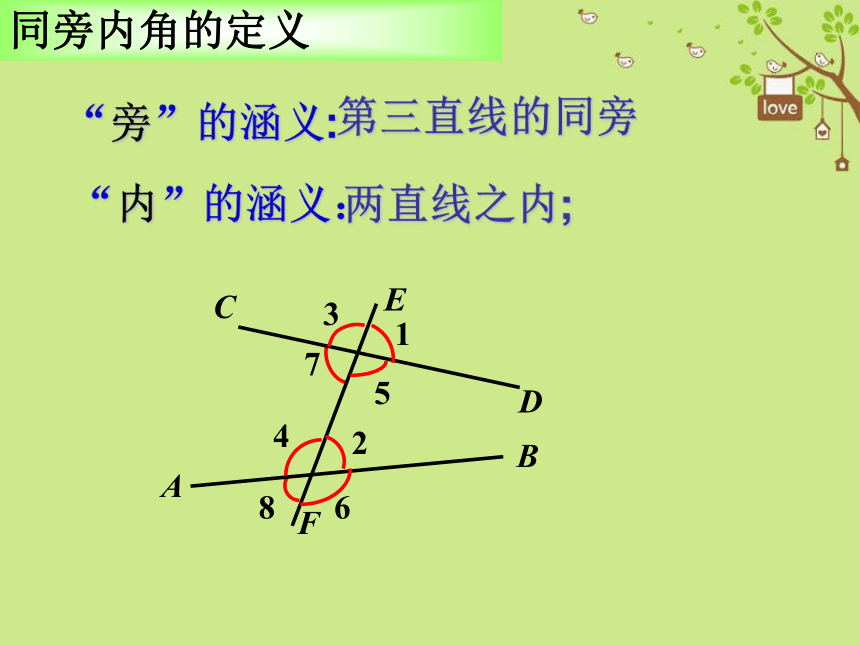
“内”的涵义:
“旁”的涵义:
两直线之内;
第三直线的同旁
同旁内角的定义
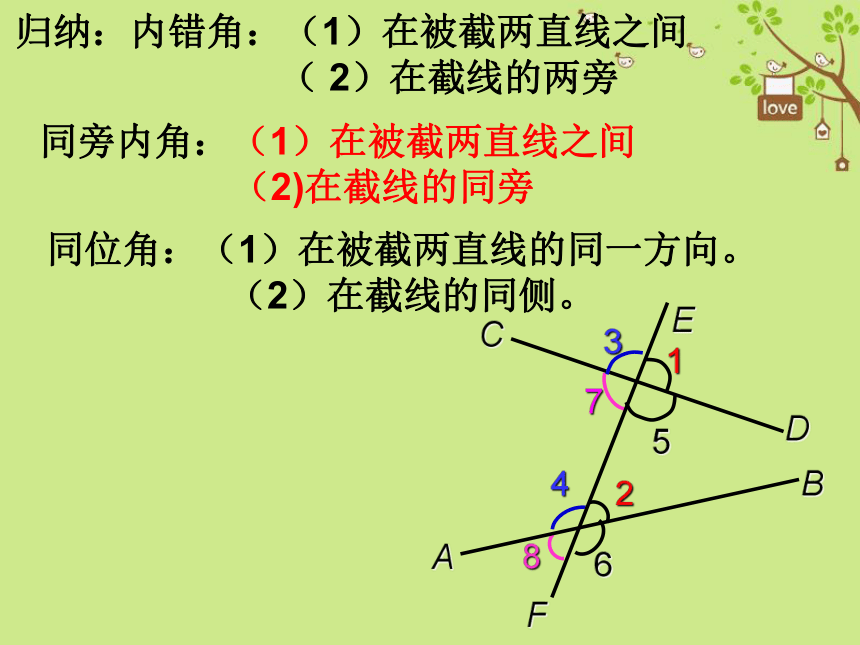
归纳:内错角:(1)在被截两直线之间
( 2)在截线的两旁
同旁内角:(1)在被截两直线之间
(2)在截线的同旁
同位角:(1)在被截两直线的同一方向。
(2)在截线的同侧。
自学检测1:(4分钟)
1.P48随堂练习T1
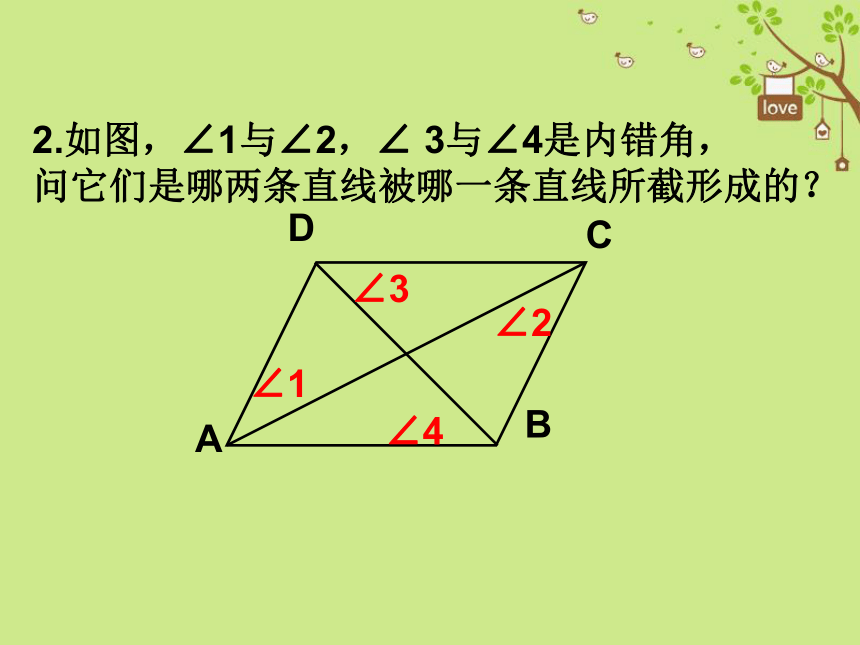
2.如图,∠1与∠2,∠ 3与∠4是内错角,
问它们是哪两条直线被哪一条直线所截形成的?
∠1
∠2
∠3
∠4
3.找出图中的同位角,内错角,同旁内角。
自学指导二:(5分钟)
阅读教材P47的“议一议”中的问题。
2. 同旁内角满足什么关系时?两直线平?为什么?
1. 内错角满足什么关系时?两直线平行?为什么?
两直线平行 的 判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
应用格式:
内错角相等,两直线平行
同旁内角互补,两直线平行
∴ a∥b
“内错角相等,两直线平行”
∵∠2=∠3
∴ a∥b
“同旁内角互补,两直线平行”
∵∠2+∠4 =180°
如何证明这两个定理?
内错角相等,两直线平行.
同旁内角互补,两直线平行.
(1)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
内错角 ∠1 = ∠2 .
证明思路
二直线平行
同位角相等
对顶角相等
内错角相等
自学检测2:(8分钟)
内错角相等,两直线平行.
(1)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
内错角 ∠1 = ∠2 .
证明: 设∠1 的对顶角是∠3,
∵∠3 = ∠1,
( )
对顶角相等
∠1 = ∠2, ( )
已知
∴ ∠3 = ∠2; ( )
∴ 直线 a∥b. ( ).
等量代换
同位角相等,两直线平行.
(2)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
同旁内角 ∠1 与∠2互补 .
同位角相等
1
同角的补角相等
证明思路
二直线平行
同旁内角互补,两直线平行.
(2)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
同旁内角 ∠1 与∠2互补 .
证明: 设∠1 的 ,
已知
∴ ∠3 ; ( )
∴ 直线 a∥b. ( ).
1
补角为∠3
= ∠2
同位角相等,两直线平行.
∵ ∠1 + ∠2= 180
同角的补角相等
∴ ∠1 +∠3=,180 °
B
C
D
A
E
图2—8
我是这样想的:
他选谁为第三线?
内错角相等,
两直线平行。
如图2—8,三个相同的三角尺拼成一个图形,请找出图中的一组平行线,并说明你的理由。
用的是什么角?
内错角。
你知道这一步的理由吗?
∠BCA=∠EAC,
BD∥AE。
AC
自学指导:三(4分钟)
B
C
D
A
E
图2—8
如图2—8,三个相同的三角尺拼成一个图形,请找出图中的一组平行线,并说明你的理由。
还有方法吗?
两直线平行的条件
(2)同位角相等,两直线平行.
(1)平行线定义;
(3)内错角相等,两直线平行.
(4)同旁内角互补,两直线平行.
(5)如果两条直线都和第三条直线平行,那么这两条直线也平行.
注:同位角,内错角,同旁内角均不是平行线所特有的.
1、观察右图并填空:
∠1 与 是同位角;
∠5 与 是同旁内角
(3) ∠1 与 是内错角;
b
a
n
m
2
3
1
4
5
∠4
∠3
当堂训练:(13分钟 )
∠2
3.如图7在下列四组条件中,能判定AB∥CD的是( )
A.∠1=∠2; B.∠3=∠4;
C.∠BAD+∠ABC=180°;
D.∠ABD=∠BDC
4.如图,直线a、b与直线c相交,给出下列条件:①∠1=∠2, ②∠3=∠6, ③∠4+∠7=180°, ④∠5+∠3=180°,其中能判断a∥b的是( )
A.①②③④ B.①③④ C.①③ D.②④
5.如图填空:
(1)∵∠2=∠3(已知)
∴ AB__________( )
(2)∵∠1=∠A(已知)
∴ __________( )
(3)∵∠1=∠D(已知)
∴ __________( )
(4)∵_______=∠F(已知)
∴ AC∥DF( )
6.填空。如图,∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=90°,∠______=90°( )
∴∠CAB=∠______( )
∵∠CAE=∠DBF(已知)
∴∠BAE=∠______
∴_____∥_____( )
7、已知,如图∠1+∠2=180°,填空。
∵∠1+∠2=180°( )
又∠2=∠3( )
∴∠1+∠3=180°
∴_________( )
8.如图,已知∠1与∠3互余,∠2与∠3的余角互补问直线平行吗?为什么?
9.如图,∠ABC=∠ADC、BF和DE是∠ABC、∠ ADC的角平分线,∠1=∠2,求证DC∥AB。
10.如图,∠B=∠C,B、A、D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,
求证:AE∥BC。
11、如图11,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。求证:AB∥CD,MP∥NQ.
12、已知:如图:∠AHF+∠FMD=180°,GH平分∠AHM,MN平分∠DMH。
求证:GH∥MN。
13、如图,已知:∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,
求证:CD∥BE。
14、如图,已知:∠A=∠1,∠C=∠2。求证:求证:AB∥CD。
1.指出图中的同位角。
2.根据上节课所学平行
公理哪些角相等可判定
直线CD和AB平行?
探索直线平行的条件2
学习目标(1分钟)
1 .探索直线平行的条件。
2.能根据直线平行的条件判定两直线平行。
自学指导一(3分钟)
阅读教材p47“议一议”以上内容.回答下列问题.
1.什么是内错角, 同旁内角?
请找出图中的
内错角, 同旁内角
内错角近似 Z 形状
内错角的定义
两直线被第三条直线所截而成的8个角中, 像∠2与∠7这样,在两被截线之间、且在截线两侧的两个角,叫做内错角.
请找出其余的内错角
∠4与∠5
“内”的涵义:
两直线的内部(两直线之间);
“错”的涵义:
第三直线的两侧.
同旁内角的定义
同旁内角近似 U形状
两直线被第三条直线所截而成的8个角中, 像∠2与∠5,在两被截线之间、且在截线同侧的两个角,叫做同旁内角.
请找出其余的同旁内角
∠4与∠7
“内”的涵义:
“旁”的涵义:
两直线之内;
第三直线的同旁
同旁内角的定义
归纳:内错角:(1)在被截两直线之间
( 2)在截线的两旁
同旁内角:(1)在被截两直线之间
(2)在截线的同旁
同位角:(1)在被截两直线的同一方向。
(2)在截线的同侧。
自学检测1:(4分钟)
1.P48随堂练习T1
2.如图,∠1与∠2,∠ 3与∠4是内错角,
问它们是哪两条直线被哪一条直线所截形成的?
∠1
∠2
∠3
∠4
3.找出图中的同位角,内错角,同旁内角。
自学指导二:(5分钟)
阅读教材P47的“议一议”中的问题。
2. 同旁内角满足什么关系时?两直线平?为什么?
1. 内错角满足什么关系时?两直线平行?为什么?
两直线平行 的 判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
应用格式:
内错角相等,两直线平行
同旁内角互补,两直线平行
∴ a∥b
“内错角相等,两直线平行”
∵∠2=∠3
∴ a∥b
“同旁内角互补,两直线平行”
∵∠2+∠4 =180°
如何证明这两个定理?
内错角相等,两直线平行.
同旁内角互补,两直线平行.
(1)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
内错角 ∠1 = ∠2 .
证明思路
二直线平行
同位角相等
对顶角相等
内错角相等
自学检测2:(8分钟)
内错角相等,两直线平行.
(1)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
内错角 ∠1 = ∠2 .
证明: 设∠1 的对顶角是∠3,
∵∠3 = ∠1,
( )
对顶角相等
∠1 = ∠2, ( )
已知
∴ ∠3 = ∠2; ( )
∴ 直线 a∥b. ( ).
等量代换
同位角相等,两直线平行.
(2)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
同旁内角 ∠1 与∠2互补 .
同位角相等
1
同角的补角相等
证明思路
二直线平行
同旁内角互补,两直线平行.
(2)已知: 如图 , 二直线a 、 b
b
a
被第三直线 c 所截,
求证: 直线 a∥b.
同旁内角 ∠1 与∠2互补 .
证明: 设∠1 的 ,
已知
∴ ∠3 ; ( )
∴ 直线 a∥b. ( ).
1
补角为∠3
= ∠2
同位角相等,两直线平行.
∵ ∠1 + ∠2= 180
同角的补角相等
∴ ∠1 +∠3=,180 °
B
C
D
A
E
图2—8
我是这样想的:
他选谁为第三线?
内错角相等,
两直线平行。
如图2—8,三个相同的三角尺拼成一个图形,请找出图中的一组平行线,并说明你的理由。
用的是什么角?
内错角。
你知道这一步的理由吗?
∠BCA=∠EAC,
BD∥AE。
AC
自学指导:三(4分钟)
B
C
D
A
E
图2—8
如图2—8,三个相同的三角尺拼成一个图形,请找出图中的一组平行线,并说明你的理由。
还有方法吗?
两直线平行的条件
(2)同位角相等,两直线平行.
(1)平行线定义;
(3)内错角相等,两直线平行.
(4)同旁内角互补,两直线平行.
(5)如果两条直线都和第三条直线平行,那么这两条直线也平行.
注:同位角,内错角,同旁内角均不是平行线所特有的.
1、观察右图并填空:
∠1 与 是同位角;
∠5 与 是同旁内角
(3) ∠1 与 是内错角;
b
a
n
m
2
3
1
4
5
∠4
∠3
当堂训练:(13分钟 )
∠2
3.如图7在下列四组条件中,能判定AB∥CD的是( )
A.∠1=∠2; B.∠3=∠4;
C.∠BAD+∠ABC=180°;
D.∠ABD=∠BDC
4.如图,直线a、b与直线c相交,给出下列条件:①∠1=∠2, ②∠3=∠6, ③∠4+∠7=180°, ④∠5+∠3=180°,其中能判断a∥b的是( )
A.①②③④ B.①③④ C.①③ D.②④
5.如图填空:
(1)∵∠2=∠3(已知)
∴ AB__________( )
(2)∵∠1=∠A(已知)
∴ __________( )
(3)∵∠1=∠D(已知)
∴ __________( )
(4)∵_______=∠F(已知)
∴ AC∥DF( )
6.填空。如图,∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=90°,∠______=90°( )
∴∠CAB=∠______( )
∵∠CAE=∠DBF(已知)
∴∠BAE=∠______
∴_____∥_____( )
7、已知,如图∠1+∠2=180°,填空。
∵∠1+∠2=180°( )
又∠2=∠3( )
∴∠1+∠3=180°
∴_________( )
8.如图,已知∠1与∠3互余,∠2与∠3的余角互补问直线平行吗?为什么?
9.如图,∠ABC=∠ADC、BF和DE是∠ABC、∠ ADC的角平分线,∠1=∠2,求证DC∥AB。
10.如图,∠B=∠C,B、A、D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,
求证:AE∥BC。
11、如图11,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。求证:AB∥CD,MP∥NQ.
12、已知:如图:∠AHF+∠FMD=180°,GH平分∠AHM,MN平分∠DMH。
求证:GH∥MN。
13、如图,已知:∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,
求证:CD∥BE。
14、如图,已知:∠A=∠1,∠C=∠2。求证:求证:AB∥CD。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
