人教版高一数学必修1 课件2.3幂函数(共18张PPT)
文档属性
| 名称 | 人教版高一数学必修1 课件2.3幂函数(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 367.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-29 00:00:00 | ||
图片预览





文档简介
第二章 基本初等函数(I)
2.3 幂函数
1. 记住幂函数的概念,能用描点法画出五个具体幂函数的图象;
2. 会用函数图象和代数运算的方法,探索幂函数的性质;
3. 会根据函数的性质,画幂函数大致图象并简单应用;
学习目标
独立自学
幂函数的定义:
一般地,我们把形如y=xα的函数叫做幂函数,
其中x为自变量, α为常数。
解析式 底数 指数 系数
幂函数 y=xα
指数函数 y=ax
(a>0且a≠1)
自变量x
独立自学
常数α
自变量x
常数a
1
1
练习
1. 下列函数是幂函数的是_________
(1) y= (2) y=2x2 (3) y=x2+x (4) y=1
(5) y= (6) y= (7) y=x0
2. 若y=mxα+(2n-4)是幂函数,则m=______n=_____.
1 2
引导探究
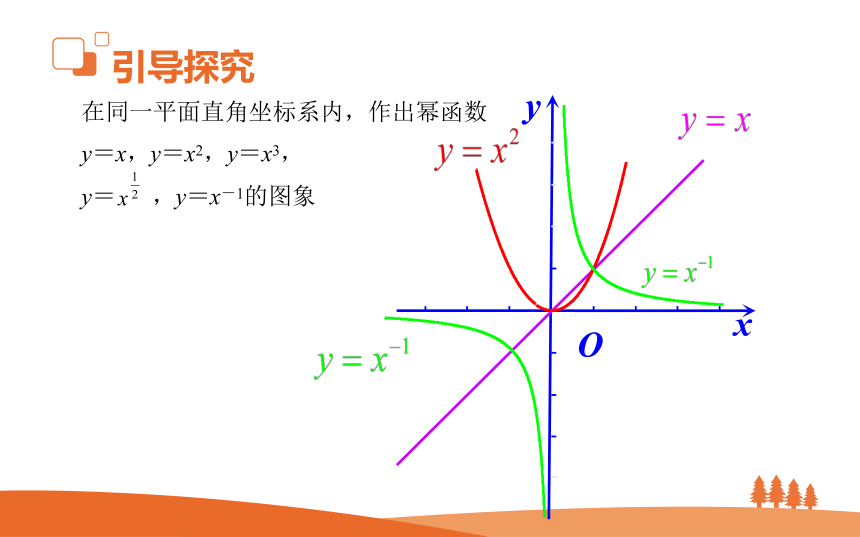
在同一平面直角坐标系内,作出幂函数
y=x,y=x2,y=x3,
y= ,y=x-1的图象
x
y
O
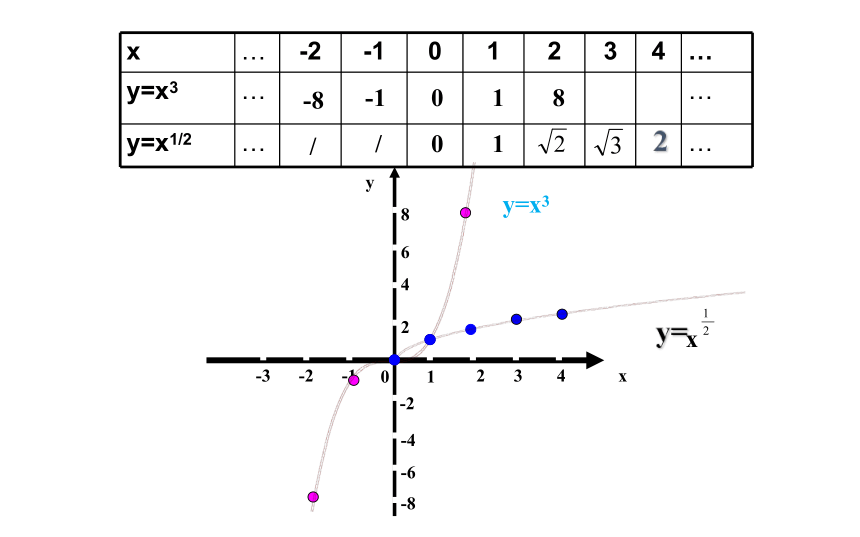
x … -2 -1 0 1 2 3 4 …
y=x3 … …
y=x1/2 … …
-8
-1
0
1
8
0
1
0
x
y
1
2
3
4
-1
-2
-3
2
4
6
8
-2
-4
-6
-8
y=x3
/
/
y=
x
2
引导探究
在同一平面直角坐标系内,作出幂函数
y=x,y=x2,y=x3,
y= ,y=x-1的图象
x
y
O
练习
y= x3 y=x -1
定义域
值 域
单调性
定点
y = x
R
R
[0,+∞)
R
R
[0,+∞)
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
在R上增
在(-∞,0]上减在(0, +∞)上增
在R上增
在(0,+∞)上增
在( -∞,0)上减在(0, +∞)上减
(1,1)
奇偶性
y = x2
R
[0,+∞)
幂函数y=xα在第一象限的图象特征
引导探究1
幂函数在(0,+∞)上的单调性
(1)如果α>0,幂函数y=xα在(0,+∞)上是增函数.
(2)如果α<0,幂函数y=xα在(0,+∞)上是减函数.
练习
如果不用描点法,如何画出 在定义域的大致图象?
引导探究2
(1)定义域
(2)奇偶性
提示:指数幂化为根式
引导探究3
(4)如图
利用单调性判断下列各值的大小。
(1)30.8 与 30.7
y= 3x在R上是增函数
∵0.8>0.7 ∴ 30.8 > 30.7
y=x 在(0,∞)上是减函数
∵3<3.1 ∴
典型例题
比较幂形式的两个数的大小,一般的思路是:
(1)若能化为同底,则用指数函数的单调性;
(2)若能化为同指,则用幂函数的单调性;
(3)若既不同指,也不同底,则用中间值法
利用幂函数单调性比较大小时
要注意比较大小的两个实数必须在同一单调区间内,
否则无法比较大小
幂函数
定义
五个特殊幂函数
图象
基本性质
一:掌握幂函数随着a的变化,图形的变化趋势以及性质
二:学会利用幂函数的性质解决各类问题,
如比较大小,陌生函数的图像问题等。
目标升华
