北师大版2019年春八年级数学下册第二章一元一次不等式与一元一次不等式组复习课课件(20张PPT)
文档属性
| 名称 | 北师大版2019年春八年级数学下册第二章一元一次不等式与一元一次不等式组复习课课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 577.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-30 23:01:25 | ||
图片预览






文档简介
课件20张PPT。BS八(下)
教学课件第二章 一元一次不等式与
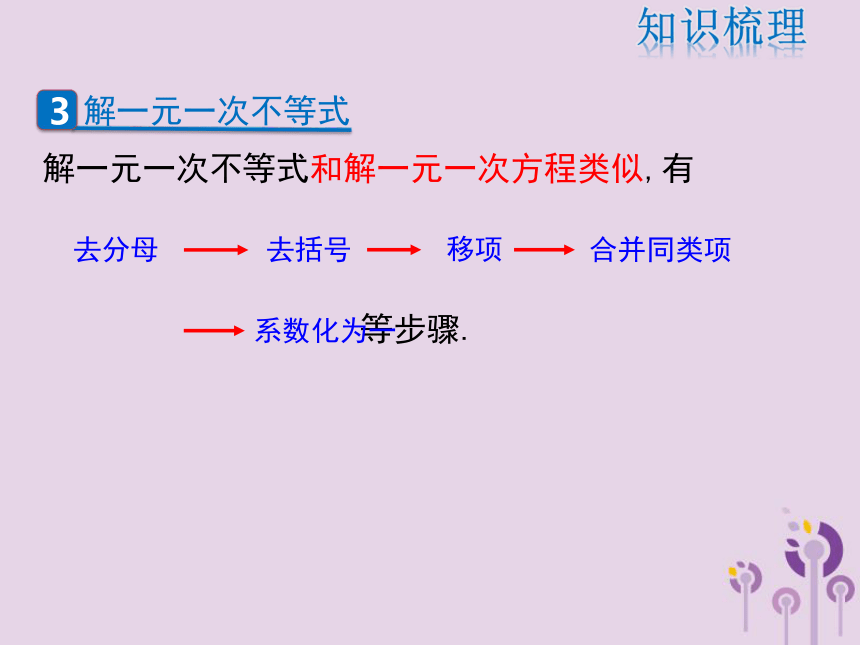
一元一次不等式组复习课 1.性质1:如果a>b,那么 a + c > ,且 a-c> .b + cb-c>><<4.不等式还具有传递性:如果a > b,b > c,那么a > c.不等号一元一次不等式一元一次不等式组不等式的解集不等式组的解集不等式知识梳理 解一元一次不等式和解一元一次方程类似,有
等步骤.
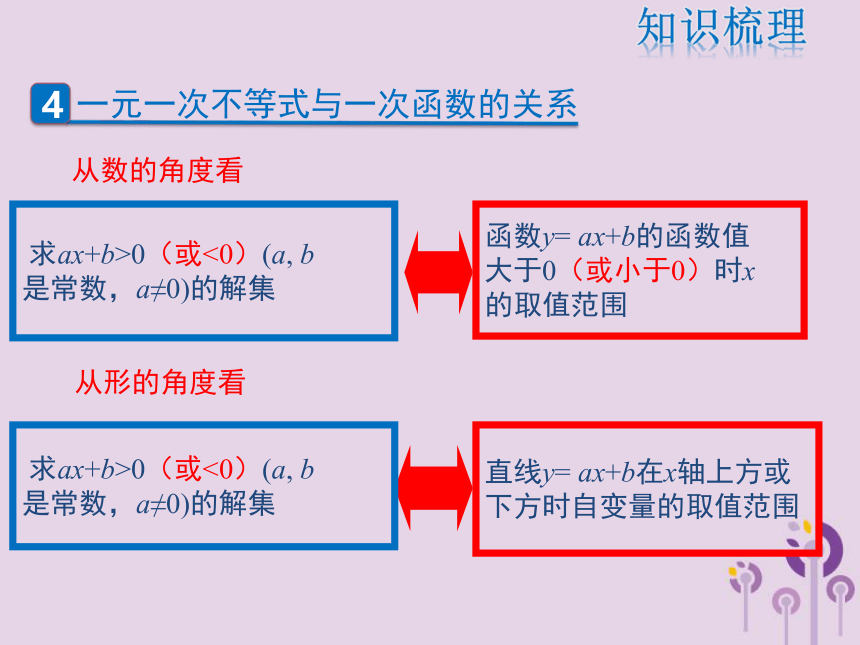
去分母去括号移项合并同类项系数化为一知识梳理 求ax+b>0(或<0)(a, b
是常数,a≠0)的解集函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围直线y= ax+b在x轴上方或
下方时自变量的取值范围从数的角度看从形的角度看 求ax+b>0(或<0)(a, b
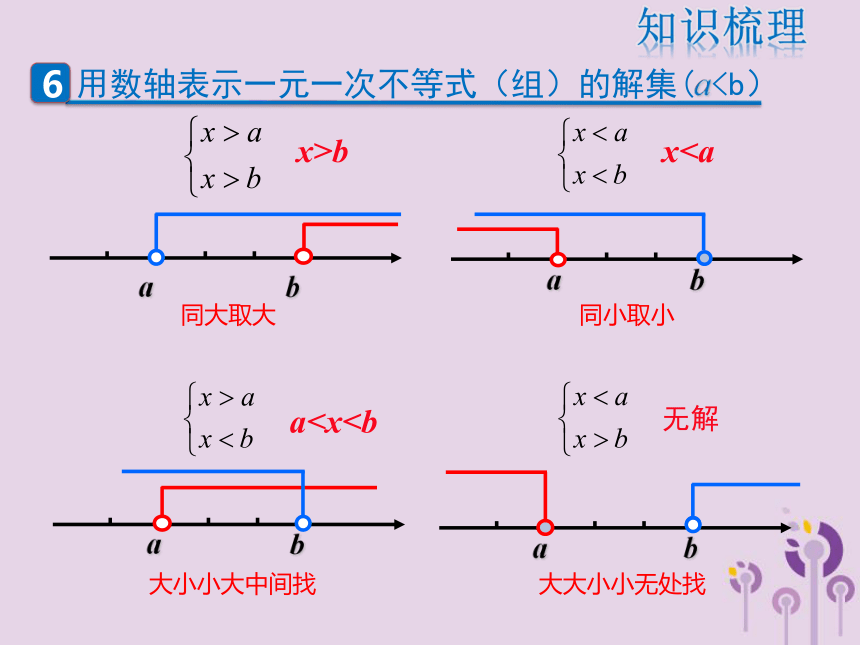
是常数,a≠0)的解集知识梳理1.分别求出不等式组中各个不等式的解集;
2.利用数轴求出这些不等式的解集的公共部分.知识梳理 同大取大 同小取小 大小小大中间找 大大小小无处找x>bx 或解集,并写出答案知识梳理 下列命题正确的是 ( )
A.若a>b,bc B.若a>b,则ac>bc
C.若a>b,则ac2>bc2 D.若ac2>bc2,则a>bD【解析】选项A,由a>b,bc ;选项B,a>b,当c=0时,ac=bc,不能根据不等式的性质确定ac>bc ;选项C,a>b,当c=0时,ac2=bc2,不能根据不等式的性质确定ac2>bc2;选项D,ac2>bc2,隐含c≠0 ,可以根据不等式的性质在不等式的两边同时除以正数c2,从而确定a>b.考点讲练例1 练习1:已知a A.3a<3b B.-3a<-3b
C.a-3∴当y<2时,x的取值范围是x<3.C考点讲练例3练习5:某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.>1500考点讲练练习6: 已知直线y=2x-b经过点(2,-2),求关于x的不等式2x-b≥0的解集.解:把点(2,-2)代入直线y=2x-b,
得-2=4-b,
解得 b=6.
故直线表达式为y=2x-6,
解得x≥3.考点讲练解:解不等式?,得 x≤3, 通过观察数轴可知该不等式组的整数解为2,3.考点讲练例4练习7:使不等式x-1≥2与3x-7<8同时成立的x的整数值是 . 3,4解题技巧:解一元一次不等式组,在找“公共部分”的过程中,可借助数轴或口诀确定不等式组的解集.C考点讲练 某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、6元.若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.解:设购买甲树苗的数量为x株,依题意得解得 x≥120. ∴购买甲树苗120株,乙树苗240株,此时费用最省.∵甲树苗比乙树苗每株多2元,
∴要节省费用,则要尽量少买甲树苗. 又x最小为120, 考点讲练例5解题技巧:解不等式的应用问题的步骤包括审、设、列、解、找、答这几个环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.考点讲练一元一次不等式(组)不等式不等式的解集一元一次不等式一元一次不等式组解集数轴表示不等式的基本性质解 集数轴表示解法解法实际应用与一次函数关系课堂小结
教学课件第二章 一元一次不等式与
一元一次不等式组复习课 1.性质1:如果a>b,那么 a + c > ,且 a-c> .b + cb-c>><<4.不等式还具有传递性:如果a > b,b > c,那么a > c.不等号一元一次不等式一元一次不等式组不等式的解集不等式组的解集不等式知识梳理 解一元一次不等式和解一元一次方程类似,有
等步骤.
去分母去括号移项合并同类项系数化为一知识梳理 求ax+b>0(或<0)(a, b
是常数,a≠0)的解集函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围直线y= ax+b在x轴上方或
下方时自变量的取值范围从数的角度看从形的角度看 求ax+b>0(或<0)(a, b
是常数,a≠0)的解集知识梳理1.分别求出不等式组中各个不等式的解集;
2.利用数轴求出这些不等式的解集的公共部分.知识梳理 同大取大 同小取小 大小小大中间找 大大小小无处找x>bx
A.若a>b,b
C.若a>b,则ac2>bc2 D.若ac2>bc2,则a>bD【解析】选项A,由a>b,b
C.a-3
得-2=4-b,
解得 b=6.
故直线表达式为y=2x-6,
解得x≥3.考点讲练解:解不等式?,得 x≤3, 通过观察数轴可知该不等式组的整数解为2,3.考点讲练例4练习7:使不等式x-1≥2与3x-7<8同时成立的x的整数值是 . 3,4解题技巧:解一元一次不等式组,在找“公共部分”的过程中,可借助数轴或口诀确定不等式组的解集.C考点讲练 某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、6元.若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.解:设购买甲树苗的数量为x株,依题意得解得 x≥120. ∴购买甲树苗120株,乙树苗240株,此时费用最省.∵甲树苗比乙树苗每株多2元,
∴要节省费用,则要尽量少买甲树苗. 又x最小为120, 考点讲练例5解题技巧:解不等式的应用问题的步骤包括审、设、列、解、找、答这几个环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.考点讲练一元一次不等式(组)不等式不等式的解集一元一次不等式一元一次不等式组解集数轴表示不等式的基本性质解 集数轴表示解法解法实际应用与一次函数关系课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
