四年级上册数学同步奥数课件第三讲 观察物体(数图形)苏教版 (共16张PPT)
文档属性
| 名称 | 四年级上册数学同步奥数课件第三讲 观察物体(数图形)苏教版 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 855.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-31 06:05:19 | ||
图片预览





文档简介
四年级同步奥数
第三讲
观察物体(数图形)
例题精学
例题1:数一数,下图有多少个正方形?(每个小方格是边长1的正方形)
思路分析:
1、边长为1的正方形有几个?
2、边长为2的正方形有几个?
3、边长为3的正方形有几个?
边长为1的正方形有 3×3=9个
边长为2的正方形有 2×2=4个
边长为3的正方形有 1×1=1个
共有9+4+1=14个正方形
知识点 1:根据正方形数正方形
如果正方形的边长包含的基本线段的条数是n,那么:
正方形的个数=1×1+2×2+……+n×n.
阶段总结:
同步精练
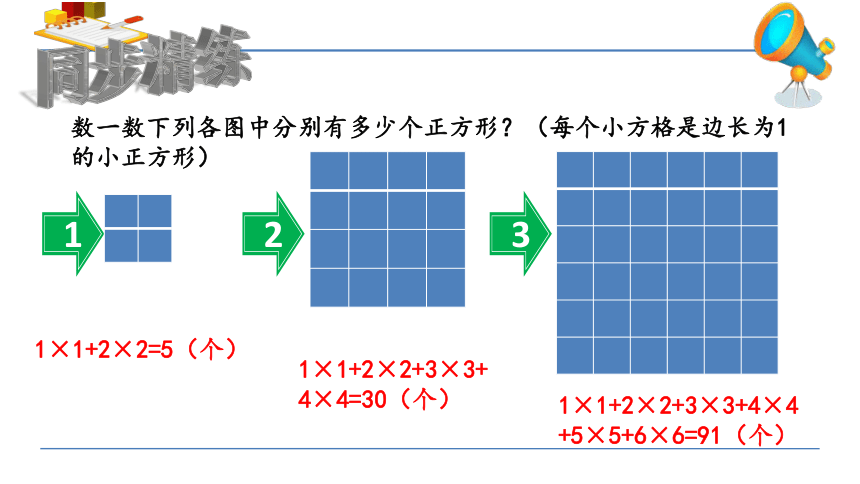
数一数下列各图中分别有多少个正方形?(每个小方格是边长为1的小正方形)
1
1×1+2×2=5(个)
2
1×1+2×2+3×3+4×4=30(个)
3
1×1+2×2+3×3+4×4+5×5+6×6=91(个)
例题精学
例题2:数一数,下图有多少个正方形?(每个小方格是边长1的正方形)
思路分析:
1、边长为1的正方形有几个?
2、边长为2的正方形有几个?
边长为1的正方形有3×2=6个
边长为2的正方形有2×1=2个
共有6+2=8个正方形
知识点 2:根据长方形数正方形
一般情况下,如果一个长方形的长被分成m等份,宽被分成n等份。长和宽的每一份都是相等的,那么正方形的总数为(nm×n+(m-1)×(n-1)+(m-2)×(n-2)+……+(m-n+1)×1 。
阶段总结:
同步精练
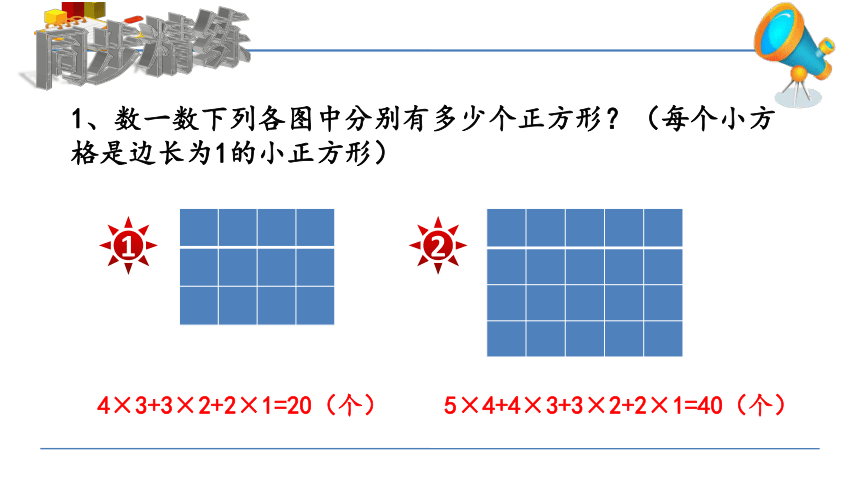
1、数一数下列各图中分别有多少个正方形?(每个小方格是边长为1的小正方形)
4×3+3×2+2×1=20(个)
1
2
5×4+4×3+3×2+2×1=40(个)
知识点 3:根据长方形数长方形
一般情况下,如果一个长方形的长被分成m等份,宽被分成n等份。长和宽的每一份都是相等的,那么长方形的总数为(nm×(m+1)÷2=a
n×(n+1)÷2=b
方形的总数为a×b。
复习回顾:
同步精练
2、下图中分别有多少个小长方形?多少个小正方形(每个小方格是边长为1的小正方形)
正方形:8×4+7×3+6×2+5×1=70(个)
长方形:
8×9÷2=36
4×5÷2=10
36×10=360(个)
例题精学:
例题3:数一数图中有多少个小正方体?
思路分析:
1、有几层?
2、一层有几个小正方体?
2×4=8(个)
知识点 4:数小正方体
1、分层
阶段总结:
2、数出每层的小正方体个数
3、求和
数一数图中分别有多少个小正方体?
思路分析:
1、有几层?
2、一层有几个小正方体?
12×3=36(个)
同步精练
例题精学
例题4:数一数图中共有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:1(个)
第二层:1+3=4(个)
第三层:4+5=9(个)
第四层:9+7=16(个)
共有
1+4+9+16=30(个)
数一数图中各有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:3(个)
第二层:3+3=6(个)
第三层:6+3=9(个)
第四层:9+3=12(个)
共有3+6+9+12=30(个)
1
同步精练
数一数图中各有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:6(个)
第二层:6+3=9(个)
第三层:9(个)
共有6+9+9=24(个)
2
同步精练
数一数图中各有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:8(个)
第二层:8+1=9(个)
第三层:9(个)
共有8+9+9=26(个)
3
同步精练
第三讲
观察物体(数图形)
例题精学
例题1:数一数,下图有多少个正方形?(每个小方格是边长1的正方形)
思路分析:
1、边长为1的正方形有几个?
2、边长为2的正方形有几个?
3、边长为3的正方形有几个?
边长为1的正方形有 3×3=9个
边长为2的正方形有 2×2=4个
边长为3的正方形有 1×1=1个
共有9+4+1=14个正方形
知识点 1:根据正方形数正方形
如果正方形的边长包含的基本线段的条数是n,那么:
正方形的个数=1×1+2×2+……+n×n.
阶段总结:
同步精练
数一数下列各图中分别有多少个正方形?(每个小方格是边长为1的小正方形)
1
1×1+2×2=5(个)
2
1×1+2×2+3×3+4×4=30(个)
3
1×1+2×2+3×3+4×4+5×5+6×6=91(个)
例题精学
例题2:数一数,下图有多少个正方形?(每个小方格是边长1的正方形)
思路分析:
1、边长为1的正方形有几个?
2、边长为2的正方形有几个?
边长为1的正方形有3×2=6个
边长为2的正方形有2×1=2个
共有6+2=8个正方形
知识点 2:根据长方形数正方形
一般情况下,如果一个长方形的长被分成m等份,宽被分成n等份。长和宽的每一份都是相等的,那么正方形的总数为(n
阶段总结:
同步精练
1、数一数下列各图中分别有多少个正方形?(每个小方格是边长为1的小正方形)
4×3+3×2+2×1=20(个)
1
2
5×4+4×3+3×2+2×1=40(个)
知识点 3:根据长方形数长方形
一般情况下,如果一个长方形的长被分成m等份,宽被分成n等份。长和宽的每一份都是相等的,那么长方形的总数为(n
n×(n+1)÷2=b
方形的总数为a×b。
复习回顾:
同步精练
2、下图中分别有多少个小长方形?多少个小正方形(每个小方格是边长为1的小正方形)
正方形:8×4+7×3+6×2+5×1=70(个)
长方形:
8×9÷2=36
4×5÷2=10
36×10=360(个)
例题精学:
例题3:数一数图中有多少个小正方体?
思路分析:
1、有几层?
2、一层有几个小正方体?
2×4=8(个)
知识点 4:数小正方体
1、分层
阶段总结:
2、数出每层的小正方体个数
3、求和
数一数图中分别有多少个小正方体?
思路分析:
1、有几层?
2、一层有几个小正方体?
12×3=36(个)
同步精练
例题精学
例题4:数一数图中共有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:1(个)
第二层:1+3=4(个)
第三层:4+5=9(个)
第四层:9+7=16(个)
共有
1+4+9+16=30(个)
数一数图中各有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:3(个)
第二层:3+3=6(个)
第三层:6+3=9(个)
第四层:9+3=12(个)
共有3+6+9+12=30(个)
1
同步精练
数一数图中各有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:6(个)
第二层:6+3=9(个)
第三层:9(个)
共有6+9+9=24(个)
2
同步精练
数一数图中各有多少个小正方体?
思路分析:
1、有几层?
2、每层各有几个小正方体?
3、下一层比上一层有什么变化?
第一层:8(个)
第二层:8+1=9(个)
第三层:9(个)
共有8+9+9=26(个)
3
同步精练
