7.10 能量守恒定律综合提高 word版含答案
文档属性
| 名称 | 7.10 能量守恒定律综合提高 word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 517.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-30 00:00:00 | ||
图片预览

文档简介
人教版物理必修2-第七章——能量守恒定律综合提高
(
能量守恒定律与功能关系
)
(
知识点睛
)
1.能量守恒定律
⑴ 内容:能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为另一种形式,或者从一个物体转移到另一个物体,在转化和转移的过程中,能量的总量保持不变。
⑵ 对能量守恒定律的理解
① 某种形式的能量减少,一定存在其他形式的能量增加,且增加量和减少量一定相等。
② 某个物体的能量减少,一定存在其他物体的能量增加,且增加量和减少量一定相等。
⑶ 表达式:① 或 ②
应用能量守恒的关键是分析清楚系统中有多少种形式的能量,发生了哪些转化和转移过程,再利用能量守恒定律求解。
2.功和能的区别与联系
⑴ 区别:功是过程量,能量是状态量。只能说处于某一状态的物体具有多少能量,而不能说这个物体(或系统)具有多少功。功和能是两个不同的概念。
⑵ 联系:功是能量转化的量度
① 不同形式的能量之间的转化通过做功来实现,即做功的过程是能量转化的过程
② 做了多少功就有多少能量发生了转化,功的正、负表示能量的转化方向。
3.常用的功能关系
⑴ 重力做功重力势能
重力做正功,重力势能减少;重力做负功(克服重力做功),重力势能增加。即
⑵ 弹簧弹力做功弹性势能
弹簧弹力做正功,弹性势能减少;弹簧弹力做负功(克服弹力做功),弹性势能增加。即
⑶ 合外力做功动能(对单个质点)
合外力做功等于物体动能变化,即动能定理。
⑷ 除重力和弹簧弹力之外的力做功机械能
除重力(或万有引力)、弹簧弹力之外,其他所有力对系统所做的功等于系统机械能的增量,即功能原理。即。
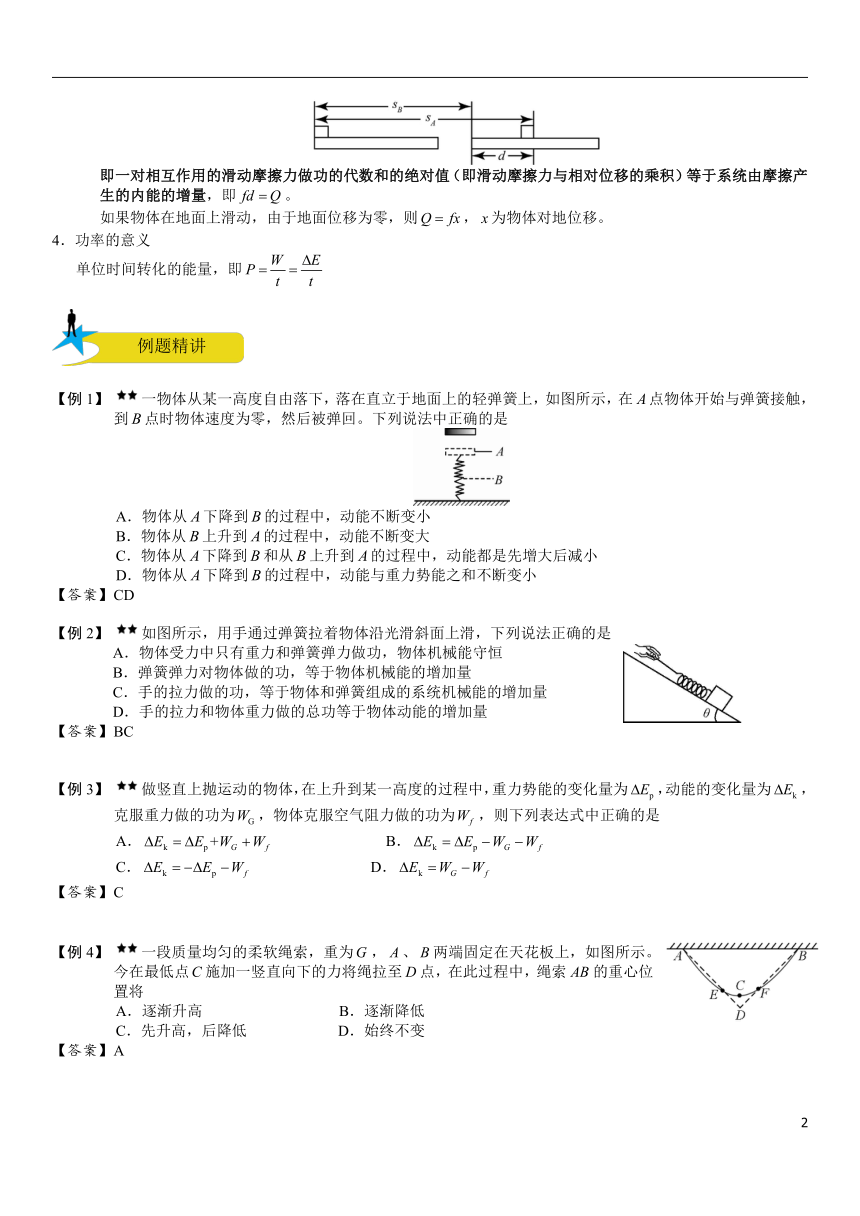
⑸ 一对相互作用的滑动摩擦力做功的代数和内能
以下图所示情景为例,质量为的木板静止于光滑水平面上,质量为的物块以初速度滑上木板,、接触面粗糙,经过一段时间,、位移分别为、,速度分别为、。
对物块应用动能定理:
对木板应用动能定理:
两式相加可得:,即①
根据能量守恒定律:在此过程中损失的动能转化为内能,即②
联立①②可得:
即一对相互作用的滑动摩擦力做功的代数和的绝对值(即滑动摩擦力与相对位移的乘积)等于系统由摩擦产生的内能的增量,即。
如果物体在地面上滑动,由于地面位移为零,则,为物体对地位移。
4.功率的意义
单位时间转化的能量,即
(
例题精讲
)
一物体从某一高度自由落下,落在直立于地面上的轻弹簧上,如图所示,在点物体开始与弹簧接触,到点时物体速度为零,然后被弹回。下列说法中正确的是
A.物体从下降到的过程中,动能不断变小
B.物体从上升到的过程中,动能不断变大
C.物体从下降到和从上升到的过程中,动能都是先增大后减小
D.物体从下降到的过程中,动能与重力势能之和不断变小
CD
如图所示,用手通过弹簧拉着物体沿光滑斜面上滑,下列说法正确的是
A.物体受力中只有重力和弹簧弹力做功,物体机械能守恒
B.弹簧弹力对物体做的功,等于物体机械能的增加量
C.手的拉力做的功,等于物体和弹簧组成的系统机械能的增加量
D.手的拉力和物体重力做的总功等于物体动能的增加量
BC
做竖直上抛运动的物体,在上升到某一高度的过程中,重力势能的变化量为,动能的变化量为,克服重力做的功为,物体克服空气阻力做的功为,则下列表达式中正确的是
A. B.
C. D.
C
一段质量均匀的柔软绳索,重为,、两端固定在天花板上,如图所示。今在最低点施加一竖直向下的力将绳拉至点,在此过程中,绳索的重心位置将
A.逐渐升高 B.逐渐降低
C.先升高,后降低 D.始终不变
A
如图所示,一轻质弹簧原长,竖直固定在水平面上,一质量为的小球从离水平面高为处自由下落,正好压在弹簧上,下落过程中小球遇到的空气阻力恒为,小球压缩弹簧的最大压缩量为。则弹簧被压到最短时的弹性势能为:
A.
B.
C.
D.
A
将质量为,边长为的匀质正方体翻到,若连续翻次,则推力至少做功为
A. B. C. D.
C
电机带动水平传送带以速度匀速传动,一质量为的小木块由静止轻放在传送带上,若小木块与传送带之间的动摩擦因数为,如图所示,当小木块与传送带相对静止时,求:
⑴ 小木块的位移;
⑵ 传送带转过的路程;
⑶ 摩擦过程产生的热量;
⑷ 电机带动传送带匀速转动输出的总能量。
⑴ ⑵ ⑶ ⑷
工厂流水线上采用弹射装置把物品转运,现简化其模型分析:如图所示,质量为的滑块,放在光滑的水平平台上,平台右端与水平传送带相接,传送带的运行速度为,长为;现将滑块向左压缩固定在平台上的轻弹簧,到达某处时由静止释放,若滑块离开弹簧时的速度小于传送带的速度,当滑块滑到传送带右端时,恰好与传送带速度相同,滑块与传送带间的动摩擦因数为求:
⑴ 释放滑块时,弹簧具有的弹性势能;
⑵ 滑块在传送带上滑行的整个过程中产生的热量。
⑴
⑵
在光滑的水平面上有一个质量长木板正以的速度向右运动,此时一个质量的小物块以速度从长木板的最右端冲上长木板,最终两个物体相对静止且物块没有滑下木板,板块之间的摩擦因数,求在此过程中产生的热量;
长木板放在光滑的水平面上,质量为的物块以水平初速度从一端滑上的水平上表面,它们在运动过程中的图象如图所示。则根据图中所给出的已知数据及物块质量,可以求出的物理量是
A.木板获得的动能
B.组成的系统损失的机械能
C.木板的最小长度
D.之间的动摩擦因数
C
如图所示,在水平桌面上的边角处有一轻质光滑的定滑轮,一条不可伸长的轻绳绕过定滑轮分别与物块相连,的质量分别为和,开始时系统处于静止状态,现用一水平恒力拉物块,使物块上升。已知当上升距离为时,的速度为,求此过程中物块克服摩擦力所做的功。(重力加速度为)
****************************************************************************************
如图所示,竖直平面内放一直角杆,杆的水平部分粗糙,动摩擦因数,杆的竖直部分光滑。两部分各套有质量均为的小球和,、球间用细绳相连。初始、均处于静止状态,已知:,。若球在水平拉力的作用下向右缓慢地移动(取),那么该过程中拉力做的功为
A. B. C. D.
A
****************************************************************************************
质量为的小球用长为的细线系于点,现将小球拉至点右上方与水平面成角的位置,此时细绳恰好伸直,并以竖直向下的初速度将小球抛出,求小球从点运动到最低点的过程中,线的拉力对小球做的功。
****************************************************************************************
一质量为的质点,系于长为的轻绳的一端,绳的另一端固定在点,假定绳是不可伸长的、柔软且无弹性的。今把质点从点的正上方离点的距离为的点以水平的速度抛出,如图。试求:
⑴ 轻绳即将伸直时,绳与竖直方向的夹角;
⑵ 当质点到达点的正下方时,绳对质点的拉力。
⑴ ⑵
****************************************************************************************
如图所示是利用潮汐发电的示意图,左方为陆地和海湾,中间的水坝下有通道,水经通道可带动发电机。涨潮时,水进入海湾,待内外水面高度相同,堵住通道,如图甲。潮落至最低点时放水发电,如图乙。待内外水面高度相同,再堵住通道,直至下次涨潮至最高点,又放水发电,如图丙。设海湾平均面积,高潮与低潮间高度差为,求一天内水流的平均功率。(取)
某辆以蓄电池为驱动能源的环保汽车,总质量。当它在水平路面上以的速度匀速行驶时,驱动电机的输入功率为,在此行驶状态下。
⑴ 若驱动电机能够将输入功率的转化为用于牵引汽车前进的机械功率,求汽车所受阻力与车重的比值(取);
⑵ 设想改用太阳能电池给该车供电,其他条件不变,求所需太阳能电池板的最小面积。结合计算结果,简述你对该设想的思考。
已知太阳辐射的总功率,太阳到地球的距离,太阳光传播到达地面的过程中大约有30%的能量损耗,该车所用太阳能电池的能量转化效率约为。
⑴ ⑵
(
1
)
