5.2三角形的三边关系 课件(共55张PPT)
文档属性
| 名称 | 5.2三角形的三边关系 课件(共55张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-31 00:00:00 | ||
图片预览








文档简介
课件55张PPT。三角形三边关系两条线段长度之和小于第三条
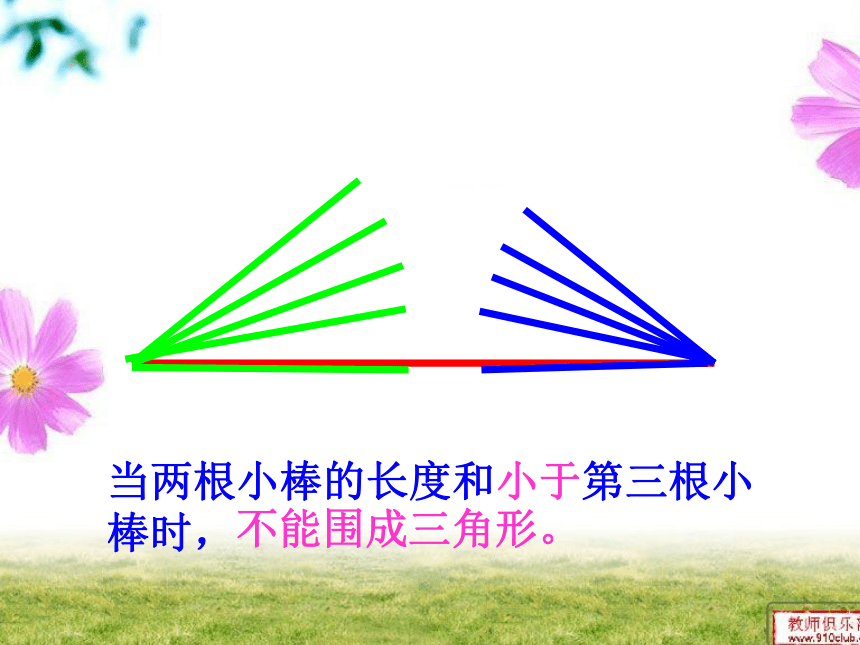
两条线段长度之和小于第三条不能围成三角形当两根小棒的长度和小于第三根小棒时,不能围成三角形。当两根小棒的长度和大于第三根小棒时,能围成三角形。猜想1:当两根小棒的长度和等于第三根小棒时,能围成三角形。猜想2:当两根小棒的长度和等于第三根小棒时,
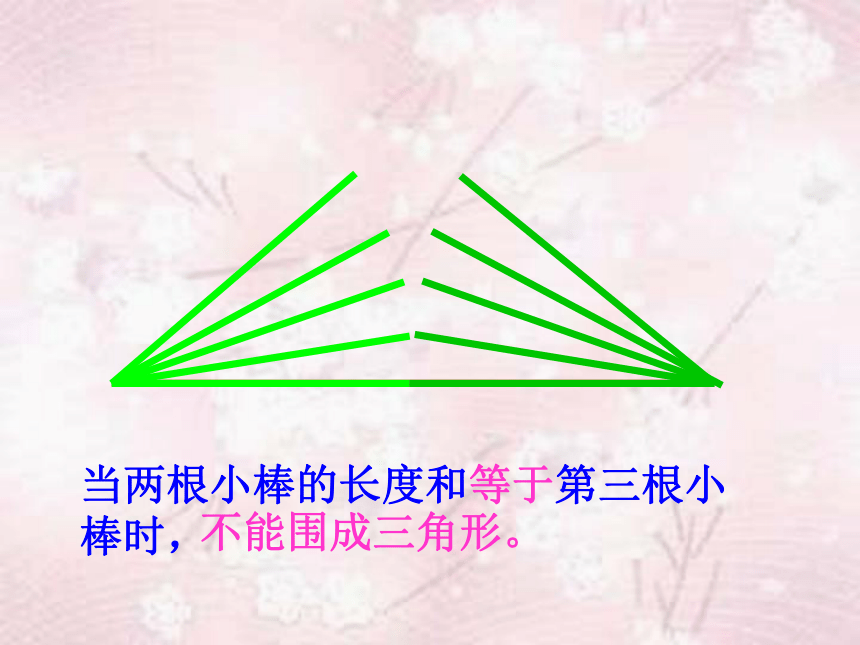
不能围成三角形。两条线段长度之和等于第三条当两根小棒的长度和等于第三根小棒时,不能 围成三角形
45ABC已知:AB=9有两条线段长度之和等于第三条不能围成三角形在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
1、3cm ,8cm, 5cm ( )
× 因为 3 + 5 = 8,
所以不能围成三角形。 两条线段长度之和大于第三条线段
两条线段长度之和大于第三条线段可以围成三角形在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
6cm ,4cm, 3cm ( )
√因为 6+4>3
6+3>4
4+3>6
所以能围成三角形。6cm, 4cm, 3cm在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
3、7cm ,15cm, 9cm ( )
√因为 7 + 9 > 15,
所以能围成三角形。用一根木棒做一个三角形的架子,怎么办? 鲁 班 有两根树干,一根长12米,另一根长8米,要做一个三角形屋架。请你想一想,第三根树干可能有多长?议一议:第三根树干的长度1、已知两条线段的长分别是3cm、5cm ,要想拼成一个三角形,问第三条线段a应 取的范围是多少?且第三条线段a的 长为奇数,问第三条线段应取多少长? (三)试一试:2cm反之:在三条线段中若 任两线段之和大于第三线段则这三条线段能构成一个三角形。理一理1、下面的三条线段可以围成一个三角形吗?能的打“√”
(单位:厘米)
432( )考考你:√下面的三条线段可以围成一个三角形吗? (单位:厘米)
×下面的三条线段可以围成一个三角形吗? (单位:厘米)
3( )√33在能拼成三角形的各组小棒下面画“√”第三条边多长才好?×√√√下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm
(2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm
(4) 4cm、5cm、6cm四.练习
(一)练一练只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形. (2) 因为4cm+5cm<10cm,
所以这三条线段不能组成一个三角形. (3) 因为3cm+5cm=8cm,
所以这三条线段不能组成一个三角形.练一练 (4) 因为4cm+5cm>6cm,
所以这三条线段能组成一个三角形.一.实验 准备好长度分别为:4cm,6cm,10cm,12cm的牙签各一根,从中任取三根看都能不能摆成一个三角形?从4根中取出3根有以下几种情况:(1)4cm,6cm,10cm通过动手发现: (3) (4) 可以摆成三角形,
(1) (2) 不能摆成三角形。通过实验你能发现
构成一个三角形的三边有什么规律?(2)4cm,6cm,12cm(3)4cm,10cm,12cm(4)6cm,10cm,12cm(四)做一做:1、已知两条边长分别为3cm、5cm,你可以画出几个符合条件的等腰三角形?并求符合条件的等腰三角形的周长. (3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.(二)判断:“摘苹果”(1)任何三条线段都能组成一个三角形 ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形( )(4)已知等腰三角形的两边长分别为8cm,3cm,
则这三角形的周长为 ( ) (A) 14cm (B)19cm
(C) 14cm或19cm (D) 不确定 ××2B3、请你设计。
公路两侧有A、B两个村子(如图),现在要在公路上修建一个公共汽车站,让这两个村子的人都能最省时、最方便。请问,公共汽车C应建在什么地方?ABC 小明想要给他的小狗做一个房子,房顶的框架是三角形的,其中一根木条是3分米,另一根是5分米,那么第三根木条可以是多少分米呢?(取整分米数) d o g
5 3 35 3 4 5 3 55 3 65 3 7535353你认为最有可能是哪种?√ 用长度为2cm、2cm、6cm、6cm、6cm这五条线段中的任意三条线段拼成一个三角形,你能拼成几种不同的形状? 666662学了这节课你有什么收获? 收获很多1.1.1.2.3.!!!我学会了 3、三角形的稳定性1、三角形的三边关系定理;(2)确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
三角形的任何两边的和大于第三边。
不能围成三角形。两条线段长度之和等于第三条当两根小棒的长度和等于第三根小棒时,不能 围成三角形
45ABC已知:AB=9有两条线段长度之和等于第三条不能围成三角形在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
1、3cm ,8cm, 5cm ( )
× 因为 3 + 5 = 8,
所以不能围成三角形。 两条线段长度之和大于第三条线段
两条线段长度之和大于第三条线段可以围成三角形在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
6cm ,4cm, 3cm ( )
√因为 6+4>3
6+3>4
4+3>6
所以能围成三角形。6cm, 4cm, 3cm在能围成三角形的一组线段后面打√,不能围成的打×。(用手势判断)
3、7cm ,15cm, 9cm ( )
√因为 7 + 9 > 15,
所以能围成三角形。用一根木棒做一个三角形的架子,怎么办? 鲁 班 有两根树干,一根长12米,另一根长8米,要做一个三角形屋架。请你想一想,第三根树干可能有多长?议一议:第三根树干的长度1、已知两条线段的长分别是3cm、5cm ,要想拼成一个三角形,问第三条线段a应 取的范围是多少?且第三条线段a的 长为奇数,问第三条线段应取多少长? (三)试一试:2cm
(单位:厘米)
432( )考考你:√下面的三条线段可以围成一个三角形吗? (单位:厘米)
×下面的三条线段可以围成一个三角形吗? (单位:厘米)
3( )√33在能拼成三角形的各组小棒下面画“√”第三条边多长才好?×√√√下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm
(2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm
(4) 4cm、5cm、6cm四.练习
(一)练一练只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形. (2) 因为4cm+5cm<10cm,
所以这三条线段不能组成一个三角形. (3) 因为3cm+5cm=8cm,
所以这三条线段不能组成一个三角形.练一练 (4) 因为4cm+5cm>6cm,
所以这三条线段能组成一个三角形.一.实验 准备好长度分别为:4cm,6cm,10cm,12cm的牙签各一根,从中任取三根看都能不能摆成一个三角形?从4根中取出3根有以下几种情况:(1)4cm,6cm,10cm通过动手发现: (3) (4) 可以摆成三角形,
(1) (2) 不能摆成三角形。通过实验你能发现
构成一个三角形的三边有什么规律?(2)4cm,6cm,12cm(3)4cm,10cm,12cm(4)6cm,10cm,12cm(四)做一做:1、已知两条边长分别为3cm、5cm,你可以画出几个符合条件的等腰三角形?并求符合条件的等腰三角形的周长. (3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.(二)判断:“摘苹果”(1)任何三条线段都能组成一个三角形 ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形( )(4)已知等腰三角形的两边长分别为8cm,3cm,
则这三角形的周长为 ( ) (A) 14cm (B)19cm
(C) 14cm或19cm (D) 不确定 ××2B3、请你设计。
公路两侧有A、B两个村子(如图),现在要在公路上修建一个公共汽车站,让这两个村子的人都能最省时、最方便。请问,公共汽车C应建在什么地方?ABC 小明想要给他的小狗做一个房子,房顶的框架是三角形的,其中一根木条是3分米,另一根是5分米,那么第三根木条可以是多少分米呢?(取整分米数) d o g
5 3 35 3 4 5 3 55 3 65 3 7535353你认为最有可能是哪种?√ 用长度为2cm、2cm、6cm、6cm、6cm这五条线段中的任意三条线段拼成一个三角形,你能拼成几种不同的形状? 666662学了这节课你有什么收获? 收获很多1.1.1.2.3.!!!我学会了 3、三角形的稳定性1、三角形的三边关系定理;(2)确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
三角形的任何两边的和大于第三边。
