八年级下册数学18.1平行四边形基础知识测试卷(含答案)
文档属性
| 名称 | 八年级下册数学18.1平行四边形基础知识测试卷(含答案) | 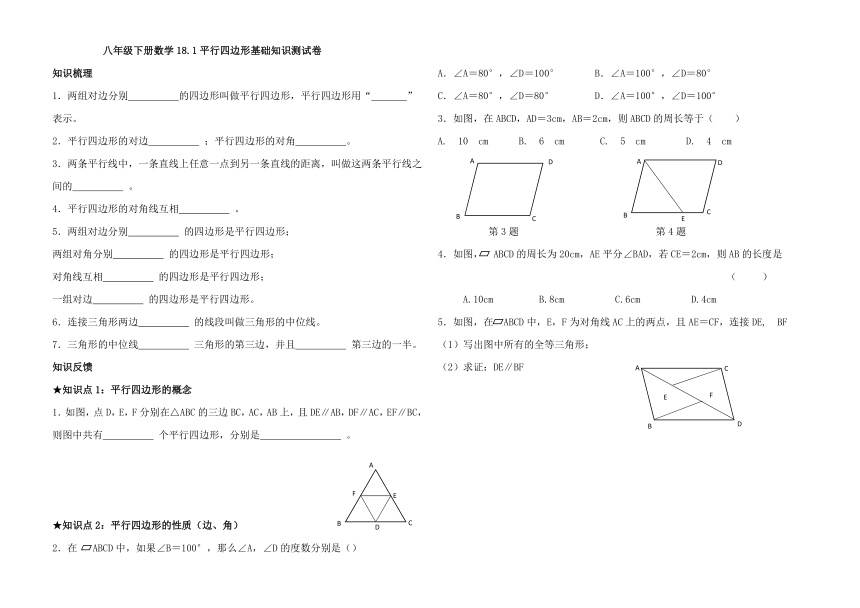 | |
| 格式 | zip | ||
| 文件大小 | 508.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-02 10:32:36 | ||
图片预览

文档简介
八年级下册数学18.1平行四边形基础知识测试卷
知识梳理
两组对边分别 的四边形叫做平行四边形,平行四边形用“ ”
表示。
2.平行四边形的对边 ;平行四边形的对角 。
3.两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的 。
4.平行四边形的对角线互相 。
5.两组对边分别 的四边形是平行四边形;
两组对角分别 的四边形是平行四边形;
对角线互相 的四边形是平行四边形;
一组对边 的四边形是平行四边形。
6.连接三角形两边 的线段叫做三角形的中位线。
7.三角形的中位线 三角形的第三边,并且 第三边的一半。
知识反馈
★知识点1:平行四边形的概念
1.如图,点D,E,F分别在△ABC的三边BC,AC,AB上,且DE∥AB,DF∥AC,EF∥BC,则图中共有 个平行四边形,分别是 。
★知识点2:平行四边形的性质(边、角)
2.在 ABCD中,如果∠B=100°,那么∠A,∠D的度数分别是()
A.∠A=80°,∠D=100° B.∠A=100°,∠D=80°
C.∠A=80°,∠D=80° D.∠A=100°,∠D=100°
3.如图,在ABCD,AD=3cm,AB=2cm,则ABCD的周长等于( )
A.?10?cm B.?6?cm C.?5?cm D.?4?cm
第3题 第4题
4.如图, ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是
( )
A.10cm B.8cm C.6cm D.4cm
5.如图,在 ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,?BF
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF
★知识点3:两条平行线之间的距离
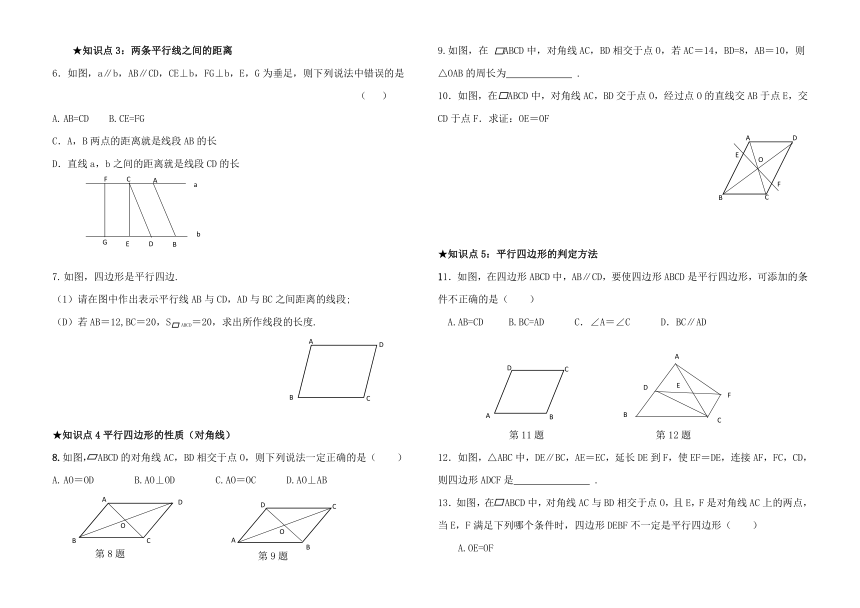
6.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G为垂足,则下列说法中错误的是
( )
AB=CD B.CE=FG
C.A,B两点的距离就是线段AB的长
D.直线a,b之间的距离就是线段CD的长
如图,四边形是平行四边.
(1)请在图中作出表示平行线AB与CD,AD与BC之间距离的线段;
(D)若AB=12,BC=20,S ABCD=20,求出所作线段的长度.
★知识点4平行四边形的性质(对角线)
8.如图, ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
AO=OD B.AO⊥OD? C.AO=OC D.AO⊥AB
9.如图,在 ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△OAB的周长为 .
10.如图,在 ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于点E,交CD于点F.求证:OE=OF
★知识点5:平行四边形的判定方法
11.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD B.BC=AD C.∠A=∠C D.BC∥AD
第11题 第12题
12.如图,△ABC中,DE∥BC,AE=EC,延长DE到F,使EF=DE,连接AF,FC,CD,则四边形ADCF是 .
13.如图,在 ABCD中,对角线AC与BD相交于点O,且E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
A.OE=OF
B.DE=BF
C.∠ADE=∠CBF
D.∠ABE=∠CDF
14.如图所示,在 ABCD中,AE,CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形.
如图所示,AB,CD相交于点O,AC∥DB,AO=BO.点E,F分别是OC,OD的中点.求证:
(1)△AOC≌△BOD
(2)四边形AFBE是平行四边形
如图,在 ABCD中,BF=DE,FG⊥AB于点G,EH⊥CD于点H,GH与BD交于点O.求证:GH与BD互相平分.
★知识点6:三角形的中位线及其定理
17.如图,D,E分别是△ABC的边AB,AC的中点,则△ABC的中位线是( )
A.线段DE B.线段CD C.线段BE D.以上答案都不对
第17题 第19题
18.已知△ABC的周长为40cm,中位线DE=6cm,EF=8cm,则另一条中位线DF的长是( )
A.4cm B.5cm C.6cm D.8cm
19.如图, ABCD的对角线AC,BD相交于点O,点E是CD的中点,若AD=4cm,则OE的长为 cm.
20.如图,已知DE为△ABC的中位线,延长DE到F,使EF=DE.
求证:四边形BCFD为平行四边形。
参 考 答 案
知识梳理
1.平行 2.相等 相等 3.距离 4.平分
5.相等 相等 平分 平行且相等 6.中点 7.平行于 等于
知识反馈
1.3? AEDE、 BDEF、?CDFE
4.D[解析]“∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AD∥BC
∴∠DAE=∠AEB.∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,
∴AB=BE.设AB=CD=x cm,则AD=BC=(x+2)cm,∵ ABCD的周长为20
cm,∴x+x+2=10,解得x=4,即AB=4cm,故选D.
5.(1)解:所有的全等三角形有:△ABF≌△CDE,△AED≌△CFB,△ADC≌△CBA
(2)证明:∵四边形ABCD是平行四边形,∴AB∥CD、且AB=CD.∴∠BAF=∠DCE.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.∴△ABF≌△CDE.∴∠AFB=∠CED.∴DE∥BF
6.D 8.C 9.21
10.证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,∠OAE∠OCF,
在△OAE和△OCF中,∠AOE=∠COF,OA=OC,∠OAE=∠OCF,∴△OAE≌△OCF(ASA),∴OE=OF
11.B 12.平行四边形 13.B
14.证明:∵四边形ABCD是平行四边形,∴∠DAB=∠BCD,∠B=∠D.∵AE平分
∠DAB,CF平分∠BCD,∴∠DAE=∠EAF=∠FCE=∠BCF.又∵∠AEC=∠DAE+∠D,∠AFC=∠BCF+∠B,∴∠AEC=∠AFC∴四边形AFCE是平行四边形.
15.证明:(1)∵AC∥BD,∴∠C=∠D.又∠COA=∠DOB,AO=BO,∴△AOC≌
△BOD(AAS).(2)∵△AOC≌△BOD.∴CO=DO.∵点E,F分别是OC,OD的中点,OF=OD,OE=OC,∴EO=FO又∵AO=BO,∴四边形AFBE是平行四边形
16.证明:在 ABCD中,AB∥DC,∴∠ABD=∠CDB.又FG⊥AB,EH⊥CD,
∴GF∥EH,∠BGF=∠DHE=900,在△BGF和△DHE中,BGF=∠DHE=900
∠ABD=∠CDB,BF=DE,∴△BGF≌△DHE(AAS).∴GB=HD.又GB∥DH,
∴四边形GBHD为平行四边形,∴GH与BD互相平分
17.A 18.C 19.2
20.证明:∵DE为△ABC的中位线,∴DE∥BC,DE=BC.即DF∥BC,2DE=EC,
又∵EF=DE,∴DF=BC.∴四边形BCFD为平行四边形.
A
E
F
D
A
A
D
C
D
B
E
C
B
B
C
A
F
E
C
A
D
B
a
A
C
F
B
G
D
E
b
D
A
C
B
第9题
第8题
O
B
A
C
D
O
C
B
D
A
O
E
D
A
F
C
B
A
E
C
D
D
F
C
B
B
A
C
D
O
F
E
B
A
E
C
D
F
B
A
O
F
E
D
A
B
D
D
A
A
E
D
E
O
C
B
C
B
A
D
E
F
C
B
知识梳理
两组对边分别 的四边形叫做平行四边形,平行四边形用“ ”
表示。
2.平行四边形的对边 ;平行四边形的对角 。
3.两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的 。
4.平行四边形的对角线互相 。
5.两组对边分别 的四边形是平行四边形;
两组对角分别 的四边形是平行四边形;
对角线互相 的四边形是平行四边形;
一组对边 的四边形是平行四边形。
6.连接三角形两边 的线段叫做三角形的中位线。
7.三角形的中位线 三角形的第三边,并且 第三边的一半。
知识反馈
★知识点1:平行四边形的概念
1.如图,点D,E,F分别在△ABC的三边BC,AC,AB上,且DE∥AB,DF∥AC,EF∥BC,则图中共有 个平行四边形,分别是 。
★知识点2:平行四边形的性质(边、角)
2.在 ABCD中,如果∠B=100°,那么∠A,∠D的度数分别是()
A.∠A=80°,∠D=100° B.∠A=100°,∠D=80°
C.∠A=80°,∠D=80° D.∠A=100°,∠D=100°
3.如图,在ABCD,AD=3cm,AB=2cm,则ABCD的周长等于( )
A.?10?cm B.?6?cm C.?5?cm D.?4?cm
第3题 第4题
4.如图, ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是
( )
A.10cm B.8cm C.6cm D.4cm
5.如图,在 ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,?BF
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF
★知识点3:两条平行线之间的距离
6.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G为垂足,则下列说法中错误的是
( )
AB=CD B.CE=FG
C.A,B两点的距离就是线段AB的长
D.直线a,b之间的距离就是线段CD的长
如图,四边形是平行四边.
(1)请在图中作出表示平行线AB与CD,AD与BC之间距离的线段;
(D)若AB=12,BC=20,S ABCD=20,求出所作线段的长度.
★知识点4平行四边形的性质(对角线)
8.如图, ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
AO=OD B.AO⊥OD? C.AO=OC D.AO⊥AB
9.如图,在 ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△OAB的周长为 .
10.如图,在 ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于点E,交CD于点F.求证:OE=OF
★知识点5:平行四边形的判定方法
11.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD B.BC=AD C.∠A=∠C D.BC∥AD
第11题 第12题
12.如图,△ABC中,DE∥BC,AE=EC,延长DE到F,使EF=DE,连接AF,FC,CD,则四边形ADCF是 .
13.如图,在 ABCD中,对角线AC与BD相交于点O,且E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
A.OE=OF
B.DE=BF
C.∠ADE=∠CBF
D.∠ABE=∠CDF
14.如图所示,在 ABCD中,AE,CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形.
如图所示,AB,CD相交于点O,AC∥DB,AO=BO.点E,F分别是OC,OD的中点.求证:
(1)△AOC≌△BOD
(2)四边形AFBE是平行四边形
如图,在 ABCD中,BF=DE,FG⊥AB于点G,EH⊥CD于点H,GH与BD交于点O.求证:GH与BD互相平分.
★知识点6:三角形的中位线及其定理
17.如图,D,E分别是△ABC的边AB,AC的中点,则△ABC的中位线是( )
A.线段DE B.线段CD C.线段BE D.以上答案都不对
第17题 第19题
18.已知△ABC的周长为40cm,中位线DE=6cm,EF=8cm,则另一条中位线DF的长是( )
A.4cm B.5cm C.6cm D.8cm
19.如图, ABCD的对角线AC,BD相交于点O,点E是CD的中点,若AD=4cm,则OE的长为 cm.
20.如图,已知DE为△ABC的中位线,延长DE到F,使EF=DE.
求证:四边形BCFD为平行四边形。
参 考 答 案
知识梳理
1.平行 2.相等 相等 3.距离 4.平分
5.相等 相等 平分 平行且相等 6.中点 7.平行于 等于
知识反馈
1.3? AEDE、 BDEF、?CDFE
4.D[解析]“∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,AD∥BC
∴∠DAE=∠AEB.∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,
∴AB=BE.设AB=CD=x cm,则AD=BC=(x+2)cm,∵ ABCD的周长为20
cm,∴x+x+2=10,解得x=4,即AB=4cm,故选D.
5.(1)解:所有的全等三角形有:△ABF≌△CDE,△AED≌△CFB,△ADC≌△CBA
(2)证明:∵四边形ABCD是平行四边形,∴AB∥CD、且AB=CD.∴∠BAF=∠DCE.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.∴△ABF≌△CDE.∴∠AFB=∠CED.∴DE∥BF
6.D 8.C 9.21
10.证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,∠OAE∠OCF,
在△OAE和△OCF中,∠AOE=∠COF,OA=OC,∠OAE=∠OCF,∴△OAE≌△OCF(ASA),∴OE=OF
11.B 12.平行四边形 13.B
14.证明:∵四边形ABCD是平行四边形,∴∠DAB=∠BCD,∠B=∠D.∵AE平分
∠DAB,CF平分∠BCD,∴∠DAE=∠EAF=∠FCE=∠BCF.又∵∠AEC=∠DAE+∠D,∠AFC=∠BCF+∠B,∴∠AEC=∠AFC∴四边形AFCE是平行四边形.
15.证明:(1)∵AC∥BD,∴∠C=∠D.又∠COA=∠DOB,AO=BO,∴△AOC≌
△BOD(AAS).(2)∵△AOC≌△BOD.∴CO=DO.∵点E,F分别是OC,OD的中点,OF=OD,OE=OC,∴EO=FO又∵AO=BO,∴四边形AFBE是平行四边形
16.证明:在 ABCD中,AB∥DC,∴∠ABD=∠CDB.又FG⊥AB,EH⊥CD,
∴GF∥EH,∠BGF=∠DHE=900,在△BGF和△DHE中,BGF=∠DHE=900
∠ABD=∠CDB,BF=DE,∴△BGF≌△DHE(AAS).∴GB=HD.又GB∥DH,
∴四边形GBHD为平行四边形,∴GH与BD互相平分
17.A 18.C 19.2
20.证明:∵DE为△ABC的中位线,∴DE∥BC,DE=BC.即DF∥BC,2DE=EC,
又∵EF=DE,∴DF=BC.∴四边形BCFD为平行四边形.
A
E
F
D
A
A
D
C
D
B
E
C
B
B
C
A
F
E
C
A
D
B
a
A
C
F
B
G
D
E
b
D
A
C
B
第9题
第8题
O
B
A
C
D
O
C
B
D
A
O
E
D
A
F
C
B
A
E
C
D
D
F
C
B
B
A
C
D
O
F
E
B
A
E
C
D
F
B
A
O
F
E
D
A
B
D
D
A
A
E
D
E
O
C
B
C
B
A
D
E
F
C
B
