【走进重高汇编】八下数学第十八章 正方形训练卷
文档属性
| 名称 | 【走进重高汇编】八下数学第十八章 正方形训练卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-04 21:34:37 | ||
图片预览



文档简介
八下数学走进重高汇编 第十八章 正方形
一.选择题(共10小题)
1.下列性质中,正方形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.四个角都是直角
2.正方形的面积是2,它的对角线长为( )
A.1 B.2 C. D.
3.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.45° B.35° C.22.5° D.15.5°
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选①③ C.选②④ D.选②③
5.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那么∠BEC等于( )
A.45° B.60° C.70° D.75°
6.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
7.如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A. B. C. D.
8.如图,在正方形ABCD中,E、F分别是边CD、AD上的点,且CE=DF.AE与BF相交于点O,则下列结论错误的是( )
A.AE=BF B.AE⊥BF C.AO=OE D.S△AOB=S四边形DEOF
9.如图,正方形ABCD中,点O为对角线AC的中点,矩形OMNP两边分别交AB、BC边于E、F两点,连结BO,下列结论:(1)图形中全等的三角形只有两对;(2)BE+BF=0A;(3)S四边形OEBF=S矩形OMNP;(4)AE2+FC2=EF2.正确的结论有( )个.
A.4个 B.3个 C.2个 D.1个
10.如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
A.7 B.8 C.9 D.14
二.填空题(共5小题)
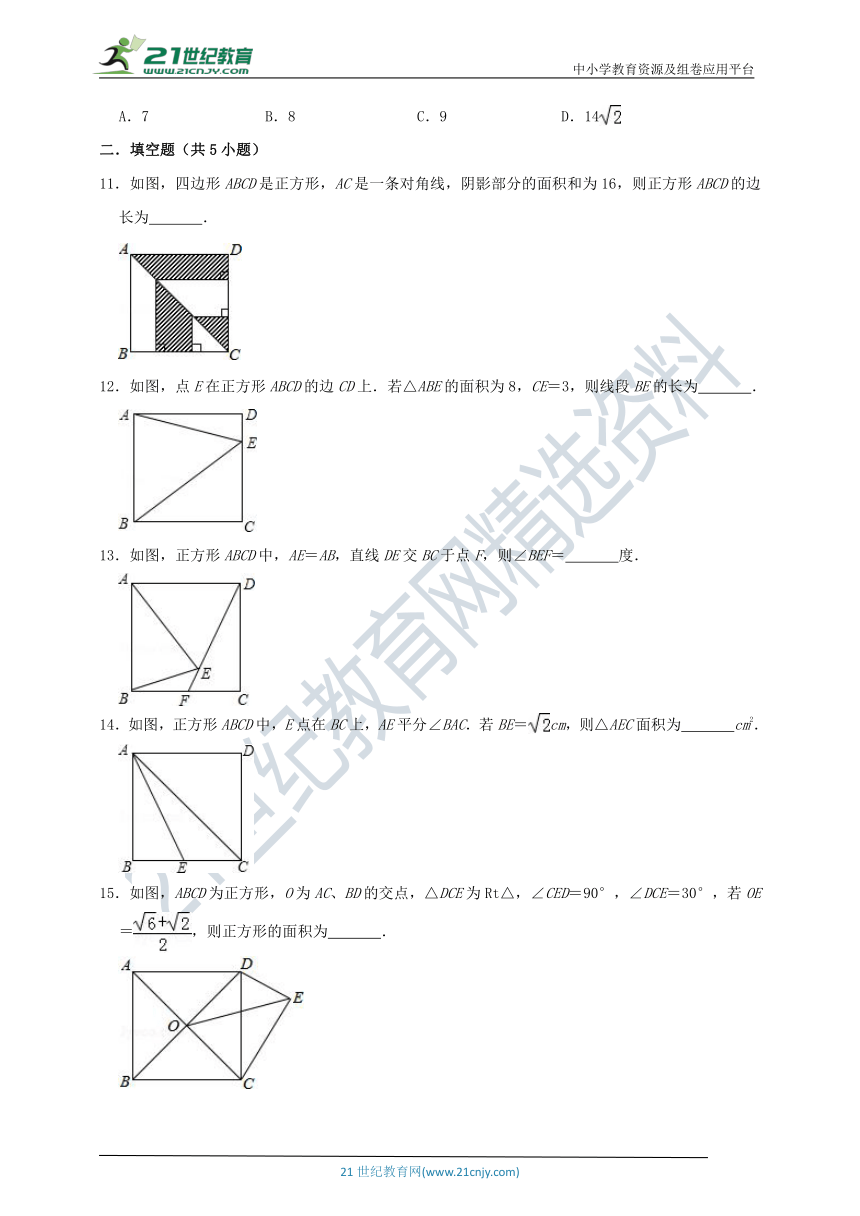
11.如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为 .
12.如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 .
13.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF= 度.
14.如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=cm,则△AEC面积为 cm2.
15.如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=,则正方形的面积为 .
三.解答题(共7小题)
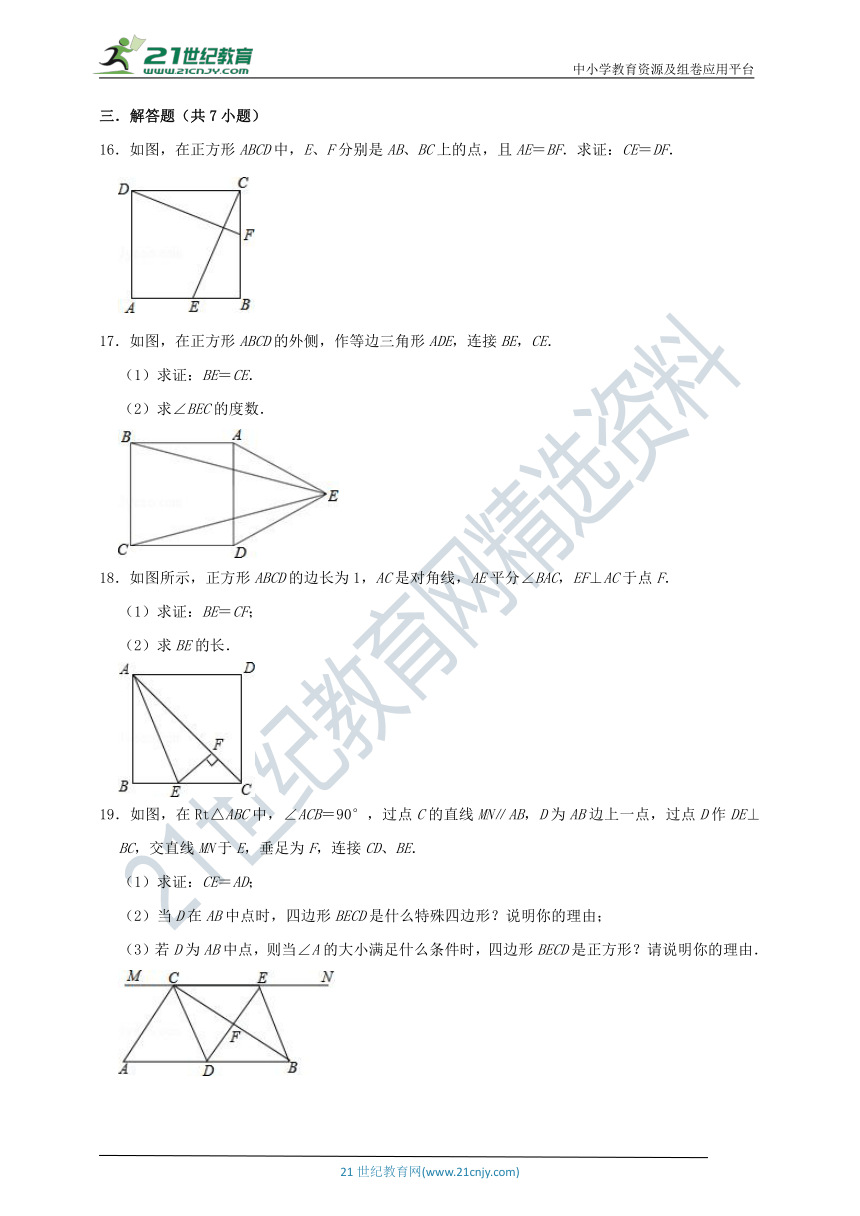
16.如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF.
17.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
18.如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
19.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
20.如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF.
(1)若DG=2,求证:四边形EFGH为正方形;
(2)若DG=6,求△FCG的面积.
21.已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
22.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为时,求正方形的边长.
八下数学走进重高汇编 第十八章 正方形
参考答案与试题解析
一.选择题(共10小题)
1.下列性质中,正方形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.四个角都是直角
【解答】解:A、正方形的对角线互相垂直平分,矩形的对角线互相平分但不一定垂直,故本选项正确.
B、正方形和矩形的对角线都互相平分,故本选项错误;
C、正方形和矩形的对角线都相等,故本选项错误;
D、正方形和矩形的四个角都是直角,故本选项错误;
故选:A.
2.正方形的面积是2,它的对角线长为( )
A.1 B.2 C. D.
【解答】解:如图所示:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴正方形的面积=AC?BD=AC2=2,
∴AC2=4,
∴AC=2,
故选:B.
3.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.45° B.35° C.22.5° D.15.5°
【解答】解:∵四边形ABCD是正方形,
∴∠CAB=∠BCA=45°;
△ACE中,AC=AE,则:
∠ACE=∠AEC=(180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
故选:C.
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选①③ C.选②④ D.选②③
【解答】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
C、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,
所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意.
故选:D.
5.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那么∠BEC等于( )
A.45° B.60° C.70° D.75°
【解答】解:∵AD=CD,∠ADE=∠CDE,DE=DE
∴△AED≌△CED
∴∠ECF=∠DAF=25°,
又∵在△DEC中,∠CDE=45°,
∴∠CED=180°﹣25°﹣45°=110°,
∴∠BEC=180°﹣110°=70°.
故选:C.
6.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
【解答】解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH==,
∴四边形EFGH的面积是:×=34,
故选:B.
7.如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A. B. C. D.
【解答】解:∵四边形ABCD是正方形,
∴AB=AD=1,AC⊥BD,∠ABC=∠BCD=90°,∠CBO=∠BCO=45°,OB=BD,
∴BD==,∠BOC=90°,
∴OB=,
∵PE⊥BD于点E,PF⊥AC于点F,
∴∠OEP=∠OFP=90°=∠EOF,△BEP是等腰直角三角形,
∴四边形OEPF是矩形,PE=BE,
∴PF=OE,
∴PE+PF=BE+OE=OB=;
故选:B.
8.如图,在正方形ABCD中,E、F分别是边CD、AD上的点,且CE=DF.AE与BF相交于点O,则下列结论错误的是( )
A.AE=BF B.AE⊥BF
C.AO=OE D.S△AOB=S四边形DEOF
【解答】解:A、∵在正方形ABCD中,
∴AB=BC=CD=AD,
又∵CE=DF,
∴AF=DE,
∵∠D=∠BAF=90°,
∴△BAF≌△ADE,
∴AE=BF,
故此选项正确;
B、∵△BAF≌△ADE,
∴∠BFA=∠AED,
∵∠AED+∠EAD=90°,
∴∠BFA+∠EAD=90°,
∴∠AOF=90°,
∴AE⊥BF,
故此选项正确;
C、如图,连接BE,
假设AO=OE,
∵BF⊥AE,
∴∠AOB=∠BOE=90°,
∵BO=BO,
∴△ABO≌△EBO,
∴AB=BE,
又∵AB=BC,
BC<BE,
∴AB不可能等于BE,
∴假设AO=OE,不成立,即AO≠OE,
故此选项错误;
D、∵△BAF≌△ADE,
∴S△BAF=S△ADE,
∴S△BAF﹣S△AOF=S△ADE﹣S△AOF,
∴S△AOB=S四边形DEOF,故此选项正确.
故选:C.
9.如图,正方形ABCD中,点O为对角线AC的中点,矩形OMNP两边分别交AB、BC边于E、F两点,连结BO,下列结论:( )
(1)图形中全等的三角形只有两对;(2)BE+BF=0A;(3)S四边形OEBF=S矩形OMNP;(4)AE2+FC2=EF2.
正确的结论有( )个.
A.4个 B.3个 C.2个 D.1个
【解答】解:(1)错误.△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;
(2)正确.BE+BF=AB=OA;
(3)错误.∵△AOE≌△BOF,∴四边形BEOF的面积=△ABO的面积=正方形ABCD的面积;
(4)正确.
AE2+CF2=BE2+BF2=EF2.
故选:C.
10.如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
A.7 B.8 C.9 D.14
【解答】解:如图,
延长AB、DC交于M点,延长CD、FE交于N点,延长EF、HG交于P点,延长GH、BA交于Q点,则MNPQ是矩形,
∵∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=135°,
∴△BCM、△DEN、△FGP、△AHQ均为等腰直角三角形.
这个八边形的面积等于=矩形面积﹣4个小三角形的面积=3×3﹣4×1×1÷2=7.
故选:A.
二.填空题(共5小题)
11.如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为 4 .
【解答】解:∵四边形ABCD是正方形,AC是对角线,
∴AB=BC=CD=DA,阴影部分的面积和=正方形ABCD的面积,
∵阴影部分的面积和为16,
即AB2=16,
∴AB2=32,
∴AB==4;
故答案为:4.
12.如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 5 .
【解答】解:
过E作EM⊥AB于M,
∵四边形ABCD是正方形,
∴AD=BC=CD=AB,
∴EM=AD,BM=CE,
∵△ABE的面积为8,
∴×AB×EM=8,
解得:EM=4,
即AD=DC=BC=AB=4,
∵CE=3,
由勾股定理得:BE===5,
故答案为:5.
13.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF= 45 度.
【解答】解:设∠BAE=x°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵AE=AB,
∴AB=AE=AD,
∴∠ABE=∠AEB=(180°﹣∠BAE)=90°﹣x°,
∠DAE=90°﹣x°,
∠AED=∠ADE=(180°﹣∠DAE)=[180°﹣(90°﹣x°)]=45°+x°,
∴∠BEF=180°﹣∠AEB﹣∠AED
=180°﹣(90°﹣x°)﹣(45°+x°)
=45°.
答:∠BEF的度数是45°.
故答案为:45.
14.如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=cm,则△AEC面积为 cm2.
【解答】解:设正方形的边长为a,
∵AE平分∠BAC,
∴tan∠ABC=tan2∠BAE,
解得a=2+,
由△AEC面积=△ABC面积﹣△ABE的面积=(2+)(2)﹣(2)=2+.
故答案为:2+.
15.如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=,则正方形的面积为 4 .
【解答】解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
∵,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
设正方形ABCD的边长为2a,则OC=OD=×2a=a,
∵∠CED=90°,∠DCE=30°,
∴CD=2a,DE=a,
由勾股定理得,得,
∵OE=,
∴四边形OCED的面积=
四边形OMEN的面积=,
∵四边形OCED的面积=四边形OMEN的面积,即可得:=,
解得a2=1,
∴正方形ABCD的面积=(2a)2=4a2=4×1=4,
故答案为:4
三.解答题(共7小题)
16.如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF.
【解答】证明:在正方形ABCD中,AB=BC=CD,∠B=∠BCD=90°,
∵AE=BF,
∴AB﹣AE=BC﹣BF,
即BE=CF,
在△BCE和△CDF中,
,
∴△BCE≌△CDF(SAS),
∴CE=DF.
17.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
【解答】( 1)证明:∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°,
∵三角形ADE为正三角形,
∴AE=AD=DE,∠EAD=∠EDA=60°,
∴∠BAE=∠CDE=150°,
在△BAE和△CDE中
,
∴△BAE≌△CDE(SAS),
∴BE=CE;
(2)解:∵AB=AD,AD=AE,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAE=150°,
∴∠ABE=∠AEB=15°,
同理:∠CED=15°
∴∠BEC=60°﹣15°×2=30°.
18.如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
【解答】(1)证明:∵四边形ABCD为正方形,
∴∠B=90°,
∵EF⊥AC,
∴∠EFA=90°,
∵AE平分∠BAC,
∴BE=EF,
又∵AC平分∠BCD,
∴∠ACB=45°,
∴∠FEC=∠FCE,
∴EF=FC,
∴BE=CF;
(2)解:设BE=x,则EF=CF=x,
在Rt△CEF中可求得CE=x,
∵BC=1,
∴x+x=1,解得x=﹣1,
即BE的长为﹣1.
19.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
【解答】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴?四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
20.如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF.
(1)若DG=2,求证:四边形EFGH为正方形;
(2)若DG=6,求△FCG的面积.
【解答】(1)证明:∵四边形EFGH为菱形,
∴HG=EH,
∵AH=2,DG=2,
∴DG=AH,
在Rt△DHG和△AEH中,
,
∴Rt△DHG≌△AEH,
∴∠DHG=∠AHE,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∵四边形EFGH为菱形,
∴四边形EFGH为正方形;
(2)解:作FQ⊥CD于Q,连结GE,如图,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠AEG=∠QGE,即∠AEH+∠HEG=∠QGF+∠FGE,
∵四边形EFGH为菱形,
∴HE=GF,HE∥GF,
∴∠HEG=∠FGE,
∴∠AEH=∠QGF,
在△AEH和△QGF中
,
∴△AEH≌△QGF,
∴AH=QF=2,
∵DG=6,CD=8,
∴CG=2,
∴△FCG的面积=CG?FQ=×2×2=2.
21.已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
【解答】(1)证明:连接BG和CE交于O,
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AC=AG,∠EAB=∠GAC,
∴∠EAB+∠EAG=∠GAC+∠EAG,
∴∠GAB=∠EAC,
在△BAG和△EAC中,
,
∴△BAG≌△EAC(SAS),
∴BG=CE.
(2)四边形PQMN为正方形,
证明:∵EB、BC、CG、GE的中点分别是P、Q、M、N,
∴PN∥BG,MN=CE,MN∥CE,PQ=CE,PQ∥CE,PN=BG,
∵BG=CE,
∴PN=MN,MN=PQ,MN∥PQ,
∴四边形PQMN是菱形,
∵△BAG≌△EAC,
∴∠GBA=∠AEC,
∵四边形ABDE是正方形,
∴∠EAB=90°,
∴∠ABG+∠BWA=90°,
∵∠BWA=∠GWE,
∴∠GWE+∠AEC=90°,
∴∠EOW=180°﹣90°=90°,
∵MN∥CE,PN∥BG,
∴∠NZO=∠EOW=90°,∠NIO=90°,
∴∠MNP=360°﹣90°﹣90°﹣90°=90°
∴菱形PQMN是正方形,
即四边形PQMN为正方形.
22.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为时,求正方形的边长.
【解答】(1)证明:∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN﹣∠ABN=∠ABE﹣∠ABN.
即∠MBA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
(2)解:①当M点落在BD的中点时,A、M、C三点共线,AM+CM的值最小.②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小.
理由如下:连接MN,由(1)知,△AMB≌△ENB,
∴AM=EN,
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”可知,若E、N、M、C在同一条直线上时,EN+MN+CM取得最小值,最小值为EC.
在△ABM和△CBM中,
,∴△ABM≌△CBM,∴∠BAM=∠BCM,∴∠BCM=∠BEN,∵EB=CB,
∴若连接EC,则∠BEC=∠BCE,
∵∠BCM=∠BCE,∠BEN=∠BEC,∴M、N可以同时在直线EC上.
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
(3)解:过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=∠ABF﹣∠ABE=90°﹣60°=30°.
设正方形的边长为x,则BF=x,EF=.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴()2+(x+x)2=.
解得x1=,x2=﹣(舍去负值).
∴正方形的边长为.
一.选择题(共10小题)
1.下列性质中,正方形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.四个角都是直角
2.正方形的面积是2,它的对角线长为( )
A.1 B.2 C. D.
3.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.45° B.35° C.22.5° D.15.5°
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选①③ C.选②④ D.选②③
5.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那么∠BEC等于( )
A.45° B.60° C.70° D.75°
6.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
7.如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A. B. C. D.
8.如图,在正方形ABCD中,E、F分别是边CD、AD上的点,且CE=DF.AE与BF相交于点O,则下列结论错误的是( )
A.AE=BF B.AE⊥BF C.AO=OE D.S△AOB=S四边形DEOF
9.如图,正方形ABCD中,点O为对角线AC的中点,矩形OMNP两边分别交AB、BC边于E、F两点,连结BO,下列结论:(1)图形中全等的三角形只有两对;(2)BE+BF=0A;(3)S四边形OEBF=S矩形OMNP;(4)AE2+FC2=EF2.正确的结论有( )个.
A.4个 B.3个 C.2个 D.1个
10.如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
A.7 B.8 C.9 D.14
二.填空题(共5小题)
11.如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为 .
12.如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 .
13.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF= 度.
14.如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=cm,则△AEC面积为 cm2.
15.如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=,则正方形的面积为 .
三.解答题(共7小题)
16.如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF.
17.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
18.如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
19.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
20.如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF.
(1)若DG=2,求证:四边形EFGH为正方形;
(2)若DG=6,求△FCG的面积.
21.已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
22.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为时,求正方形的边长.
八下数学走进重高汇编 第十八章 正方形
参考答案与试题解析
一.选择题(共10小题)
1.下列性质中,正方形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.四个角都是直角
【解答】解:A、正方形的对角线互相垂直平分,矩形的对角线互相平分但不一定垂直,故本选项正确.
B、正方形和矩形的对角线都互相平分,故本选项错误;
C、正方形和矩形的对角线都相等,故本选项错误;
D、正方形和矩形的四个角都是直角,故本选项错误;
故选:A.
2.正方形的面积是2,它的对角线长为( )
A.1 B.2 C. D.
【解答】解:如图所示:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴正方形的面积=AC?BD=AC2=2,
∴AC2=4,
∴AC=2,
故选:B.
3.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
A.45° B.35° C.22.5° D.15.5°
【解答】解:∵四边形ABCD是正方形,
∴∠CAB=∠BCA=45°;
△ACE中,AC=AE,则:
∠ACE=∠AEC=(180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
故选:C.
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选①③ C.选②④ D.选②③
【解答】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
C、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,
所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意.
故选:D.
5.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那么∠BEC等于( )
A.45° B.60° C.70° D.75°
【解答】解:∵AD=CD,∠ADE=∠CDE,DE=DE
∴△AED≌△CED
∴∠ECF=∠DAF=25°,
又∵在△DEC中,∠CDE=45°,
∴∠CED=180°﹣25°﹣45°=110°,
∴∠BEC=180°﹣110°=70°.
故选:C.
6.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
【解答】解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH==,
∴四边形EFGH的面积是:×=34,
故选:B.
7.如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A. B. C. D.
【解答】解:∵四边形ABCD是正方形,
∴AB=AD=1,AC⊥BD,∠ABC=∠BCD=90°,∠CBO=∠BCO=45°,OB=BD,
∴BD==,∠BOC=90°,
∴OB=,
∵PE⊥BD于点E,PF⊥AC于点F,
∴∠OEP=∠OFP=90°=∠EOF,△BEP是等腰直角三角形,
∴四边形OEPF是矩形,PE=BE,
∴PF=OE,
∴PE+PF=BE+OE=OB=;
故选:B.
8.如图,在正方形ABCD中,E、F分别是边CD、AD上的点,且CE=DF.AE与BF相交于点O,则下列结论错误的是( )
A.AE=BF B.AE⊥BF
C.AO=OE D.S△AOB=S四边形DEOF
【解答】解:A、∵在正方形ABCD中,
∴AB=BC=CD=AD,
又∵CE=DF,
∴AF=DE,
∵∠D=∠BAF=90°,
∴△BAF≌△ADE,
∴AE=BF,
故此选项正确;
B、∵△BAF≌△ADE,
∴∠BFA=∠AED,
∵∠AED+∠EAD=90°,
∴∠BFA+∠EAD=90°,
∴∠AOF=90°,
∴AE⊥BF,
故此选项正确;
C、如图,连接BE,
假设AO=OE,
∵BF⊥AE,
∴∠AOB=∠BOE=90°,
∵BO=BO,
∴△ABO≌△EBO,
∴AB=BE,
又∵AB=BC,
BC<BE,
∴AB不可能等于BE,
∴假设AO=OE,不成立,即AO≠OE,
故此选项错误;
D、∵△BAF≌△ADE,
∴S△BAF=S△ADE,
∴S△BAF﹣S△AOF=S△ADE﹣S△AOF,
∴S△AOB=S四边形DEOF,故此选项正确.
故选:C.
9.如图,正方形ABCD中,点O为对角线AC的中点,矩形OMNP两边分别交AB、BC边于E、F两点,连结BO,下列结论:( )
(1)图形中全等的三角形只有两对;(2)BE+BF=0A;(3)S四边形OEBF=S矩形OMNP;(4)AE2+FC2=EF2.
正确的结论有( )个.
A.4个 B.3个 C.2个 D.1个
【解答】解:(1)错误.△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;
(2)正确.BE+BF=AB=OA;
(3)错误.∵△AOE≌△BOF,∴四边形BEOF的面积=△ABO的面积=正方形ABCD的面积;
(4)正确.
AE2+CF2=BE2+BF2=EF2.
故选:C.
10.如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
A.7 B.8 C.9 D.14
【解答】解:如图,
延长AB、DC交于M点,延长CD、FE交于N点,延长EF、HG交于P点,延长GH、BA交于Q点,则MNPQ是矩形,
∵∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=135°,
∴△BCM、△DEN、△FGP、△AHQ均为等腰直角三角形.
这个八边形的面积等于=矩形面积﹣4个小三角形的面积=3×3﹣4×1×1÷2=7.
故选:A.
二.填空题(共5小题)
11.如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为 4 .
【解答】解:∵四边形ABCD是正方形,AC是对角线,
∴AB=BC=CD=DA,阴影部分的面积和=正方形ABCD的面积,
∵阴影部分的面积和为16,
即AB2=16,
∴AB2=32,
∴AB==4;
故答案为:4.
12.如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 5 .
【解答】解:
过E作EM⊥AB于M,
∵四边形ABCD是正方形,
∴AD=BC=CD=AB,
∴EM=AD,BM=CE,
∵△ABE的面积为8,
∴×AB×EM=8,
解得:EM=4,
即AD=DC=BC=AB=4,
∵CE=3,
由勾股定理得:BE===5,
故答案为:5.
13.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF= 45 度.
【解答】解:设∠BAE=x°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵AE=AB,
∴AB=AE=AD,
∴∠ABE=∠AEB=(180°﹣∠BAE)=90°﹣x°,
∠DAE=90°﹣x°,
∠AED=∠ADE=(180°﹣∠DAE)=[180°﹣(90°﹣x°)]=45°+x°,
∴∠BEF=180°﹣∠AEB﹣∠AED
=180°﹣(90°﹣x°)﹣(45°+x°)
=45°.
答:∠BEF的度数是45°.
故答案为:45.
14.如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=cm,则△AEC面积为 cm2.
【解答】解:设正方形的边长为a,
∵AE平分∠BAC,
∴tan∠ABC=tan2∠BAE,
解得a=2+,
由△AEC面积=△ABC面积﹣△ABE的面积=(2+)(2)﹣(2)=2+.
故答案为:2+.
15.如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=,则正方形的面积为 4 .
【解答】解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
∵,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
设正方形ABCD的边长为2a,则OC=OD=×2a=a,
∵∠CED=90°,∠DCE=30°,
∴CD=2a,DE=a,
由勾股定理得,得,
∵OE=,
∴四边形OCED的面积=
四边形OMEN的面积=,
∵四边形OCED的面积=四边形OMEN的面积,即可得:=,
解得a2=1,
∴正方形ABCD的面积=(2a)2=4a2=4×1=4,
故答案为:4
三.解答题(共7小题)
16.如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF.
【解答】证明:在正方形ABCD中,AB=BC=CD,∠B=∠BCD=90°,
∵AE=BF,
∴AB﹣AE=BC﹣BF,
即BE=CF,
在△BCE和△CDF中,
,
∴△BCE≌△CDF(SAS),
∴CE=DF.
17.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
【解答】( 1)证明:∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°,
∵三角形ADE为正三角形,
∴AE=AD=DE,∠EAD=∠EDA=60°,
∴∠BAE=∠CDE=150°,
在△BAE和△CDE中
,
∴△BAE≌△CDE(SAS),
∴BE=CE;
(2)解:∵AB=AD,AD=AE,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAE=150°,
∴∠ABE=∠AEB=15°,
同理:∠CED=15°
∴∠BEC=60°﹣15°×2=30°.
18.如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
【解答】(1)证明:∵四边形ABCD为正方形,
∴∠B=90°,
∵EF⊥AC,
∴∠EFA=90°,
∵AE平分∠BAC,
∴BE=EF,
又∵AC平分∠BCD,
∴∠ACB=45°,
∴∠FEC=∠FCE,
∴EF=FC,
∴BE=CF;
(2)解:设BE=x,则EF=CF=x,
在Rt△CEF中可求得CE=x,
∵BC=1,
∴x+x=1,解得x=﹣1,
即BE的长为﹣1.
19.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
【解答】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴?四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
20.如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF.
(1)若DG=2,求证:四边形EFGH为正方形;
(2)若DG=6,求△FCG的面积.
【解答】(1)证明:∵四边形EFGH为菱形,
∴HG=EH,
∵AH=2,DG=2,
∴DG=AH,
在Rt△DHG和△AEH中,
,
∴Rt△DHG≌△AEH,
∴∠DHG=∠AHE,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∵四边形EFGH为菱形,
∴四边形EFGH为正方形;
(2)解:作FQ⊥CD于Q,连结GE,如图,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠AEG=∠QGE,即∠AEH+∠HEG=∠QGF+∠FGE,
∵四边形EFGH为菱形,
∴HE=GF,HE∥GF,
∴∠HEG=∠FGE,
∴∠AEH=∠QGF,
在△AEH和△QGF中
,
∴△AEH≌△QGF,
∴AH=QF=2,
∵DG=6,CD=8,
∴CG=2,
∴△FCG的面积=CG?FQ=×2×2=2.
21.已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.
(1)若连接BG、CE,求证:BG=CE.
(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.
【解答】(1)证明:连接BG和CE交于O,
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AC=AG,∠EAB=∠GAC,
∴∠EAB+∠EAG=∠GAC+∠EAG,
∴∠GAB=∠EAC,
在△BAG和△EAC中,
,
∴△BAG≌△EAC(SAS),
∴BG=CE.
(2)四边形PQMN为正方形,
证明:∵EB、BC、CG、GE的中点分别是P、Q、M、N,
∴PN∥BG,MN=CE,MN∥CE,PQ=CE,PQ∥CE,PN=BG,
∵BG=CE,
∴PN=MN,MN=PQ,MN∥PQ,
∴四边形PQMN是菱形,
∵△BAG≌△EAC,
∴∠GBA=∠AEC,
∵四边形ABDE是正方形,
∴∠EAB=90°,
∴∠ABG+∠BWA=90°,
∵∠BWA=∠GWE,
∴∠GWE+∠AEC=90°,
∴∠EOW=180°﹣90°=90°,
∵MN∥CE,PN∥BG,
∴∠NZO=∠EOW=90°,∠NIO=90°,
∴∠MNP=360°﹣90°﹣90°﹣90°=90°
∴菱形PQMN是正方形,
即四边形PQMN为正方形.
22.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为时,求正方形的边长.
【解答】(1)证明:∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN﹣∠ABN=∠ABE﹣∠ABN.
即∠MBA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
(2)解:①当M点落在BD的中点时,A、M、C三点共线,AM+CM的值最小.②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小.
理由如下:连接MN,由(1)知,△AMB≌△ENB,
∴AM=EN,
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”可知,若E、N、M、C在同一条直线上时,EN+MN+CM取得最小值,最小值为EC.
在△ABM和△CBM中,
,∴△ABM≌△CBM,∴∠BAM=∠BCM,∴∠BCM=∠BEN,∵EB=CB,
∴若连接EC,则∠BEC=∠BCE,
∵∠BCM=∠BCE,∠BEN=∠BEC,∴M、N可以同时在直线EC上.
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
(3)解:过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=∠ABF﹣∠ABE=90°﹣60°=30°.
设正方形的边长为x,则BF=x,EF=.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴()2+(x+x)2=.
解得x1=,x2=﹣(舍去负值).
∴正方形的边长为.
