18.1 平行四边形的性质与判定培优提高试题(含解析)
文档属性
| 名称 | 18.1 平行四边形的性质与判定培优提高试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-04 00:00:00 | ||
图片预览



文档简介
八下数学培优提高 第十八章 平行四边形的性质与判定
一.选择题(共10小题)
1.?ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )
A.∠A=100°,∠D=80° B.∠A=80°,∠D=100°
C.∠B=80°,∠D=80° D.∠A=100°,∠D=100°
2.如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )
A.2:1 B.3:1 C.3:2 D.4:3
3.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AB=CD
C.AB∥CD,AD∥BC D.AB=CD,AD∥BC
4.如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
A.10cm B.8cm C.6cm D.4cm
5.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
A.1种 B.2种 C.3种 D.无数种
6.如图,已知在四边形ABCD中,AB∥CD,AB=CD,E为AB上一点,过点E作EF∥BC,交CD于点F,G为AD上一点,H为BC上一点,连接CG,AH.若GD=BH,则图中的平行四边形有( )
A.2个 B.3个 C.4个 D.6个
7.已知平行四边形一边长为8,一条对角线长为6,则另一条对角线α满足( )
A.10<α<22 B.4<α<20 C.4<α<28 D.2<α<14
8.在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别是(0,0)、(3,0)、(4,2),则顶点D的坐标为( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
9.如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4 B.3 C.2 D.
10.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;
⑤∠APB的大小.其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
二.填空题(共11小题)
11.在?ABCD中,AB=6cm,BC=8cm,则?ABCD的周长为 cm.
12.如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
13.如图,四边形ABCD中,对角线BD⊥AD,BD⊥BC,AD=11﹣x,BC=x﹣5,则当x= 时,四边形ABCD是平行四边形.
14.如图,F、G、H分别是平行四边形ABCD的边BC、CD、AD上的三等分点,E是AB边的中点,已知四边形EFGH的面积是51平方厘米,那么平行四边形ABCD的面积是 平方厘米.
15.如图,在?ABCD中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为 .
16.如图,?ABCD中,AD=10,AD边上的高为8,对角线交点为O,直线EF经过O,与AB、CD分别交于点E、F;直线GH经过点O,与AD、BC分别交于点G、H;直线MN经过点O,与AD、BC分别交于点M、N,则图中阴影部分的面积为 .
17.如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 .
18.已知a、b、c、d为四边形的四边长,a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是 四边形.
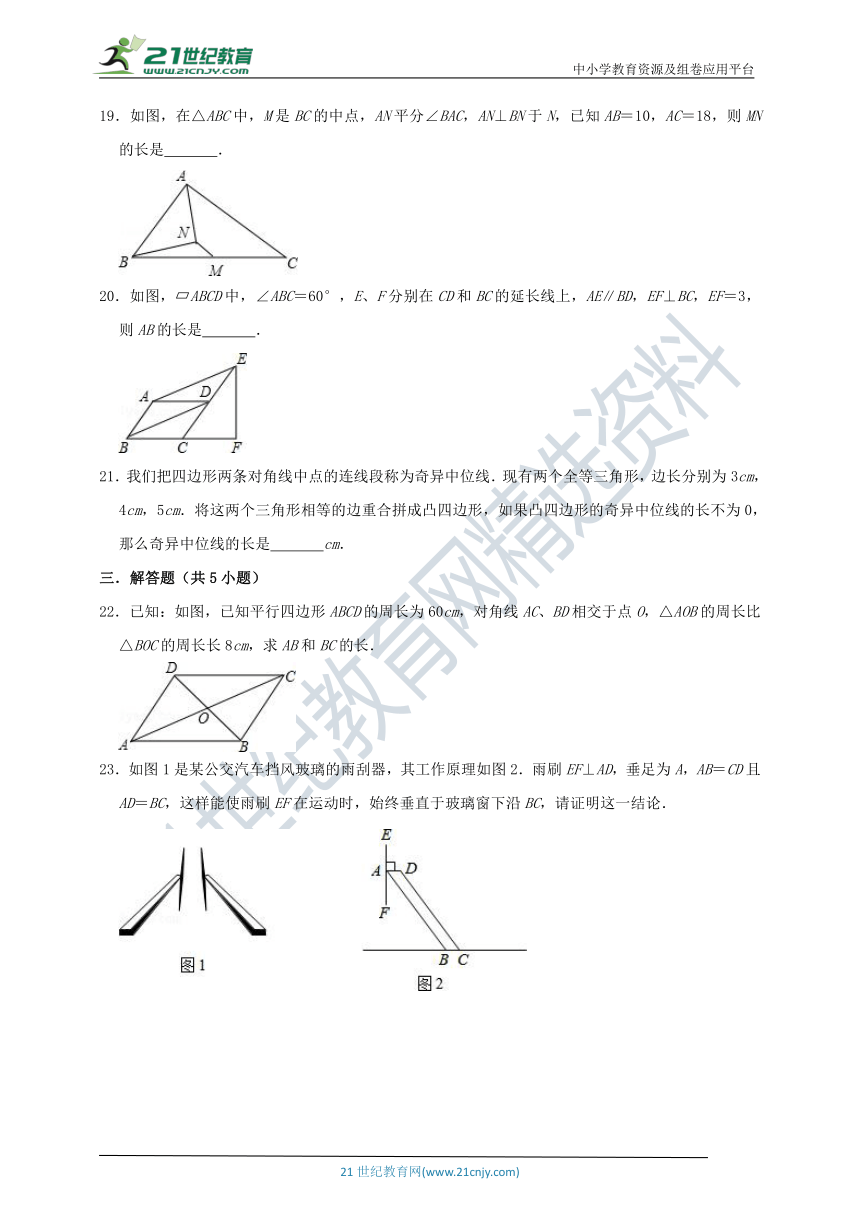
19.如图,在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN于N,已知AB=10,AC=18,则MN的长是 .
20.如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是 .
21.我们把四边形两条对角线中点的连线段称为奇异中位线.现有两个全等三角形,边长分别为3cm,4cm,5cm.将这两个三角形相等的边重合拼成凸四边形,如果凸四边形的奇异中位线的长不为0,那么奇异中位线的长是 cm.
三.解答题(共5小题)
22.已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
23.如图1是某公交汽车挡风玻璃的雨刮器,其工作原理如图2.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
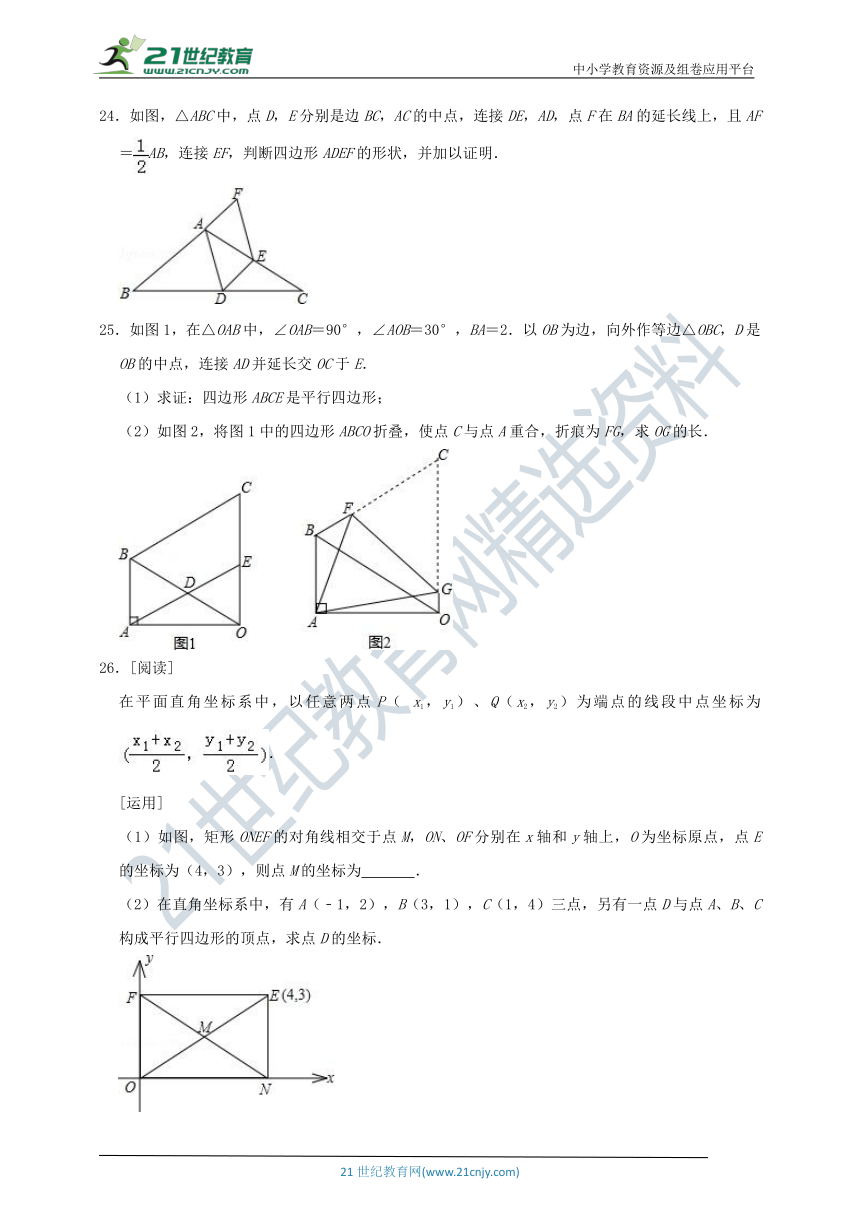
24.如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF,判断四边形ADEF的形状,并加以证明.
25.如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
26.[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为.
[运用]
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
八下数学培优提高 第十八章 平行四边形的性质与判定
参考答案与试题解析
一.选择题(共10小题)
1.?ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )
A.∠A=100°,∠D=80° B.∠A=80°,∠D=100°
C.∠B=80°,∠D=80° D.∠A=100°,∠D=100°
【解答】解:∵∠A与∠B是邻角,
∴∠A=180°﹣∠B=80°,
∴∠D=∠B=100°
故选:B.
2.如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )
A.2:1 B.3:1 C.3:2 D.4:3
【解答】解:过E作EM∥AB与GC交于点M,
∴△EMF≌△DGF,
∴EM=GD,
∵DE是中位线,
∴CE=AC,
又∵EM∥AG,
∴EM:AG=CE:AC=1:2,
又∵EM=GD,
∴AG:GD=2:1.
故选:A.
3.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AB=CD
C.AB∥CD,AD∥BC D.AB=CD,AD∥BC
【解答】解:A、∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
故A可以判断四边形ABCD是平行四边形.
B、∵AB∥CD,AB=CD,
∴∴四边形ABCD是平行四边形,
故B可以判断四边形ABCD是平行四边形.
C、∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
故C可以判断四边形ABCD是平行四边形.
D、∵AB=CD,AD∥BC,
∴四边形ABCD可能是平行四边形,有可能是等腰梯形.
故D不可以判断四边形ABCD是平行四边形.
故选:D.
4.如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
A.10cm B.8cm C.6cm D.4cm
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠DAE=∠BAE,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
设AB=CD=xcm,则AD=BC=(x+2)cm,
∵?ABCD的周长为20cm,
∴x+x+2=10,
解得:x=4,
即AB=4cm,
故选:D.
5.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
A.1种 B.2种 C.3种 D.无数种
【解答】解:因为平行四边形是中心对称图形,任意一条过平行四边形对角线交点的直线都平分四边形的面积,则这样的折纸方法共有无数种.
故选:D.
6.如图,已知在四边形ABCD中,AB∥CD,AB=CD,E为AB上一点,过点E作EF∥BC,交CD于点F,G为AD上一点,H为BC上一点,连接CG,AH.若GD=BH,则图中的平行四边形有( )
A.2个 B.3个 C.4个 D.6个
【解答】解:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
又∵EF∥BC,
∴四边形AEFD、四边形BCFE均为平行四边形,
∵GD=BH,AD=BC,
∴AG=CH,
又∵AG∥CH,
∴四边形AHCG是平行四边形,
又∵EF∥BC,
∴四边形AMNG、四边形MNCH均为平行四边形,
∴共有6个平行四边形,
故选:D.
7.已知平行四边形一边长为8,一条对角线长为6,则另一条对角线α满足( )
A.10<α<22 B.4<α<20 C.4<α<28 D.2<α<14
【解答】解:如图,已知平行四边形中,AB=8,AC=6,求BD的取值范围,即α的取值范围.
∵四边形ABCD是平行四边形,
∴α=2OB,AC=2OA=6,
∴OB=α,OA=3,
∴在△AOB中:AB﹣OA<OB<AB+OA
即:10<α<22,
故选:A.
8.在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别是(0,0)、(3,0)、(4,2),则顶点D的坐标为( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
【解答】解:如图:
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∵?ABCD的顶点A、B、C的坐标分别是(0,0)、(3,0)、(4,2),
∴顶点D的坐标为(1,2).
故选:C.
9.如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4 B.3 C.2 D.
【解答】解:∵四边形ABCD是菱形,
∴BC=CD,∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴BC×AE=CD×AF,∠BAE=∠DAF=30°,
∴AE=AF,
∵∠B=60°,
∴∠BAD=120°,
∴∠EAF=120°﹣30°﹣30°=60°,
∴△AEF是等边三角形,
∴AE=EF,∠AEF=60°,
∵AB=4,
∴BE=2,
∴AE==2,
∴EF=AE=2,
过A作AM⊥EF,
∴AM=AE?sin60°=3,
∴△AEF的面积是:EF?AM=×2×3=3.
故选:B.
10.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
【解答】解:∵点A,B为定点,点M,N分别为PA,PB的中点,
∴MN是△PAB的中位线,
∴MN=AB,
即线段MN的长度不变,故①错误;
PA、PB的长度随点P的移动而变化,
所以,△PAB的周长会随点P的移动而变化,故②正确;
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变,故③错误;
直线MN,AB之间的距离不随点P的移动而变化,故④错误;
∠APB的大小点P的移动而变化,故⑤正确.
综上所述,会随点P的移动而变化的是②⑤.
故选:B.
二.填空题(共11小题)
11.在?ABCD中,AB=6cm,BC=8cm,则?ABCD的周长为 28 cm.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD=6,BC=AD=8,
∴平行四边形ABCD的周长是AB+BC+CD+AD=6+8+6+8=28cm.
故答案为:28.
12.如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 50° .
【解答】解:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠C=∠ABF.
又∵∠C=40°,
∴∠ABF=40°.
∵EF⊥BF,
∴∠F=90°,
∴∠BEF=90°﹣40°=50°.
故答案是:50°.
13.如图,四边形ABCD中,对角线BD⊥AD,BD⊥BC,AD=11﹣x,BC=x﹣5,则当x= 8 时,四边形ABCD是平行四边形.
【解答】解:∵BD⊥AD,BD⊥BC,
∴AD∥BC,
只要AD=BC,四边形ABCD是平行四边形.
AD=BC
11﹣x=x﹣5
x=8.
故答案为:8.
14.如图,F、G、H分别是平行四边形ABCD的边BC、CD、AD上的三等分点,E是AB边的中点,已知四边形EFGH的面积是51平方厘米,那么平行四边形ABCD的面积是 108 平方厘米.
【解答】解:作如图辅助线HS∥AB、GQ∥AD、SE∥AD、QF∥AB,
设平行四边形面积为S平方厘米.
则RS=QT=AB,QR=ST=AD,HR=AB,RG=AD,FT=AB,ET=AD,
∴四边形EFGH的面积=[(×+×+×+×)﹣×]S=51.
即S=51,
解得S=108平分厘米.
故答案为 108.
15.如图,在?ABCD中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为 12.6 .
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=4,OA=OC,AB∥CD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
,
∴△AOE≌△COF(ASA),
∴CF=AE,OE=OE=1.8,
∴EF=OE+OF=3.6,
∴四边形BCFE的周长为:EF+BE+BC+CF=EF+BC+BE+AE=EF+BC+AB=3.6+4+5=12.6.
故答案为:12.6.
16.如图,?ABCD中,AD=10,AD边上的高为8,对角线交点为O,直线EF经过O,与AB、CD分别交于点E、F;直线GH经过点O,与AD、BC分别交于点G、H;直线MN经过点O,与AD、BC分别交于点M、N,则图中阴影部分的面积为 40 .
【解答】解:由题意可得:△GOM≌△HON,△DOF≌△BOE,△AEO≌△CFO,
则S△GOM=S△HON,S△DOF=S△BOE,S△AEO=S△CFO,
故图中阴影部分的面积为:S四边形ABCD=×8×10=40.
故答案为:40.
17.如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 25° .
【解答】解:∵?ABCD与?DCFE的周长相等,且CD=CD,
∴AD=DE,
∵∠DAE=∠DEA,
∵∠BAD=60°,∠F=110°,
∴∠ADC=120°,∠CDE═∠F=110°,
∴∠ADE=360°﹣120°﹣110°=130°,
∴∠DAE==25°,
故答案为:25°.
18.已知a、b、c、d为四边形的四边长,a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是 平行 四边形.
【解答】解:∵a2+b2+c2+d2=2ac+2bd
∴a2+b2+c2+d2﹣2ac﹣2bd=0
∴(a﹣b)2+(c﹣d)2=0
解得:a=b,c=d,
∴这个四边形的形状是平行四边形.
故答案为:平行.
19.如图,在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN于N,已知AB=10,AC=18,则MN的长是 4 .
【解答】解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND,
∴AD=AB=10,BN=ND,
∴DC=AC﹣AD=8,
∵BN=ND,BM=MC,
∴MN=CD=4,
故答案为:4.
20.如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是 .
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=3,
∴CE==2,
∴AB=,
故答案为:.
21.我们把四边形两条对角线中点的连线段称为奇异中位线.现有两个全等三角形,边长分别为3cm,4cm,5cm.将这两个三角形相等的边重合拼成凸四边形,如果凸四边形的奇异中位线的长不为0,那么奇异中位线的长是 cm.
【解答】解:∵32+42=9+16=25=52,
∴边长分别为3cm,4cm,5cm的三角形是直角三角形.
如图,将两个全等的直角△ABC与△DEF的斜边AC与DF重合,拼成凸四边形ABCE,AC与BE交于点O,M为AC的中点.
∵△ABC≌△DEF,
∴AB=AE=3cm,∠BAC=∠EDF,
∴BO=OE,AO⊥BE.
在Rt△AOB中,∵∠AOB=90°,
∴OA=AB?cos∠BAO=3×=,
∵AM=AC=,
∴OM=AM﹣OA=﹣=.
即奇异中位线的长是cm.
故答案为.
三.解答题(共5小题)
22.已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵△AOB的周长比△BOC的周长多8cm,
∴(OA+OB+AB)﹣(OB+OC+BC)=8cm,
即AB﹣BC=8cm,①
∵平行四边形ABCD的周长为60cm,
∴2(AB+BC)=60cm,②
∴由①②得到:AB=19cm,BC=11cm.
23.如图1是某公交汽车挡风玻璃的雨刮器,其工作原理如图2.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
【解答】证明:∵AB=CD、AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF⊥AD,
∴EF⊥BC.
24.如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF,判断四边形ADEF的形状,并加以证明.
【解答】答:四边形ADEF是平行四边形.
证明:∵点D,E分别是边BC,AC的中点,
∴DE∥BF,DE=AB,
∵AF=AB,
∴DE=AF,
∴四边形ADEF是平行四边形.
25.如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
【解答】(1)证明:在Rt△OAB中,D为OB的中点,
∴DO=DA,
∴∠DAO=∠DOA=30°,∠EOA=90°,
∴∠AEO=60°
又∵△OBC为等边三角形
∴∠BCO=∠AEO=60°,
∴BC∥AE,
∵∠BAO=∠COA=90°,
∴OC∥AB,
∴四边形ABCE是平行四边形.
(2)解:在Rt△ABO中,
∵∠OAB=90°,∠AOB=30°,AB=2,
∴OA=AB?tan60°=2×=.
在Rt△OAG中,OA2+OG2=AG2,设OG=x,
由折叠可知:AG=GC=4﹣x,可得,
解得,
∴OG=.
26.[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为.
[运用]
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 (2,1.5) .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
【解答】解:(1)M(,),即M(2,1.5).
(2)如图所示:
根据平行四边形的对角线互相平分可得:
设D点的坐标为(x,y),
∵以点A、B、C、D构成的四边形是平行四边形,
①当AB为对角线时,
∵A(﹣1,2),B(3,1),C(1,4),
∴BC=,
∴AD=,
∵﹣1+3﹣1=1,2+1﹣4=﹣1,
∴D点坐标为(1,﹣1),
②当BC为对角线时,
∵A(﹣1,2),B(3,1),C(1,4),
∴AC=2,BD=2,
D点坐标为(5,3).
③当AC为对角线时,
∵A(﹣1,2),B(3,1),C(1,4),
∴AB==,
∴CD=,
D点坐标为:(1﹣3﹣1,4﹣1+2),即(﹣3,5),
综上所述,符合要求的点有:D'(1,﹣1),D″(﹣3,5),D″′(5,3).
一.选择题(共10小题)
1.?ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )
A.∠A=100°,∠D=80° B.∠A=80°,∠D=100°
C.∠B=80°,∠D=80° D.∠A=100°,∠D=100°
2.如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )
A.2:1 B.3:1 C.3:2 D.4:3
3.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AB=CD
C.AB∥CD,AD∥BC D.AB=CD,AD∥BC
4.如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
A.10cm B.8cm C.6cm D.4cm
5.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
A.1种 B.2种 C.3种 D.无数种
6.如图,已知在四边形ABCD中,AB∥CD,AB=CD,E为AB上一点,过点E作EF∥BC,交CD于点F,G为AD上一点,H为BC上一点,连接CG,AH.若GD=BH,则图中的平行四边形有( )
A.2个 B.3个 C.4个 D.6个
7.已知平行四边形一边长为8,一条对角线长为6,则另一条对角线α满足( )
A.10<α<22 B.4<α<20 C.4<α<28 D.2<α<14
8.在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别是(0,0)、(3,0)、(4,2),则顶点D的坐标为( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
9.如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4 B.3 C.2 D.
10.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;
⑤∠APB的大小.其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
二.填空题(共11小题)
11.在?ABCD中,AB=6cm,BC=8cm,则?ABCD的周长为 cm.
12.如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 .
13.如图,四边形ABCD中,对角线BD⊥AD,BD⊥BC,AD=11﹣x,BC=x﹣5,则当x= 时,四边形ABCD是平行四边形.
14.如图,F、G、H分别是平行四边形ABCD的边BC、CD、AD上的三等分点,E是AB边的中点,已知四边形EFGH的面积是51平方厘米,那么平行四边形ABCD的面积是 平方厘米.
15.如图,在?ABCD中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为 .
16.如图,?ABCD中,AD=10,AD边上的高为8,对角线交点为O,直线EF经过O,与AB、CD分别交于点E、F;直线GH经过点O,与AD、BC分别交于点G、H;直线MN经过点O,与AD、BC分别交于点M、N,则图中阴影部分的面积为 .
17.如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 .
18.已知a、b、c、d为四边形的四边长,a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是 四边形.
19.如图,在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN于N,已知AB=10,AC=18,则MN的长是 .
20.如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是 .
21.我们把四边形两条对角线中点的连线段称为奇异中位线.现有两个全等三角形,边长分别为3cm,4cm,5cm.将这两个三角形相等的边重合拼成凸四边形,如果凸四边形的奇异中位线的长不为0,那么奇异中位线的长是 cm.
三.解答题(共5小题)
22.已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
23.如图1是某公交汽车挡风玻璃的雨刮器,其工作原理如图2.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
24.如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF,判断四边形ADEF的形状,并加以证明.
25.如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
26.[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为.
[运用]
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
八下数学培优提高 第十八章 平行四边形的性质与判定
参考答案与试题解析
一.选择题(共10小题)
1.?ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )
A.∠A=100°,∠D=80° B.∠A=80°,∠D=100°
C.∠B=80°,∠D=80° D.∠A=100°,∠D=100°
【解答】解:∵∠A与∠B是邻角,
∴∠A=180°﹣∠B=80°,
∴∠D=∠B=100°
故选:B.
2.如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于( )
A.2:1 B.3:1 C.3:2 D.4:3
【解答】解:过E作EM∥AB与GC交于点M,
∴△EMF≌△DGF,
∴EM=GD,
∵DE是中位线,
∴CE=AC,
又∵EM∥AG,
∴EM:AG=CE:AC=1:2,
又∵EM=GD,
∴AG:GD=2:1.
故选:A.
3.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AB=CD
C.AB∥CD,AD∥BC D.AB=CD,AD∥BC
【解答】解:A、∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
故A可以判断四边形ABCD是平行四边形.
B、∵AB∥CD,AB=CD,
∴∴四边形ABCD是平行四边形,
故B可以判断四边形ABCD是平行四边形.
C、∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
故C可以判断四边形ABCD是平行四边形.
D、∵AB=CD,AD∥BC,
∴四边形ABCD可能是平行四边形,有可能是等腰梯形.
故D不可以判断四边形ABCD是平行四边形.
故选:D.
4.如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
A.10cm B.8cm C.6cm D.4cm
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠DAE=∠BAE,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
设AB=CD=xcm,则AD=BC=(x+2)cm,
∵?ABCD的周长为20cm,
∴x+x+2=10,
解得:x=4,
即AB=4cm,
故选:D.
5.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
A.1种 B.2种 C.3种 D.无数种
【解答】解:因为平行四边形是中心对称图形,任意一条过平行四边形对角线交点的直线都平分四边形的面积,则这样的折纸方法共有无数种.
故选:D.
6.如图,已知在四边形ABCD中,AB∥CD,AB=CD,E为AB上一点,过点E作EF∥BC,交CD于点F,G为AD上一点,H为BC上一点,连接CG,AH.若GD=BH,则图中的平行四边形有( )
A.2个 B.3个 C.4个 D.6个
【解答】解:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
又∵EF∥BC,
∴四边形AEFD、四边形BCFE均为平行四边形,
∵GD=BH,AD=BC,
∴AG=CH,
又∵AG∥CH,
∴四边形AHCG是平行四边形,
又∵EF∥BC,
∴四边形AMNG、四边形MNCH均为平行四边形,
∴共有6个平行四边形,
故选:D.
7.已知平行四边形一边长为8,一条对角线长为6,则另一条对角线α满足( )
A.10<α<22 B.4<α<20 C.4<α<28 D.2<α<14
【解答】解:如图,已知平行四边形中,AB=8,AC=6,求BD的取值范围,即α的取值范围.
∵四边形ABCD是平行四边形,
∴α=2OB,AC=2OA=6,
∴OB=α,OA=3,
∴在△AOB中:AB﹣OA<OB<AB+OA
即:10<α<22,
故选:A.
8.在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别是(0,0)、(3,0)、(4,2),则顶点D的坐标为( )
A.(7,2) B.(5,4) C.(1,2) D.(2,1)
【解答】解:如图:
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∵?ABCD的顶点A、B、C的坐标分别是(0,0)、(3,0)、(4,2),
∴顶点D的坐标为(1,2).
故选:C.
9.如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4 B.3 C.2 D.
【解答】解:∵四边形ABCD是菱形,
∴BC=CD,∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴BC×AE=CD×AF,∠BAE=∠DAF=30°,
∴AE=AF,
∵∠B=60°,
∴∠BAD=120°,
∴∠EAF=120°﹣30°﹣30°=60°,
∴△AEF是等边三角形,
∴AE=EF,∠AEF=60°,
∵AB=4,
∴BE=2,
∴AE==2,
∴EF=AE=2,
过A作AM⊥EF,
∴AM=AE?sin60°=3,
∴△AEF的面积是:EF?AM=×2×3=3.
故选:B.
10.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
【解答】解:∵点A,B为定点,点M,N分别为PA,PB的中点,
∴MN是△PAB的中位线,
∴MN=AB,
即线段MN的长度不变,故①错误;
PA、PB的长度随点P的移动而变化,
所以,△PAB的周长会随点P的移动而变化,故②正确;
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变,故③错误;
直线MN,AB之间的距离不随点P的移动而变化,故④错误;
∠APB的大小点P的移动而变化,故⑤正确.
综上所述,会随点P的移动而变化的是②⑤.
故选:B.
二.填空题(共11小题)
11.在?ABCD中,AB=6cm,BC=8cm,则?ABCD的周长为 28 cm.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD=6,BC=AD=8,
∴平行四边形ABCD的周长是AB+BC+CD+AD=6+8+6+8=28cm.
故答案为:28.
12.如图所示,在?ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为 50° .
【解答】解:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠C=∠ABF.
又∵∠C=40°,
∴∠ABF=40°.
∵EF⊥BF,
∴∠F=90°,
∴∠BEF=90°﹣40°=50°.
故答案是:50°.
13.如图,四边形ABCD中,对角线BD⊥AD,BD⊥BC,AD=11﹣x,BC=x﹣5,则当x= 8 时,四边形ABCD是平行四边形.
【解答】解:∵BD⊥AD,BD⊥BC,
∴AD∥BC,
只要AD=BC,四边形ABCD是平行四边形.
AD=BC
11﹣x=x﹣5
x=8.
故答案为:8.
14.如图,F、G、H分别是平行四边形ABCD的边BC、CD、AD上的三等分点,E是AB边的中点,已知四边形EFGH的面积是51平方厘米,那么平行四边形ABCD的面积是 108 平方厘米.
【解答】解:作如图辅助线HS∥AB、GQ∥AD、SE∥AD、QF∥AB,
设平行四边形面积为S平方厘米.
则RS=QT=AB,QR=ST=AD,HR=AB,RG=AD,FT=AB,ET=AD,
∴四边形EFGH的面积=[(×+×+×+×)﹣×]S=51.
即S=51,
解得S=108平分厘米.
故答案为 108.
15.如图,在?ABCD中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为 12.6 .
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=4,OA=OC,AB∥CD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
,
∴△AOE≌△COF(ASA),
∴CF=AE,OE=OE=1.8,
∴EF=OE+OF=3.6,
∴四边形BCFE的周长为:EF+BE+BC+CF=EF+BC+BE+AE=EF+BC+AB=3.6+4+5=12.6.
故答案为:12.6.
16.如图,?ABCD中,AD=10,AD边上的高为8,对角线交点为O,直线EF经过O,与AB、CD分别交于点E、F;直线GH经过点O,与AD、BC分别交于点G、H;直线MN经过点O,与AD、BC分别交于点M、N,则图中阴影部分的面积为 40 .
【解答】解:由题意可得:△GOM≌△HON,△DOF≌△BOE,△AEO≌△CFO,
则S△GOM=S△HON,S△DOF=S△BOE,S△AEO=S△CFO,
故图中阴影部分的面积为:S四边形ABCD=×8×10=40.
故答案为:40.
17.如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 25° .
【解答】解:∵?ABCD与?DCFE的周长相等,且CD=CD,
∴AD=DE,
∵∠DAE=∠DEA,
∵∠BAD=60°,∠F=110°,
∴∠ADC=120°,∠CDE═∠F=110°,
∴∠ADE=360°﹣120°﹣110°=130°,
∴∠DAE==25°,
故答案为:25°.
18.已知a、b、c、d为四边形的四边长,a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是 平行 四边形.
【解答】解:∵a2+b2+c2+d2=2ac+2bd
∴a2+b2+c2+d2﹣2ac﹣2bd=0
∴(a﹣b)2+(c﹣d)2=0
解得:a=b,c=d,
∴这个四边形的形状是平行四边形.
故答案为:平行.
19.如图,在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN于N,已知AB=10,AC=18,则MN的长是 4 .
【解答】解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND,
∴AD=AB=10,BN=ND,
∴DC=AC﹣AD=8,
∵BN=ND,BM=MC,
∴MN=CD=4,
故答案为:4.
20.如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是 .
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=3,
∴CE==2,
∴AB=,
故答案为:.
21.我们把四边形两条对角线中点的连线段称为奇异中位线.现有两个全等三角形,边长分别为3cm,4cm,5cm.将这两个三角形相等的边重合拼成凸四边形,如果凸四边形的奇异中位线的长不为0,那么奇异中位线的长是 cm.
【解答】解:∵32+42=9+16=25=52,
∴边长分别为3cm,4cm,5cm的三角形是直角三角形.
如图,将两个全等的直角△ABC与△DEF的斜边AC与DF重合,拼成凸四边形ABCE,AC与BE交于点O,M为AC的中点.
∵△ABC≌△DEF,
∴AB=AE=3cm,∠BAC=∠EDF,
∴BO=OE,AO⊥BE.
在Rt△AOB中,∵∠AOB=90°,
∴OA=AB?cos∠BAO=3×=,
∵AM=AC=,
∴OM=AM﹣OA=﹣=.
即奇异中位线的长是cm.
故答案为.
三.解答题(共5小题)
22.已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵△AOB的周长比△BOC的周长多8cm,
∴(OA+OB+AB)﹣(OB+OC+BC)=8cm,
即AB﹣BC=8cm,①
∵平行四边形ABCD的周长为60cm,
∴2(AB+BC)=60cm,②
∴由①②得到:AB=19cm,BC=11cm.
23.如图1是某公交汽车挡风玻璃的雨刮器,其工作原理如图2.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
【解答】证明:∵AB=CD、AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF⊥AD,
∴EF⊥BC.
24.如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF,判断四边形ADEF的形状,并加以证明.
【解答】答:四边形ADEF是平行四边形.
证明:∵点D,E分别是边BC,AC的中点,
∴DE∥BF,DE=AB,
∵AF=AB,
∴DE=AF,
∴四边形ADEF是平行四边形.
25.如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
【解答】(1)证明:在Rt△OAB中,D为OB的中点,
∴DO=DA,
∴∠DAO=∠DOA=30°,∠EOA=90°,
∴∠AEO=60°
又∵△OBC为等边三角形
∴∠BCO=∠AEO=60°,
∴BC∥AE,
∵∠BAO=∠COA=90°,
∴OC∥AB,
∴四边形ABCE是平行四边形.
(2)解:在Rt△ABO中,
∵∠OAB=90°,∠AOB=30°,AB=2,
∴OA=AB?tan60°=2×=.
在Rt△OAG中,OA2+OG2=AG2,设OG=x,
由折叠可知:AG=GC=4﹣x,可得,
解得,
∴OG=.
26.[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为.
[运用]
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 (2,1.5) .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
【解答】解:(1)M(,),即M(2,1.5).
(2)如图所示:
根据平行四边形的对角线互相平分可得:
设D点的坐标为(x,y),
∵以点A、B、C、D构成的四边形是平行四边形,
①当AB为对角线时,
∵A(﹣1,2),B(3,1),C(1,4),
∴BC=,
∴AD=,
∵﹣1+3﹣1=1,2+1﹣4=﹣1,
∴D点坐标为(1,﹣1),
②当BC为对角线时,
∵A(﹣1,2),B(3,1),C(1,4),
∴AC=2,BD=2,
D点坐标为(5,3).
③当AC为对角线时,
∵A(﹣1,2),B(3,1),C(1,4),
∴AB==,
∴CD=,
D点坐标为:(1﹣3﹣1,4﹣1+2),即(﹣3,5),
综上所述,符合要求的点有:D'(1,﹣1),D″(﹣3,5),D″′(5,3).
