新课标人教A版 高一数学(必修4) 2.2.3向量数乘运算及其几何意义(21张PPT)
文档属性
| 名称 | 新课标人教A版 高一数学(必修4) 2.2.3向量数乘运算及其几何意义(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-04 08:35:00 | ||
图片预览







文档简介
课件21张PPT。2.2.3向量数乘运算及其几何意义高中数学人教A版必修4学习目标
1.知识与技能:
通过实例,掌握向量数乘的运算,并理解其几何意义,以及两个向量共线的含义;掌握共线向量的充要条件。
2.过程与方法:
由几个向量的和得出向量数乘运算的含义,从特殊到一般,经历向量数乘概念的形成,探究共线向量的充要条件,培养学生类比归纳的能力。
3.情感态度与价值观:
初步体会实数与向量的乘积的含义及其几何意义,形成归纳、猜想与论证的能力。
学习重点:
1.实数与向量积的意义.
2.实数与向量积的运算律.
3.两个向量共线的等价条件及其运用.
学习难点:
1.理解向量数乘运算的几何意义
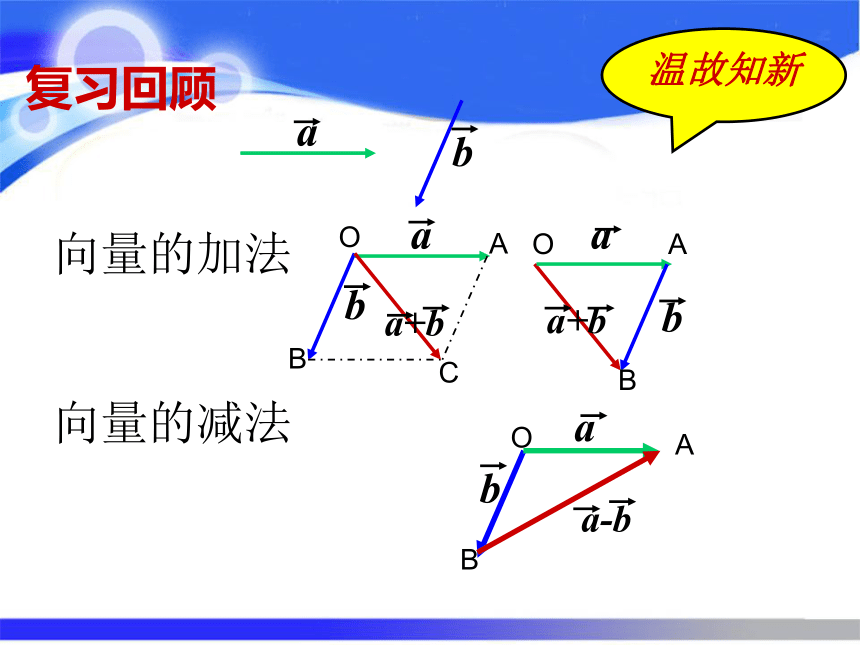
2.对向量共线的等价条件的理解运用.aba-b复习回顾向量的减法向量的加法a+ba+bOABCAOBAOB温故知新探究:已知非零向量作出:你能说明它们的几何意义吗?和知识引入类似数的乘法,我们把 3a方向与a方向相同,|3a|=___|a|3探究探 究一、实数与向量的积的定义: 知识新授数乘向量的几何意义就是把向量 沿 的方向或反
方向放大或缩短.若 ,当 沿 的方
向放大了 倍.当 沿 的方向缩短了 倍.
当 ,沿 的反方向放大了 倍.当
沿 的反方向缩短了 倍.由其几何意义可以看出
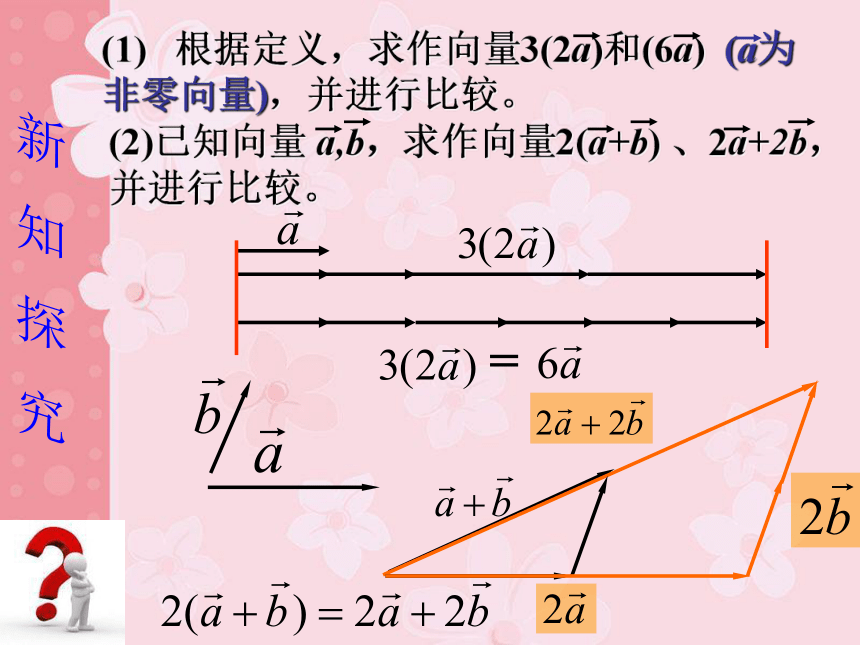
用数乘向量能解决几何中的相似问题. 数乘向量的几何意义(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。已知向量 a,b,求作向量2(a+b) 、2a+2b,
并进行比较。=新 知 探 究二、向量数乘的运算律:知识新授例5 计算:审题指导:此类问题只需利用向量数乘、加法、减法的运算律化简即得结果。规律方法:向量数乘运算类似于多项式的运算,主要是“合并 同类项”“提公因式”,但这里的“同类项”及“公因式”都 是指向量,实数看成是向量的系数。夯实基础
深入探究 引入向量数乘后,你能发现数乘向量与原向量之间的位置关系吗?思 考新知探究、提出问题三、共线向量定理:知
识
新
授思路点拨:先利用向量加法作出OA、OB、OC,通过观察A、B、C三点的位置关系,再用向量共线证明三点共线 . 例6 如图,已知任意两个非零向量 你能判断A、B、C三点之间的位置关系吗?为什么?知识应用典型例题A 解:如图分别作向量OA、OB、OC,过点A、C作直线AC,观察发现点B始终在直线AC上,猜想A、B、C三点共线。例7如图, 的两条对角线相交于点M, 且ADCBM解:在方法梳理1.证明三点共线的方法:2.解决与向量共线有关的存在性问题的方法:通常先假设存在,再根据已知条件找等量关系列方程求解.若有解且与题目条件无矛盾则存在,反之不存在.3.本节学习中用到哪些思想方法:特殊到一般,归纳、猜想、类比,分类讨论,等价转化.当堂检测1.下列命题中,正确的是______.(填序号)小结回顾:
方向放大或缩短.若 ,当 沿 的方
向放大了 倍.当 沿 的方向缩短了 倍.
当 ,沿 的反方向放大了 倍.当
沿 的反方向缩短了 倍.由其几何意义可以看出
用数乘向量能解决几何中的相似问题. 数乘向量的几何意义(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。已知向量 a,b,求作向量2(a+b) 、2a+2b,
并进行比较。=新 知 探 究二、向量数乘的运算律:知识新授例5 计算:审题指导:此类问题只需利用向量数乘、加法、减法的运算律化简即得结果。规律方法:向量数乘运算类似于多项式的运算,主要是“合并 同类项”“提公因式”,但这里的“同类项”及“公因式”都 是指向量,实数看成是向量的系数。夯实基础
深入探究 引入向量数乘后,你能发现数乘向量与原向量之间的位置关系吗?思 考新知探究、提出问题三、共线向量定理:知
识
新
授思路点拨:先利用向量加法作出OA、OB、OC,通过观察A、B、C三点的位置关系,再用向量共线证明三点共线 . 例6 如图,已知任意两个非零向量 你能判断A、B、C三点之间的位置关系吗?为什么?知识应用典型例题A 解:如图分别作向量OA、OB、OC,过点A、C作直线AC,观察发现点B始终在直线AC上,猜想A、B、C三点共线。例7如图, 的两条对角线相交于点M, 且ADCBM解:在方法梳理1.证明三点共线的方法:2.解决与向量共线有关的存在性问题的方法:通常先假设存在,再根据已知条件找等量关系列方程求解.若有解且与题目条件无矛盾则存在,反之不存在.3.本节学习中用到哪些思想方法:特殊到一般,归纳、猜想、类比,分类讨论,等价转化.当堂检测1.下列命题中,正确的是______.(填序号)小结回顾:
