四年级下册数学一课一练4.2三角形分类西师大版(含答案)
文档属性
| 名称 | 四年级下册数学一课一练4.2三角形分类西师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 39.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-04 09:51:24 | ||
图片预览


文档简介
四年级下册数学一课一练-4.2三角形分类
一、单选题
1.等腰三角形有( )条边相等
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
2.一个等腰三角形的底角是80°,它的顶角是(??? )。
A.?80°??????????????????????????????????????????B.?100°??????????????????????????????????????????C.?20°
3.(?????? )个角是锐角的三角形,是锐角三角形。
A.?三?????????????????????????????????????????????B.?二?????????????????????????????????????????????C.?一
4.一个三角形中,最多有( )个直角。
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
5.有一个直角三角形,两个锐角分别是(?? )
A.?48°和52。??????????????????????????B.?38°和42°??????????????????????????C.?48°和42°??????????????????????????D.?60°和35°
6.一个三角形至少有()个锐角.(?? )
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
二、判断题
7.所有三角形的内角和都是180°。(??? )
8.所有的等边三角形一定是锐角三角形。
9.判断对错
(1)三角形的三条边都可以作底边,因此三角形能作三条高.
(2)直角三角形的两条直角边可以分别看作这个直角三角形的底和高.
(3)等腰三角形都是等边三角形.
(4)等腰三角形都是锐角三角形.
10.直角三角形的两条直角边互为底和高。
三、填空题
11.直角三角形的面积是15平方厘米,一条直角边长是5厘米,另一直角边长________厘米。
12.一个直角三角形,有一个锐角是35°,另一个锐角是________?。
13.三角形的内角和是________度,等腰三角形的一个底角是80度,顶角是________度.
14.一个三角形的两个内角分别是45°和90°,另一个内角是________度,这是一个________三角形。
15.一个直角三角形的较小的锐角是30度,另一个锐角的度数是________度.
四、计算题
16.求下面三角形中未知角的度数。已知:∠1=80°,∠2=68°。求:∠3=? ∠4=?
五、解答题
17.请你分别画出一个锐角三角形和一个钝角三角形.
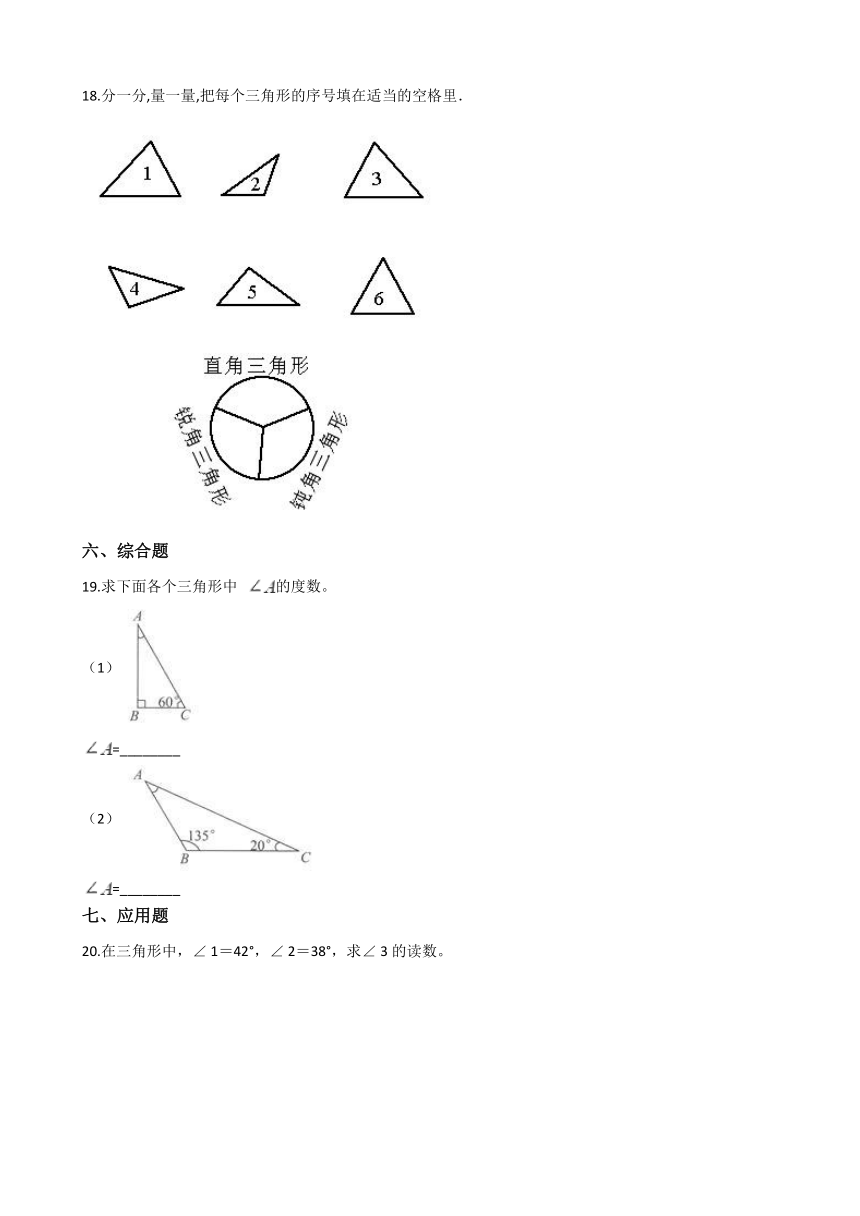
18.分一分,量一量,把每个三角形的序号填在适当的空格里.
六、综合题
19.求下面各个三角形中 的度数。
(1)
=________
(2)
=________
七、应用题
20.在三角形中,∠ 1=42°,∠ 2=38°,求∠ 3的读数。
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】等腰三角形两条边相等。 故答案为:B
【分析】根据等腰三角形的性质解答即可。
2.【答案】 C
【解析】【解答】解:等腰三角形的两个底角相等,所以两个底角之和为80°×2=160°,三角形的内角和是180°,所以它的顶角是:180°-160°=20°。 故答案为:C。
【分析】等腰三角形的两条腰相等,两个底角相等。
3.【答案】 A
【解析】【解答】三个角是锐角的三角形,是锐角三角形。 故答案为:A。
【分析】三个角都是锐角的三角形是锐角三角形,也可以理解为一个三角形中,最大的角是锐角的三角形是锐角三角形。
4.【答案】A
【解析】【解答】何为直角三角形,有一个角是直角的三角形为直角三角形,所以,一个三角形中最多有一个直角。
【分析】与三角形内角和有关的知识。
5.【答案】 C
【解析】【解答】解:直角三角形两锐角的和是90°,选项C中两个角的和是90度. 故答案为:C.
【分析】直角三角形中有一个角是直角,剩余两个角的和是90度,据此解答即可.
6.【答案】 B
【解析】【解答】解:一个三角形最多有一个直角或一个钝角,另外两个角都是锐角,所以一个三角形至少有2个锐角. 故答案为:B
【分析】三角形内角和是180°,所以三角形至少有2个锐角,最多三个都是锐角.
二、判断题
7.【答案】 正确
【解析】【解答】所有三角形的内角和都是180°,此题说法正确. 故答案为:正确.
【分析】三角形的内角和是180°,据此判断.
8.【答案】 正确
【解析】【解答】解:所有的等边三角形一定是锐角三角形。原题说法正确。 故答案为:正确。 【分析】等边三角形的三个角都是60°,都是锐角,所以等边三角形是锐角三角形。
9.【答案】(1)1 (2)1 (3)0 (4)0
【解析】【解答】解:1.根据三角形高的意义可得三角形的三条边都可以作底边,所以三角形能作三条高,可见原题说法正确; 2.直角三角形的两条直角边互相垂直,所以两条直角边可以分别看作这个直角三角形的底和高,可见原题说法正确; 3.等边三角形都是等腰三角形,反之不一定,可见原题说法错误; 4.等腰三角形的顶角可以是直角或钝角,所以原题说法错误. 故答案为:1.正确;2.正确;3.错误;4.错误.
【分析】对于1题,根据三角形的高的意义进行判断即可;对于2题,根据直角边的两条直角边的特性进行判断即可;对于3题,等边三角形都是等腰三角形,但等腰三角形不都是等边三角形,据此判断即可;对于4题,等腰三角形的顶角不确定,顶角可以是直角、钝角,所以不能确定是哪类三角形,据此判断即可.
10.【答案】 正确
【解析】【解答】 直角三角形的两条直角边互为底和高,此题说法正确. 故答案为:正确.
【分析】因为直角三角形的两条直角边是互相垂直的关系,所以直角三角形的两条直角边互为底和高,据此判断.
三、填空题
11.【答案】 6
【解析】【解答】解:另一直角边长为:
15×2÷5=6(厘米)
12.【答案】55°
【解析】【解答】解:90°-35°=55° 故答案为:55° 【分析】直角三角形中两个锐角的度数和是90°,所以用90°减去已知的锐角即可求出另一个锐角.
13.【答案】 180;20
【解析】【解答】解:因为其底角为80°,所以其顶角=180°﹣80°×2=20°.
所以三角形的内角和是 180°;一个等腰三角形的一个底角是80°,顶角的度数是20°.
故答案为:180,20.
【分析】根据三角形的内角和定理:三角形的内角和为180°,已知给出了一个底角为80°,利用180°﹣80°×2=20°即可解本题.此题主要考查了学生的三角形的内角和定理:三角形的内角和为180°.利用三角形的内角和求角度是一种很重要的方法,要熟练掌握.
14.【答案】 45;直角
【解析】【解答】180°-45°-90°=45°,这是一个直角三角形。 故答案为:45、直角
【分析】三角形内角和分别减去两个内角度数,就等于另一个内角度数;有一个角是直角的三角形是直角三角形。
15.【答案】 60
【解析】【解答】解:90°-30°=60° 故答案为:60.
【分析】直角三角形两个锐角的和是90度,用90度减去已知角的度数即可求出另一个角的度数.
四、计算题
16.【答案】解:∠3=32°,∠4=148°
【解析】【解答】∠3=180°-∠1-∠2=180°-80°-68°=32°,∠4=180°-∠3=180°-32°=148° 故答案为:∠3=32°,∠4=148° 【分析】因为三角形内角和是180°,所以∠3=180°-∠1-∠2;又因为∠3+∠4=180°,所以∠4=180°-∠3。
五、解答题
17.【答案】如图
【解析】解答:解:如图: 分析:三个角都是锐角的三角形,叫锐角三角形;有一个角是钝角的三角形,叫钝角三角形;据此分别画出即可.
18.【答案】解:
【解析】【分析】最大角是直角的三角形是直角三角形,直角三角形有4和5;最大角是钝角的三角形是钝角三角形,钝角三角形有2;三个角都是锐角的三角形是锐角三角形,锐角三角形有1、3、6.
六、综合题
19.【答案】(1)30° (2)25°
【解析】【解答】解:(1)90°-60°=30°;(2)180°-135°-20°=25°. 故答案为:30°;25°
【分析】(1)直角三角形两个锐角的度数和是90°,用90°减去其中一个锐角的度数就是另一个锐角的度数;(2)用三角形内角和180°减去已知的两个角的度数即可求出未知角的度数.
七、应用题
20.【答案】由三角形的内角和为180°,在三角形中,∠1=42°,∠2=38°,列式可得
∠3=180°-42°-38°=100°
答:∠3的读数为100°。
【解析】【解答】由三角形的内角和为180°,在三角形中,∠1=42°,∠2=38°,列式可得
∠3=180°-42°-38°=100°
答:∠3的读数为100°
【分析】本题主要考查三角形的性质和三角形的内角和定理
一、单选题
1.等腰三角形有( )条边相等
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
2.一个等腰三角形的底角是80°,它的顶角是(??? )。
A.?80°??????????????????????????????????????????B.?100°??????????????????????????????????????????C.?20°
3.(?????? )个角是锐角的三角形,是锐角三角形。
A.?三?????????????????????????????????????????????B.?二?????????????????????????????????????????????C.?一
4.一个三角形中,最多有( )个直角。
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
5.有一个直角三角形,两个锐角分别是(?? )
A.?48°和52。??????????????????????????B.?38°和42°??????????????????????????C.?48°和42°??????????????????????????D.?60°和35°
6.一个三角形至少有()个锐角.(?? )
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
二、判断题
7.所有三角形的内角和都是180°。(??? )
8.所有的等边三角形一定是锐角三角形。
9.判断对错
(1)三角形的三条边都可以作底边,因此三角形能作三条高.
(2)直角三角形的两条直角边可以分别看作这个直角三角形的底和高.
(3)等腰三角形都是等边三角形.
(4)等腰三角形都是锐角三角形.
10.直角三角形的两条直角边互为底和高。
三、填空题
11.直角三角形的面积是15平方厘米,一条直角边长是5厘米,另一直角边长________厘米。
12.一个直角三角形,有一个锐角是35°,另一个锐角是________?。
13.三角形的内角和是________度,等腰三角形的一个底角是80度,顶角是________度.
14.一个三角形的两个内角分别是45°和90°,另一个内角是________度,这是一个________三角形。
15.一个直角三角形的较小的锐角是30度,另一个锐角的度数是________度.
四、计算题
16.求下面三角形中未知角的度数。已知:∠1=80°,∠2=68°。求:∠3=? ∠4=?
五、解答题
17.请你分别画出一个锐角三角形和一个钝角三角形.
18.分一分,量一量,把每个三角形的序号填在适当的空格里.
六、综合题
19.求下面各个三角形中 的度数。
(1)
=________
(2)
=________
七、应用题
20.在三角形中,∠ 1=42°,∠ 2=38°,求∠ 3的读数。
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】等腰三角形两条边相等。 故答案为:B
【分析】根据等腰三角形的性质解答即可。
2.【答案】 C
【解析】【解答】解:等腰三角形的两个底角相等,所以两个底角之和为80°×2=160°,三角形的内角和是180°,所以它的顶角是:180°-160°=20°。 故答案为:C。
【分析】等腰三角形的两条腰相等,两个底角相等。
3.【答案】 A
【解析】【解答】三个角是锐角的三角形,是锐角三角形。 故答案为:A。
【分析】三个角都是锐角的三角形是锐角三角形,也可以理解为一个三角形中,最大的角是锐角的三角形是锐角三角形。
4.【答案】A
【解析】【解答】何为直角三角形,有一个角是直角的三角形为直角三角形,所以,一个三角形中最多有一个直角。
【分析】与三角形内角和有关的知识。
5.【答案】 C
【解析】【解答】解:直角三角形两锐角的和是90°,选项C中两个角的和是90度. 故答案为:C.
【分析】直角三角形中有一个角是直角,剩余两个角的和是90度,据此解答即可.
6.【答案】 B
【解析】【解答】解:一个三角形最多有一个直角或一个钝角,另外两个角都是锐角,所以一个三角形至少有2个锐角. 故答案为:B
【分析】三角形内角和是180°,所以三角形至少有2个锐角,最多三个都是锐角.
二、判断题
7.【答案】 正确
【解析】【解答】所有三角形的内角和都是180°,此题说法正确. 故答案为:正确.
【分析】三角形的内角和是180°,据此判断.
8.【答案】 正确
【解析】【解答】解:所有的等边三角形一定是锐角三角形。原题说法正确。 故答案为:正确。 【分析】等边三角形的三个角都是60°,都是锐角,所以等边三角形是锐角三角形。
9.【答案】(1)1 (2)1 (3)0 (4)0
【解析】【解答】解:1.根据三角形高的意义可得三角形的三条边都可以作底边,所以三角形能作三条高,可见原题说法正确; 2.直角三角形的两条直角边互相垂直,所以两条直角边可以分别看作这个直角三角形的底和高,可见原题说法正确; 3.等边三角形都是等腰三角形,反之不一定,可见原题说法错误; 4.等腰三角形的顶角可以是直角或钝角,所以原题说法错误. 故答案为:1.正确;2.正确;3.错误;4.错误.
【分析】对于1题,根据三角形的高的意义进行判断即可;对于2题,根据直角边的两条直角边的特性进行判断即可;对于3题,等边三角形都是等腰三角形,但等腰三角形不都是等边三角形,据此判断即可;对于4题,等腰三角形的顶角不确定,顶角可以是直角、钝角,所以不能确定是哪类三角形,据此判断即可.
10.【答案】 正确
【解析】【解答】 直角三角形的两条直角边互为底和高,此题说法正确. 故答案为:正确.
【分析】因为直角三角形的两条直角边是互相垂直的关系,所以直角三角形的两条直角边互为底和高,据此判断.
三、填空题
11.【答案】 6
【解析】【解答】解:另一直角边长为:
15×2÷5=6(厘米)
12.【答案】55°
【解析】【解答】解:90°-35°=55° 故答案为:55° 【分析】直角三角形中两个锐角的度数和是90°,所以用90°减去已知的锐角即可求出另一个锐角.
13.【答案】 180;20
【解析】【解答】解:因为其底角为80°,所以其顶角=180°﹣80°×2=20°.
所以三角形的内角和是 180°;一个等腰三角形的一个底角是80°,顶角的度数是20°.
故答案为:180,20.
【分析】根据三角形的内角和定理:三角形的内角和为180°,已知给出了一个底角为80°,利用180°﹣80°×2=20°即可解本题.此题主要考查了学生的三角形的内角和定理:三角形的内角和为180°.利用三角形的内角和求角度是一种很重要的方法,要熟练掌握.
14.【答案】 45;直角
【解析】【解答】180°-45°-90°=45°,这是一个直角三角形。 故答案为:45、直角
【分析】三角形内角和分别减去两个内角度数,就等于另一个内角度数;有一个角是直角的三角形是直角三角形。
15.【答案】 60
【解析】【解答】解:90°-30°=60° 故答案为:60.
【分析】直角三角形两个锐角的和是90度,用90度减去已知角的度数即可求出另一个角的度数.
四、计算题
16.【答案】解:∠3=32°,∠4=148°
【解析】【解答】∠3=180°-∠1-∠2=180°-80°-68°=32°,∠4=180°-∠3=180°-32°=148° 故答案为:∠3=32°,∠4=148° 【分析】因为三角形内角和是180°,所以∠3=180°-∠1-∠2;又因为∠3+∠4=180°,所以∠4=180°-∠3。
五、解答题
17.【答案】如图
【解析】解答:解:如图: 分析:三个角都是锐角的三角形,叫锐角三角形;有一个角是钝角的三角形,叫钝角三角形;据此分别画出即可.
18.【答案】解:
【解析】【分析】最大角是直角的三角形是直角三角形,直角三角形有4和5;最大角是钝角的三角形是钝角三角形,钝角三角形有2;三个角都是锐角的三角形是锐角三角形,锐角三角形有1、3、6.
六、综合题
19.【答案】(1)30° (2)25°
【解析】【解答】解:(1)90°-60°=30°;(2)180°-135°-20°=25°. 故答案为:30°;25°
【分析】(1)直角三角形两个锐角的度数和是90°,用90°减去其中一个锐角的度数就是另一个锐角的度数;(2)用三角形内角和180°减去已知的两个角的度数即可求出未知角的度数.
七、应用题
20.【答案】由三角形的内角和为180°,在三角形中,∠1=42°,∠2=38°,列式可得
∠3=180°-42°-38°=100°
答:∠3的读数为100°。
【解析】【解答】由三角形的内角和为180°,在三角形中,∠1=42°,∠2=38°,列式可得
∠3=180°-42°-38°=100°
答:∠3的读数为100°
【分析】本题主要考查三角形的性质和三角形的内角和定理
