人教八下数学19.3课题学习《选择方案》名师教案
文档属性
| 名称 | 人教八下数学19.3课题学习《选择方案》名师教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 128.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-04 13:01:49 | ||
图片预览


文档简介
19.3 课题学习 选择方案
一、教学目标
1.核心素养: 通过在实际问题中建立函数模型,根据所列函数解析式的性质,选择合理方案解决问题的学习,结合实际问题的数学信息,进行合情推理,提升建立数学模型的能力,发展应用意识.
2.学习目标
(1)巩固一次函数知识,进一步明确一次函数与不等式相结合的实际问题 (?http:?/??/?zk.canpoint.cn?/?" \o "欢迎登陆全品中考网?)处理方法.灵活运用变量之间的关系建立函数模型.
(2)让学生通过“选择上网收费方式”,提高运用函数知识解决实际问题的能力.
(3)让学生通过“怎样租车”,提高运用函数知识解决实际问题的能力.
3.学习重点
(1)培养学生自主分析问题 (?http:?/??/?zk.canpoint.cn?/?" \o "欢迎登陆全品中考网?)的实际背景中包含的变量及对应关系.
(2)运用一次函数的性质解决生活中的最佳方案.
4.学习难点
如何构建一次函数模型.
二、教学设计
(一)课前设计
1.预习任务
任务1:预习教材P102-104页,了解上宽带网有几种收费方式,思考影响收费的因素有哪些?
任务2:思考租车数量由什么决定,租车费用与哪些因素有关?
2.预习自测
1.成渝高铁开通以来,平均运行时速达到300千米/小时,则动车行驶的路程y(千米)与行驶时间x(小时)的函数关系是 .
2.我区的出租车起步价为5元,超过3千米后,每增加1千米加收1.5元,则乘出租车所付费用y(元)与行驶里程x(千米)(x﹥3)的函数关系为 .
3.小明带了100元到商店购买笔记本,已知笔记本的单价是6元一个,则小明剩余的钱y(元)与购买笔记本的数量x(本)的函数关系是 ,小明最多能买 本笔记本.
预习自测: 1. y=300x
2. y=1.5x+0.5
3. y=100-6x,16.
(二)课堂设计
1.知识回顾
(1)形如y=kx+b(k,b是常数且k≠0)的函数,y是x的一次函数.
(2)一次函数y=kx+b中,当k>0时,y随x的增大而增大.当k<0时,y随x的增大而减小.
(3)一元一次方程kx+b=0可看作是直线y=kx+b与x轴交点的横坐标.
(4)一元一次不等式kx+b>0可看作是直线y=kx+b与x轴交点上方图象对应的x的值.
2.问题探究
问题探究一 怎样选取上网收费方式
请认真学习课本P102-103页“问题1”的内容,边学习边思考下列问题:
【知识点:一次函数应用,数学思想:建模思想】
【点拨】
活动一 1.选择方案的依据是什么?
【答】根据省钱原则选择方案
2.要比较三种收费方式的费用,需要做什么?
【答】分别计算每种方案的费用.
3.怎样计算费用?
【答】费用=月使用费+超时费
超时费=超时使用价格 超时使用时间
4.在A,B,C三种上网收费方式中,上网费用是变量的方式有__________,上网费用的多少与__________有关;上网费用是常量的方式是__________.
【答】方案A,B的费用在超过一定时间后,随上网时间变化,是上网时间的函数.
方案C费用固定.
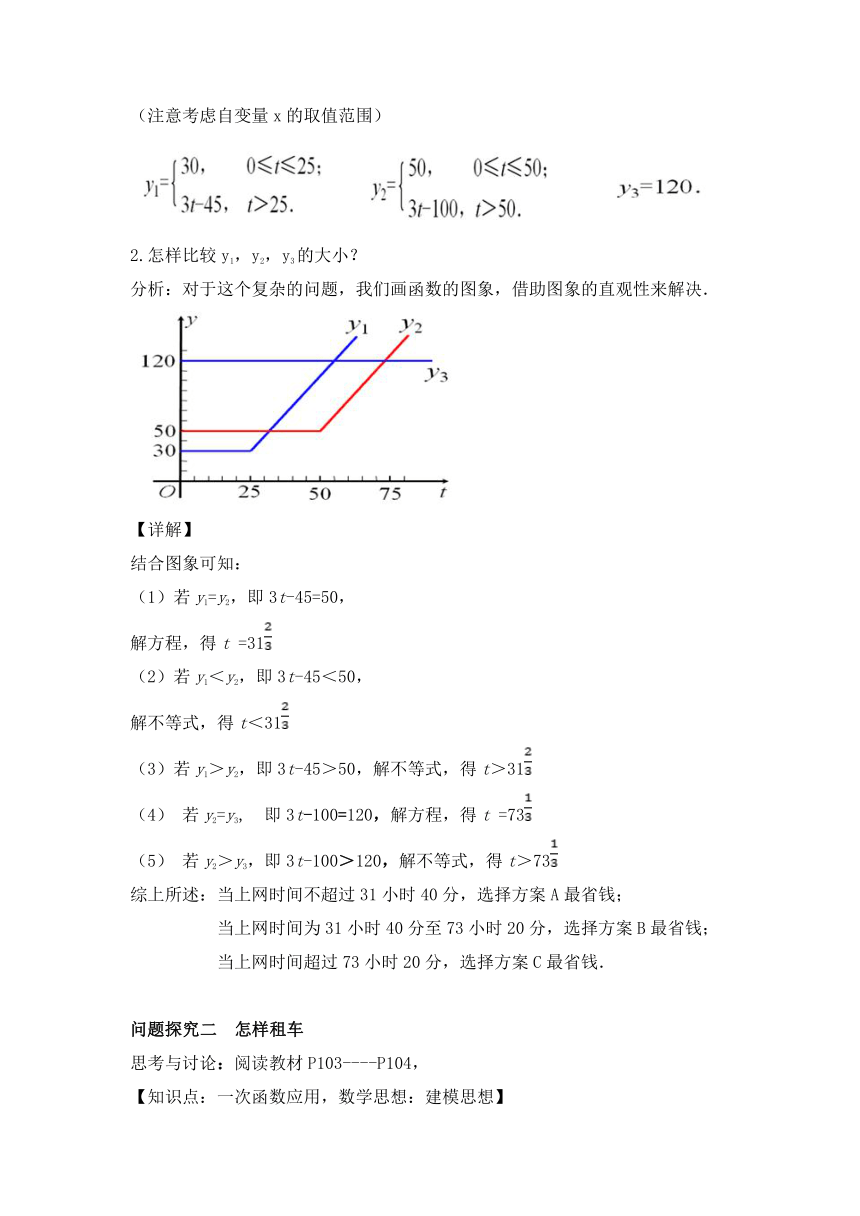
活动二 1.设上网时间为x?h,A,B,C三种方式的收费y1,y2,y3各怎样表示?(注意考虑自变量x的取值范围)
2.怎样比较y1,y2,y3的大小?
分析:对于这个复杂的问题,我们画函数的图象,借助图象的直观性来解决.
【详解】
结合图象可知:
(1)若y1=y2,即3t-45=50,
解方程,得t =31
(2)若y1<y2,即3t-45<50,
解不等式,得t<31
(3)若y1>y2,即3t-45>50,解不等式,得t>31
(4) 若y2=y3, 即3t-100=120,解方程,得t =73
(5) 若y2>y3,即3t-100>120,解不等式,得t>73
综上所述:当上网时间不超过31小时40分,选择方案A最省钱;
当上网时间为31小时40分至73小时20分,选择方案B最省钱;
当上网时间超过73小时20分,选择方案C最省钱.
问题探究二 怎样租车
思考与讨论:阅读教材P103----P104,
【知识点:一次函数应用,数学思想:建模思想】
【点拨】
活动一 1. 影响最后的租车费用的因素有哪些?
【答】主要影响因素是甲,乙两种车所租辆数.
2.汽车所租辆数又与哪些因素有关?
【答】与乘车人数有关.
3.如何由乘车人数确定租车辆数呢?
【答】(1)要保证240 名师生都有车坐,汽车总数不能小于6 辆;
(2)要使每辆汽车上至少有1 名教师,汽车总数不能大于6 辆.
所以共需租6辆车.
活动二 在汽车总数确定后,租车费用与租车的种类有关.如果租甲类车x 辆,能求出租车费用y= .在这个函数中,y随x的增大而 .要求y的最小值,就要先求x的取值范围,怎样求x的取值范围?
【详解】
设租用 x 辆甲种客车,则租用乙种客车的辆数为(6-x)辆;设租车费用为 y,则 y =400x+280(6-x)
化简 得 y =120x+1 680.
(1)为使240 名师生有车坐,则 45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
解得: 4x
据实际意义可取4 或5;因为 y 随着 x 的增大而增大,所以当 x =4 时,y 最小,y 的最小值为2 160. 所以,租甲种车4辆,乙种车2辆.
结论:在涉及多变量的问题的解决中,能合理选择某个变量作为自变量,然后根据问题条件寻求可以反映实际问题的函数.
3.课堂总结
【知识梳理】基础知识思维导图
【重难点突破】(1)本节的问题,其实质是运用一次函数选择最佳方案,一是用一次函数的图像性质;二是多变量的问题.
(2)用一次函数解决生活中的方案选择问题需要根据题意列出函数解析式及图像,分三种情况:函数值相等、大于、小于,结合方程、不等式进行说明,在此基础上选择合理方案.
(3)将实际问题抽象概括成函数模型体现建模思想,其步骤:审清题意---建立数学模型---数学方法解决问题----验证结果.
4.随堂检测
1.为应对雾霾天气,某校决定购买一批口罩,已知超市某种品牌的口罩20元一只,且正打八折促销,则学校买这种口罩x(只)与花钱y(元)的函数关系式为( )
A.y=20x B.y=0.8x C.y=20+0.8x D.y=16x
【知识点:一次函数实际应用,数学思想:建模思想】
【参考答案】D.
【思路点拨】总价=单价×数量×折扣数
2.“五一”小长假期间,张老师驾车从永川到相距300千米外的成都去旅游,已知张老师驾车的平均速度为每小时80千米,在行驶过程中,张老师离成都的距离y(千米)与行驶时间x(小时)的函数关系式为( )
A.y=80x B.y=300-80x C.y=300x D. y=80x+300
【知识点:一次函数实际应用,数学思想:建模思想】
【参考答案】B.
【思路点拨】离成都的路程为余下路程=总路程-走过的路程
3.为大力发展和推广新能源汽车,某小区内新按装了一批电动汽车充电桩,并对小区内的电动汽车充电收费实行包月制,每月收费y(元)与充电时间x(小时)的函数关系如图,其中BA是线段且BA∥x轴,AC是射线.
(1)当 x≥30 时,y 与 x 之间的函数解析式为______________;
(2)若唐老师 4 月份充电 28 小时,他应付________元充电费用;
(3)5月份由于外出旅游,唐老师的充电费用为120元,则他在该月份的充电时间
是 时.
【知识点:一次函数图象信息,数学思想:数形结合,建模思想】
【参考答案】(1).y=3x-30,(2).60,(3).50
【思路点拨】AC段是一次函数图象,用待定系数法可求其解析式.
一、教学目标
1.核心素养: 通过在实际问题中建立函数模型,根据所列函数解析式的性质,选择合理方案解决问题的学习,结合实际问题的数学信息,进行合情推理,提升建立数学模型的能力,发展应用意识.
2.学习目标
(1)巩固一次函数知识,进一步明确一次函数与不等式相结合的实际问题 (?http:?/??/?zk.canpoint.cn?/?" \o "欢迎登陆全品中考网?)处理方法.灵活运用变量之间的关系建立函数模型.
(2)让学生通过“选择上网收费方式”,提高运用函数知识解决实际问题的能力.
(3)让学生通过“怎样租车”,提高运用函数知识解决实际问题的能力.
3.学习重点
(1)培养学生自主分析问题 (?http:?/??/?zk.canpoint.cn?/?" \o "欢迎登陆全品中考网?)的实际背景中包含的变量及对应关系.
(2)运用一次函数的性质解决生活中的最佳方案.
4.学习难点
如何构建一次函数模型.
二、教学设计
(一)课前设计
1.预习任务
任务1:预习教材P102-104页,了解上宽带网有几种收费方式,思考影响收费的因素有哪些?
任务2:思考租车数量由什么决定,租车费用与哪些因素有关?
2.预习自测
1.成渝高铁开通以来,平均运行时速达到300千米/小时,则动车行驶的路程y(千米)与行驶时间x(小时)的函数关系是 .
2.我区的出租车起步价为5元,超过3千米后,每增加1千米加收1.5元,则乘出租车所付费用y(元)与行驶里程x(千米)(x﹥3)的函数关系为 .
3.小明带了100元到商店购买笔记本,已知笔记本的单价是6元一个,则小明剩余的钱y(元)与购买笔记本的数量x(本)的函数关系是 ,小明最多能买 本笔记本.
预习自测: 1. y=300x
2. y=1.5x+0.5
3. y=100-6x,16.
(二)课堂设计
1.知识回顾
(1)形如y=kx+b(k,b是常数且k≠0)的函数,y是x的一次函数.
(2)一次函数y=kx+b中,当k>0时,y随x的增大而增大.当k<0时,y随x的增大而减小.
(3)一元一次方程kx+b=0可看作是直线y=kx+b与x轴交点的横坐标.
(4)一元一次不等式kx+b>0可看作是直线y=kx+b与x轴交点上方图象对应的x的值.
2.问题探究
问题探究一 怎样选取上网收费方式
请认真学习课本P102-103页“问题1”的内容,边学习边思考下列问题:
【知识点:一次函数应用,数学思想:建模思想】
【点拨】
活动一 1.选择方案的依据是什么?
【答】根据省钱原则选择方案
2.要比较三种收费方式的费用,需要做什么?
【答】分别计算每种方案的费用.
3.怎样计算费用?
【答】费用=月使用费+超时费
超时费=超时使用价格 超时使用时间
4.在A,B,C三种上网收费方式中,上网费用是变量的方式有__________,上网费用的多少与__________有关;上网费用是常量的方式是__________.
【答】方案A,B的费用在超过一定时间后,随上网时间变化,是上网时间的函数.
方案C费用固定.
活动二 1.设上网时间为x?h,A,B,C三种方式的收费y1,y2,y3各怎样表示?(注意考虑自变量x的取值范围)
2.怎样比较y1,y2,y3的大小?
分析:对于这个复杂的问题,我们画函数的图象,借助图象的直观性来解决.
【详解】
结合图象可知:
(1)若y1=y2,即3t-45=50,
解方程,得t =31
(2)若y1<y2,即3t-45<50,
解不等式,得t<31
(3)若y1>y2,即3t-45>50,解不等式,得t>31
(4) 若y2=y3, 即3t-100=120,解方程,得t =73
(5) 若y2>y3,即3t-100>120,解不等式,得t>73
综上所述:当上网时间不超过31小时40分,选择方案A最省钱;
当上网时间为31小时40分至73小时20分,选择方案B最省钱;
当上网时间超过73小时20分,选择方案C最省钱.
问题探究二 怎样租车
思考与讨论:阅读教材P103----P104,
【知识点:一次函数应用,数学思想:建模思想】
【点拨】
活动一 1. 影响最后的租车费用的因素有哪些?
【答】主要影响因素是甲,乙两种车所租辆数.
2.汽车所租辆数又与哪些因素有关?
【答】与乘车人数有关.
3.如何由乘车人数确定租车辆数呢?
【答】(1)要保证240 名师生都有车坐,汽车总数不能小于6 辆;
(2)要使每辆汽车上至少有1 名教师,汽车总数不能大于6 辆.
所以共需租6辆车.
活动二 在汽车总数确定后,租车费用与租车的种类有关.如果租甲类车x 辆,能求出租车费用y= .在这个函数中,y随x的增大而 .要求y的最小值,就要先求x的取值范围,怎样求x的取值范围?
【详解】
设租用 x 辆甲种客车,则租用乙种客车的辆数为(6-x)辆;设租车费用为 y,则 y =400x+280(6-x)
化简 得 y =120x+1 680.
(1)为使240 名师生有车坐,则 45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
解得: 4x
据实际意义可取4 或5;因为 y 随着 x 的增大而增大,所以当 x =4 时,y 最小,y 的最小值为2 160. 所以,租甲种车4辆,乙种车2辆.
结论:在涉及多变量的问题的解决中,能合理选择某个变量作为自变量,然后根据问题条件寻求可以反映实际问题的函数.
3.课堂总结
【知识梳理】基础知识思维导图
【重难点突破】(1)本节的问题,其实质是运用一次函数选择最佳方案,一是用一次函数的图像性质;二是多变量的问题.
(2)用一次函数解决生活中的方案选择问题需要根据题意列出函数解析式及图像,分三种情况:函数值相等、大于、小于,结合方程、不等式进行说明,在此基础上选择合理方案.
(3)将实际问题抽象概括成函数模型体现建模思想,其步骤:审清题意---建立数学模型---数学方法解决问题----验证结果.
4.随堂检测
1.为应对雾霾天气,某校决定购买一批口罩,已知超市某种品牌的口罩20元一只,且正打八折促销,则学校买这种口罩x(只)与花钱y(元)的函数关系式为( )
A.y=20x B.y=0.8x C.y=20+0.8x D.y=16x
【知识点:一次函数实际应用,数学思想:建模思想】
【参考答案】D.
【思路点拨】总价=单价×数量×折扣数
2.“五一”小长假期间,张老师驾车从永川到相距300千米外的成都去旅游,已知张老师驾车的平均速度为每小时80千米,在行驶过程中,张老师离成都的距离y(千米)与行驶时间x(小时)的函数关系式为( )
A.y=80x B.y=300-80x C.y=300x D. y=80x+300
【知识点:一次函数实际应用,数学思想:建模思想】
【参考答案】B.
【思路点拨】离成都的路程为余下路程=总路程-走过的路程
3.为大力发展和推广新能源汽车,某小区内新按装了一批电动汽车充电桩,并对小区内的电动汽车充电收费实行包月制,每月收费y(元)与充电时间x(小时)的函数关系如图,其中BA是线段且BA∥x轴,AC是射线.
(1)当 x≥30 时,y 与 x 之间的函数解析式为______________;
(2)若唐老师 4 月份充电 28 小时,他应付________元充电费用;
(3)5月份由于外出旅游,唐老师的充电费用为120元,则他在该月份的充电时间
是 时.
【知识点:一次函数图象信息,数学思想:数形结合,建模思想】
【参考答案】(1).y=3x-30,(2).60,(3).50
【思路点拨】AC段是一次函数图象,用待定系数法可求其解析式.
