第4节 探索三角形相似的条件（4课时）

课件22张PPT。第4节 探索三角形相似的条件（1）北师大版 九年级上 第30课时精题导练如图所示，在△ABC中，AB＝AC，BD＝CD，CE⊥AB于E，求证：△ABD∽△CBE．【答案】∵AB＝AC，BD＝CD，CE⊥AB，
∴∠ADB＝∠CEB＝90°，
又∠B＝∠B，
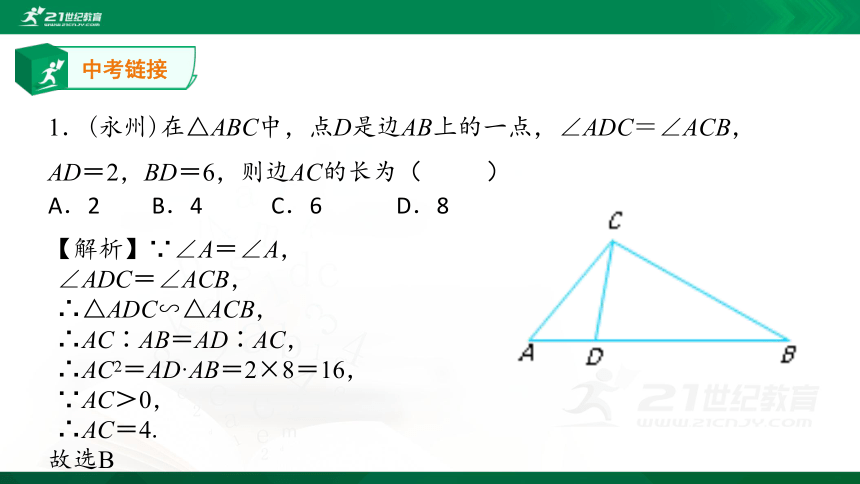
∴△ABD∽∠CBE．中考链接1．(永州)在△ABC中，点D是边AB上的一点，∠ADC＝∠ACB，AD＝2，BD＝6，则边AC的长为（ ）
A．2 B．4 C．6 D．8【解析】∵∠A＝∠A，
∠ADC＝∠ACB，
∴△ADC∽△ACB，
∴AC∶AB＝AD∶AC，
∴AC2＝AD·AB＝2×8＝16，
∵AC＞0，
∴AC＝4.
故选B中考链接2．(包头)如图所示，已知AB∥CD，若 = ，则 = .【解析】∵AB∥CD，
∴△OAB∽△OCD，
∴
故答案为：第4节 探索三角形相似的条件（1）北师大版 九年级上 第31课时精题导练如图所示，在正方形ABCD中，P是BC上的一点，且BP＝3PC，Q是CD的中点，连接AP．
（1）求证：△ADQ∽△QCP；
（2）求证：AQ⊥PQ.【答案】（1）∵四边形ABCD是正方形，
∴AD＝CD＝BC，∠C＝∠D＝90°．
∵BP＝3PC,∴CP＝精题导练又∵Q是CD的中点，
∴CQ＝DQ＝ CD.
∴ ，
∴
又∵∠C＝∠D，
∴△ADQ∽△QCP精题导练（2）∵△ADQ∽△QCP，
∴∠PQC＝∠QAD．
∵∠QAD＋∠AQD＝90°，
得到∠PQC＋∠AQD＝90°．
∴∠AQP＝90°，
即AQ⊥PQ．中考链接(宿迁)在三角形ABC中，AB＝AC，点E在边BC上移动(点E不与点B，C重合)，满足∠DEF＝∠B，且点D，F分别在边AB，AC上．
（1）求证：△BDE∽△CEF；
（2）当点E 移动到BC的中点时，求证：FE平分∠DFC.【答案】（1）∵AB＝AC，
∴∠B＝∠C．
∵∠BDE＝180°－∠B－∠DEB，
∠CEF＝180°－∠DEF－∠DEB，
∵∠DEF＝∠B，
∴∠BDE＝∠CEF，
∴△BDE∽△CEF．中考链接（2）∵△BDE∽△CEF，
∴
∵点E是BC的中点，
∴BE＝CE．
∴
∵∠DEF＝∠B＝∠C，∴△DEF∽△CEF．
∴∠DFE＝∠CFE．∴FE平分∠DFC．第4节 探索三角形相似的条件（1）北师大版 九年级上 第32课时精题导练如图所示，在□ABCD中，对角线AC，BD相交于点O，点E，F是AD上的点，且AE＝EF＝FD．连接BE，BF，分别交AO于点G，H．
（1）求EG∶BG的值；
（2）求证：AG＝OG.【答案】（1）∵四边形ABCD是平行四边形，
∴AO＝ AC，AD＝BC,AD∥BC．
∴△AEG∽△CBG．
精题导练∵AE＝EF＝FD，
∴BC＝AD＝2AE．
GC＝3AG，GB＝3EG．
∴EG∶BG＝1∶3．
（2）∵GC＝3AG（已证），
∴AC＝4AG，
∴AO＝ AC＝2AG．
∴GO＝AO－AG＝AG．中考链接(丽水)如图所示，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上．
（1）判断△ABC和△DEF是否相似，并说明理由；
（2）P1，P2，P3，P4，P5，D，F是△DEF边上的7个格点，请在这7个格点中选取3个点作为三角形的顶点，使构成的三角形与△ABC相似（要求写出2个符合条件的三角形，并在图中连结相应的线段，不必说明理由）．
中考链接【答案】（1）△ABC和△DEF相似．
根据勾股定理，得AB＝2 ，AC= ，BC=5，
DE=4 ，DF=2 ，EF=2 .
∵ ，∴△ABC∽△DEF．
（2）答案不唯一，下面6个三角形中的任意2个均可．
△P2P5D，△P4P5F，△P2P4D，△P4P5D，△P2P4P5，△P1FD．第4节 探索三角形相似的条件（1）北师大版 九年级上 第33课时精题导练一个舞台长12 m，当主持人站在该舞台的黄金分割点处时，音响效果才最佳，请你帮主持人计算一下他应站在舞台的什么位置．【答案】如图所示，用线段AB表示该舞台，P,Q是线段AB的两个黄金分割点.
∵主持人站在黄金分割点处，
∴ 或精题导练又∵AB＝12 m，
∴AQ＝6（ ）或BP＝6（ ）m.
答：主持人应站在距A点6（ ）m处或距B点6（ ） m处.中考链接(六盘水)矩形的两边长分别为a，b，下列数据能构成黄金矩形的是（ ）．
A．a＝4，b＝ ＋2
B．a＝4，b＝ －2
C．a＝2，b＝ ＋1
D．a＝2，b＝ －1中考链接【解析】∵宽与长的比是 的矩形叫做黄金矩形，

∴a＝2，b＝ -1
故选D．
谢谢21世纪教育网（www.21cnjy.com) 中小学教育资源网站 有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php