第7节 相似三角形的性质（2课时）

课件13张PPT。第7节 相似三角形的性质（1）北师大版 九年级上 第36课时精题导练1．若△ABC∽△DEF，且AB＝2DE，h1，h2分别为AB，DE边上的高线，则 = . 【解析】∵△ABC∽△DEF，
h1，h2分别为AB，DE边上的高线，
∴
∵AB＝2DE，
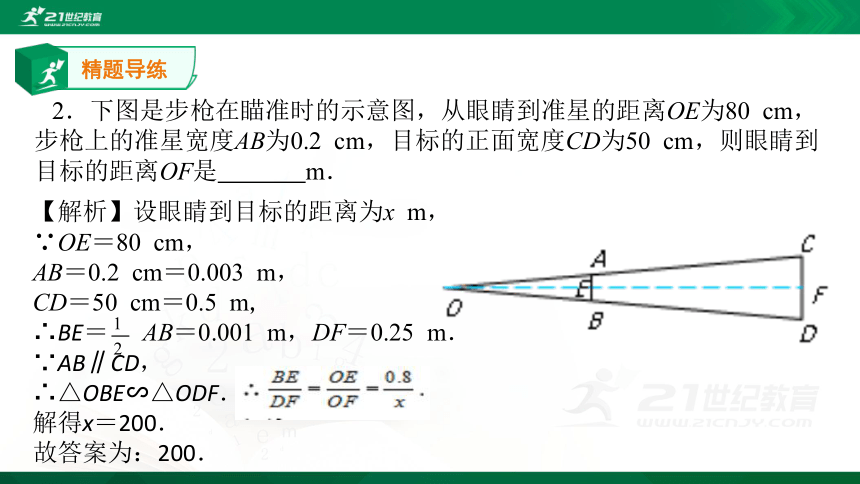
∴ =2.精题导练2．下图是步枪在瞄准时的示意图，从眼睛到准星的距离OE为80 cm，步枪上的准星宽度AB为0.2 cm，目标的正面宽度CD为50 cm，则眼睛到目标的距离OF是 m．【解析】设眼睛到目标的距离为x m，
∵OE＝80 cm，
AB＝0.2 cm＝0.003 m，
CD＝50 cm＝0.5 m,
∴BE＝ AB＝0.001 m，DF＝0.25 m．
∵AB∥CD，
∴△OBE∽△ODF．
解得x＝200．
故答案为：200． 中考链接1．(重庆)若△ABC∽△DEF，相似比为3∶2，则对应高的比为（ ）
A．3∶2 B．3∶5
C．9∶4 D．4∶9【答案】∵△ABC∽△DEF，相似比为3∶2，
∴对应高的比为：3∶2．
故选：A．中考链接2.(绍兴)学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO＝4 m，AB＝1.6 m，CO＝1 m，则栏杆C端应下降的垂直距离CD为（ ）
A．0.2 m B．0.3 m C．0.4 m D．0.5 m课堂练习【解析】由题意知，△ABO∽△CDO，
根据相似三角形的性质可得
，AO＝4 m，
AB＝1.6 m，CO＝1 m,
CD＝1×1÷4＝0.4，
故选C.第7节 相似三角形的性质（1）北师大版 九年级上 第37课时精题导练如图所示，在△ABC中， ， ∠BAD＝∠CAE，△ABC的周长是12 cm,△ADE面积是135 cm2．
（1）求△ADE的周长；
（2）△ABC的面积． 【答案】（1）∵∠ADB＝∠CAE，
∴∠ADB＋∠CAD＝∠CAE＋∠CAD，
即∠BAC＝∠DAE．
又∵精题导练∴△ABC∽△ADE．
∵ ，
△ABC的周长是12 cm,
∴△ADE的周长为 =18cm
中考链接(德阳)如图所示，四边形ABCD为菱形，M为BC上一点，连接AM交对角线BD于点G，并且∠ABM＝2∠BAM．
（1）求证：AG＝BG；
（2）若点M为BC的中点，同时S△BMG＝1，求△ADG的面积．【答案】（1）∵四边形ABCD是菱形，
∴∠ABD＝∠CBD，
∵∠ABM＝2∠BAM，
∴∠ABD＝∠BAM．
∴AG＝BG．中考链接（2）∵AD∥BC，
∴△ADG∽△MBG，
∴
∵点M为BC的中点，谢谢21世纪教育网（www.21cnjy.com) 中小学教育资源网站 有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php