人教高中数学 (A版)必修四 2.4.1 平面向量数量积的含义 课件(共30张PPT)
文档属性
| 名称 | 人教高中数学 (A版)必修四 2.4.1 平面向量数量积的含义 课件(共30张PPT) | 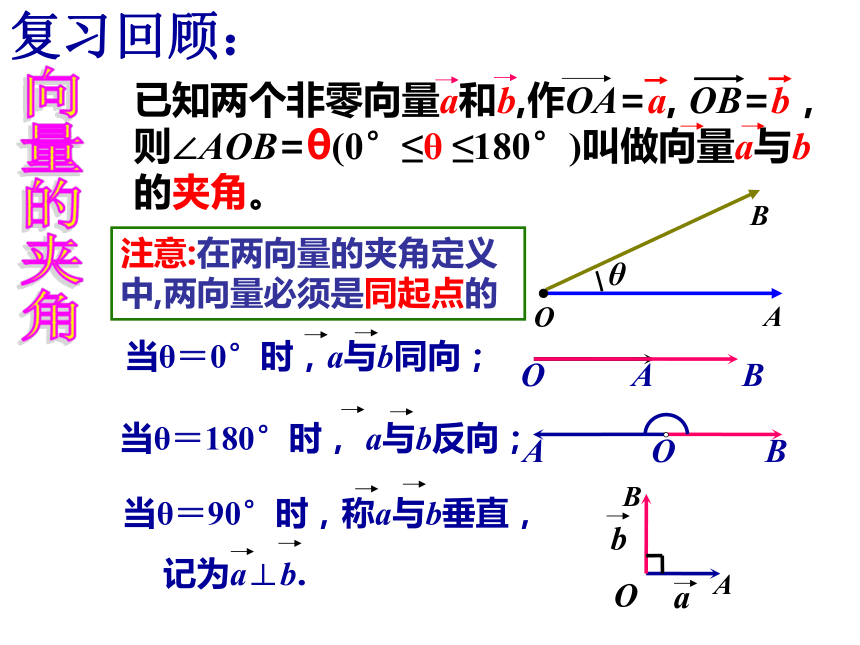 | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-05 11:52:33 | ||
图片预览











文档简介
课件30张PPT。OBAθ向量的夹角复习回顾:注意:在两向量的夹角定义中,两向量必须是同起点的练习:(1)(2)(3) 任意两个向量都可以进行加,减运算,同时两个向量的和与差仍是一个向量,并且向量的加法运算满足交换律和结合律.由于任意两个实数可以进行乘法运算,我们自然会提出,任意两个向量是否也可以进行乘法运算呢?对此,我们从理论上进行相应分析. 引入:新课引入: 我们学过功的概念,即一个物体在力F的作用下产生位移S(如图)其中θ是F与S的夹角,那么力F所做的功W,可以用如下式子计算:
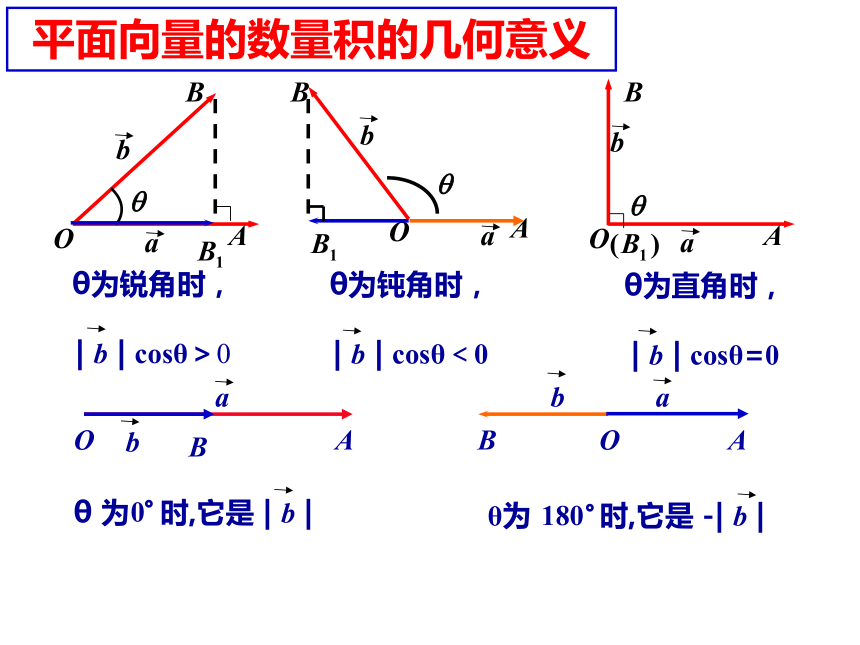
平面向量的数量积定义注意:向量的数量积是一个数量。 (2)两向量的数量积是一个数量,而不是向量,符号由夹角决定;定义理解:思考:你会变吗?会用吗?试试看平面向量的数量积的几何意义平面向量的数量积的几何意义是:平面向量的数量积的几何意义重要性质:特别地我真的理解了吗?真假 假 假 真假 假真进行向量数量积计算时,既要考虑向量的模,又要根据两个向量方向确定其夹角4钝角三角形?25练习一:3练习一:A4.数量积的运算律:⑴交换律:⑵数乘的结合律:⑶分配律:注意:数量积不满足结合律即即-72600注意:两个向量的数量积是否为零,
是判断相应的两条直线是否垂直的重
要方法之一.练习二:CC练习二:等边三角形D( )CA. 重心、外心、垂心 B. 重心、外心、内心
C. 外心、重心、垂心 D. 外心、重心、内心思考:重要结论:小结: 本节课我们主要学习了平面向量数量积性质的应用,常见的题型主要有:1、直接计算数量积(定义式以及夹角的定义)2、由数量积求向量的模4、运用数量积的性质判定两向量是否垂直3、由数量积确定两向量的夹角5、判断三角形的形状
平面向量的数量积定义注意:向量的数量积是一个数量。 (2)两向量的数量积是一个数量,而不是向量,符号由夹角决定;定义理解:思考:你会变吗?会用吗?试试看平面向量的数量积的几何意义平面向量的数量积的几何意义是:平面向量的数量积的几何意义重要性质:特别地我真的理解了吗?真假 假 假 真假 假真进行向量数量积计算时,既要考虑向量的模,又要根据两个向量方向确定其夹角4钝角三角形?25练习一:3练习一:A4.数量积的运算律:⑴交换律:⑵数乘的结合律:⑶分配律:注意:数量积不满足结合律即即-72600注意:两个向量的数量积是否为零,
是判断相应的两条直线是否垂直的重
要方法之一.练习二:CC练习二:等边三角形D( )CA. 重心、外心、垂心 B. 重心、外心、内心
C. 外心、重心、垂心 D. 外心、重心、内心思考:重要结论:小结: 本节课我们主要学习了平面向量数量积性质的应用,常见的题型主要有:1、直接计算数量积(定义式以及夹角的定义)2、由数量积求向量的模4、运用数量积的性质判定两向量是否垂直3、由数量积确定两向量的夹角5、判断三角形的形状
