人教版数学七年级下册 8.1.1二元一次方程组课件(20张ppt)
文档属性
| 名称 | 人教版数学七年级下册 8.1.1二元一次方程组课件(20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-06 14:11:47 | ||
图片预览







文档简介
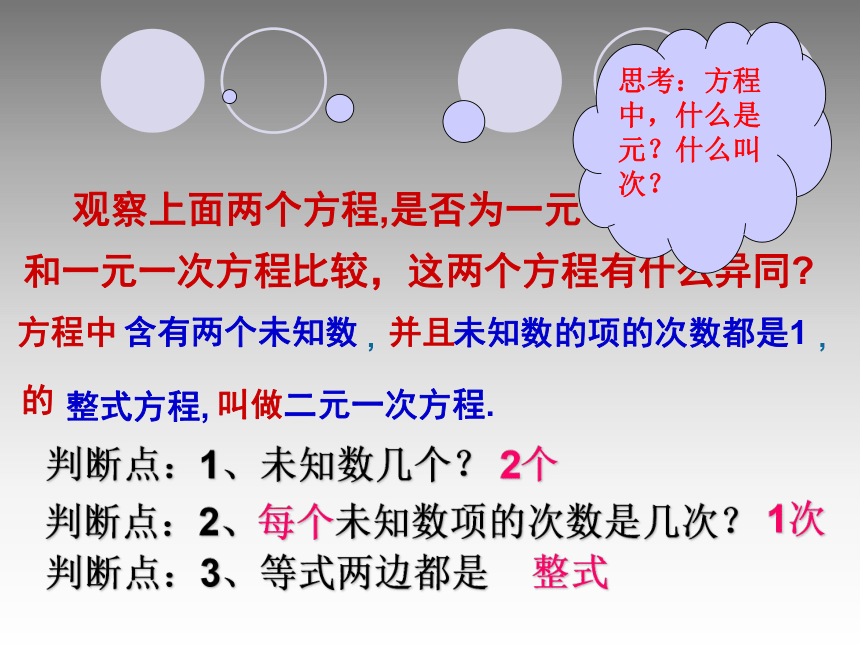
课件20张PPT。问题: 篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部5场比赛中得到7分,那么这个队胜负场数分别是多少?解法一:一元一次方程等量关系:胜场积分+负场积分=总积分???答:胜了2场,负了3场。问题: 篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部5场比赛中得到7分,那么这个队胜负场数分别是多少?等量关系:胜的场数+负的场数=总场数胜场积分+负场积分=总积分解:设该队胜了x场,负了y场
????观察上面两个方程,是否为一元一次方程?和一元一次方程比较,有什么异同?8.1 二元一次方程组观察上面两个方程,是否为一元一次方程?和一元一次方程比较,这两个方程有什么异同?含有两个未知数未知数的项的次数都是1方程中并且的,,判断点:1、未知数几个?判断点:2、每个未知数项的次数是几次?判断点:3、等式两边都是2个1次整式整式方程,叫做二元一次方程.思考:方程中,什么是元?什么叫次?判断点:1、未知数几个?判断点:2、每个未知数的项的最高次数是几次?判断点:3、等式两边是2个1次整式??????下列哪些是二元一次方程?是不是不是不是不是不是不是?试一试:解:由已知得:
a-2≠0 |a|-1=1
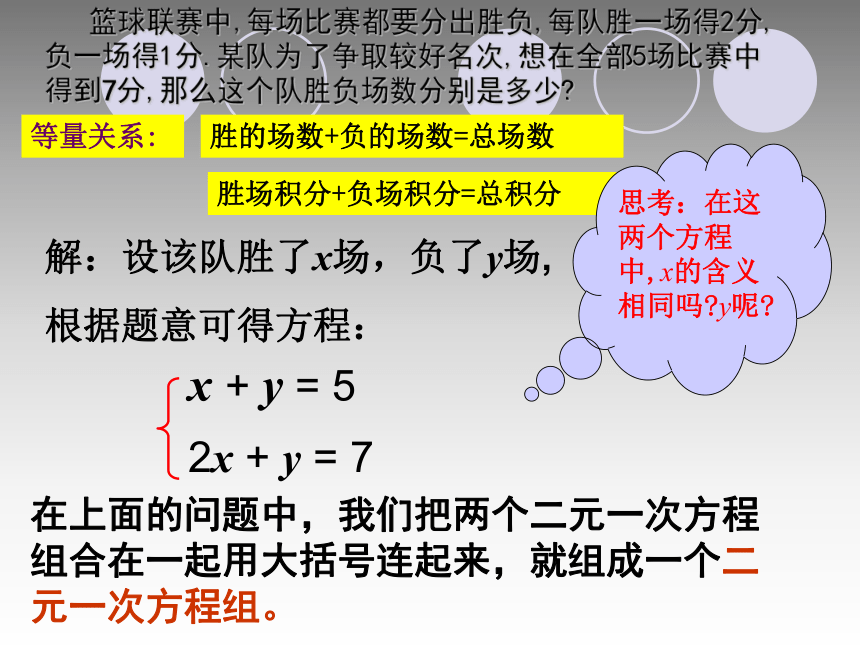
∴ a=-2x + y = 5在上面的问题中,我们把两个二元一次方程组合在一起用大括号连起来,就组成一个二元一次方程组。 篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部5场比赛中得到7分,那么这个队胜负场数分别是多少?等量关系:胜的场数+负的场数=总场数胜场积分+负场积分=总积分解:设该队胜了x场,负了y场,
根据题意可得方程:思考:在这两个方程中,x的含义相同吗?y呢?2x + y = 7?通过上面的问题,你认为判断一组方程是否为二元一次方程组要满足哪些条件?(是)(不是)(不是)(不是)(是)(不是)①方程组中一共有2个不同未知数;
②方程组有2个一次整式方程组成;
③一般用大括号把2个方程连起来。请你说说二元一次方程组有哪些特点?(互相讨论一下)方程组中有两个未知数,含有未知数的项的次数是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.探究: 2.再找出方程2x + y = 7的符合实际意义的解,并用表格罗列. 使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的一个解.记作注意:二元一次方程的解有无数个。y05123413245 0y = 5 71 35x = 0x = y =那么方程组
2x + y = 7
x + y = 5
的解是??
?xxy05123413245 0 71 35x = 0y = 5x = 1y = 4x = 2y = 3x = 3y = 2x = 4y =1x = 5y = 0x = 0y = 7x = 1y = 5x = 2y = 3x = 3y = 1 二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2x = 2y = 3y = 3xy05123413245 0x = 2y = 3x = 2y = 3x = 2x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2x = 2x = 2y = 3x = 2x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2所以, x = 2
y = 3
是 2x + y = 7
x + y = 5
的公共解。
练一练:1.填表:使每对x,y的值是方程3x+y=5的解.
2.已知下列三对数值
________是方程x+y=7的解;
________是方程2x+y=9的解,
_______是方程组 的解. 1153.8-11.82 1x=2
y=5x=1
y=7x + y=7
2x+y=91.5x=1
y=6考考你:给你一对数值x = 2
y = 5⑴ 你能写出一个二元一次方程,使这对数值是满足这个方程的一个解吗?⑵ 你能写出一个二元一次方程组,使这对数值是满足这个方程组的解吗??思考2GO4?B4、方程组的解是( )A. B.C. D.C一、方程中含有两个未知数(x和y),并且
含有未知数的项的次数都是1,像这样的方程
叫做二元一次方程。
课堂小结:二、把两个一次方程合在一起后共有两个未知数,就组成了一个二元一次方程组。
三、使二元一次方程两边的值相等的两
个未知数的值,叫做二元一次方程的解。四、一般地,二元一次方程组的两个方
程的公共解,叫做二元一次方程组的解。
五、二元一次方程有无数多个解;二元一次方程组有且只有一组解。
这节课你有哪些收获给大家分享一下!
“鸡兔同笼”问题出自我国古代数学名著《孙子算经》。书中的题目是这样的:“今有鸡兔同笼,上有五头,下有十六足,问鸡兔各几何?”你知道吗?解:设有鸡x只,兔y只,根据题意列方程组得:
x + y = 5
2x + y = 16
鸡兔同笼1. 用表格罗列二元一次方程2x + y = 10的所有正整数解.
2. P90 习题8.1第3、第5题。作业布置一、大作业
????观察上面两个方程,是否为一元一次方程?和一元一次方程比较,有什么异同?8.1 二元一次方程组观察上面两个方程,是否为一元一次方程?和一元一次方程比较,这两个方程有什么异同?含有两个未知数未知数的项的次数都是1方程中并且的,,判断点:1、未知数几个?判断点:2、每个未知数项的次数是几次?判断点:3、等式两边都是2个1次整式整式方程,叫做二元一次方程.思考:方程中,什么是元?什么叫次?判断点:1、未知数几个?判断点:2、每个未知数的项的最高次数是几次?判断点:3、等式两边是2个1次整式??????下列哪些是二元一次方程?是不是不是不是不是不是不是?试一试:解:由已知得:
a-2≠0 |a|-1=1
∴ a=-2x + y = 5在上面的问题中,我们把两个二元一次方程组合在一起用大括号连起来,就组成一个二元一次方程组。 篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部5场比赛中得到7分,那么这个队胜负场数分别是多少?等量关系:胜的场数+负的场数=总场数胜场积分+负场积分=总积分解:设该队胜了x场,负了y场,
根据题意可得方程:思考:在这两个方程中,x的含义相同吗?y呢?2x + y = 7?通过上面的问题,你认为判断一组方程是否为二元一次方程组要满足哪些条件?(是)(不是)(不是)(不是)(是)(不是)①方程组中一共有2个不同未知数;
②方程组有2个一次整式方程组成;
③一般用大括号把2个方程连起来。请你说说二元一次方程组有哪些特点?(互相讨论一下)方程组中有两个未知数,含有未知数的项的次数是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.探究: 2.再找出方程2x + y = 7的符合实际意义的解,并用表格罗列. 使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的一个解.记作注意:二元一次方程的解有无数个。y05123413245 0y = 5 71 35x = 0x = y =那么方程组
2x + y = 7
x + y = 5
的解是??
?xxy05123413245 0 71 35x = 0y = 5x = 1y = 4x = 2y = 3x = 3y = 2x = 4y =1x = 5y = 0x = 0y = 7x = 1y = 5x = 2y = 3x = 3y = 1 二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2x = 2y = 3y = 3xy05123413245 0x = 2y = 3x = 2y = 3x = 2x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2x = 2x = 2y = 3x = 2x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3x = 2y = 3y = 3x = 2x = 2y = 3y = 3x = 2所以, x = 2
y = 3
是 2x + y = 7
x + y = 5
的公共解。
练一练:1.填表:使每对x,y的值是方程3x+y=5的解.
2.已知下列三对数值
________是方程x+y=7的解;
________是方程2x+y=9的解,
_______是方程组 的解. 1153.8-11.82 1x=2
y=5x=1
y=7x + y=7
2x+y=91.5x=1
y=6考考你:给你一对数值x = 2
y = 5⑴ 你能写出一个二元一次方程,使这对数值是满足这个方程的一个解吗?⑵ 你能写出一个二元一次方程组,使这对数值是满足这个方程组的解吗??思考2GO4?B4、方程组的解是( )A. B.C. D.C一、方程中含有两个未知数(x和y),并且
含有未知数的项的次数都是1,像这样的方程
叫做二元一次方程。
课堂小结:二、把两个一次方程合在一起后共有两个未知数,就组成了一个二元一次方程组。
三、使二元一次方程两边的值相等的两
个未知数的值,叫做二元一次方程的解。四、一般地,二元一次方程组的两个方
程的公共解,叫做二元一次方程组的解。
五、二元一次方程有无数多个解;二元一次方程组有且只有一组解。
这节课你有哪些收获给大家分享一下!
“鸡兔同笼”问题出自我国古代数学名著《孙子算经》。书中的题目是这样的:“今有鸡兔同笼,上有五头,下有十六足,问鸡兔各几何?”你知道吗?解:设有鸡x只,兔y只,根据题意列方程组得:
x + y = 5
2x + y = 16
鸡兔同笼1. 用表格罗列二元一次方程2x + y = 10的所有正整数解.
2. P90 习题8.1第3、第5题。作业布置一、大作业
