第三章 圆复习学案(含答案)
图片预览



文档简介
第三章 圆
1.解决与弦有关的问题
垂径定理和勾股定理有机结合计算弦长、半径、圆心到弦的距离等问题的方法——构造直角三角形;在圆中解决与弦有关问题经常作的辅助线——圆心到弦的距离.
【例】如图,平面直角坐标系中,☉P与x轴分别交于A,B两点,点P的坐标为(3,-1),AB=2.
(1)求☉P的半径.
(2)将☉P向下平移,求☉P与x轴相切时平移的距离.
【标准解答】(1)作PC⊥AB于C,连接PA.∴AC=CB=AB.
∵AB=2,∴AC=.
∵点P的坐标为(3,-1),∴PC=1.
在Rt△PAC中,∠PCA=90°,
∴PA===2.
∴☉P的半径为2.
(2)将☉P向下平移,☉P与x轴相切时平移的距离为2-1=1.
1.如图,☉O的直径CD=5cm,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OD=3∶5.则AB的长是 ( )
A.2 cm B.3 cm
C.4 cm D.2cm
1题图
2题图
2.如图☉O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为
( )
A.2 B.4 C.4 D.8
3.☉O过点B,C,圆心O在等腰直角△ABC内部,∠BAC=90°,OA=1,BC=6,则☉O的半径为 ( )
A. B.2
C. D.3
2.与圆心角、圆周角有关的问题
(1)利用圆周角定理将圆心角与圆周角进行转化.
(2)利用同弧所对的圆周角相等进行角与角的转化.
(3)利用直径所对的圆周角是直角构造直角三角形,为勾股定理、解直角三角形等知识的应用创造条件.
(4)利用圆内接四边形的性质求圆心角或圆周角.
【例1】如图,☉O中,弦AB,CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于
( )
A.30° B.35° C.40° D.50°
【标准解答】选C.∵∠APD是△APC的外角,∴∠APD=∠C+∠A;
∵∠A=30°,∠APD=70°,
∴∠C=∠APD-∠A=40°.
∴∠B=∠C=40°.
【例2】如图,将三角板的直角顶点放在☉O的圆心上,两条直角边分别交☉O于A,B两点,点P在优弧AB上,且与点A,B不重合,连接PA,PB,则∠APB的大小为 度.
【标准解答】∵∠AOB与∠APB为所对的圆心角和圆周角,
∴∠APB=∠AOB=×90°=45°.
答案:45
【例3】如图,☉O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是 .
【标准解答】连接AD,
∵CD是直径,
∴∠CAD=90°,
∵∠B=40°,
∴∠D=40°,
∴∠ACD=50°.
答案:50°
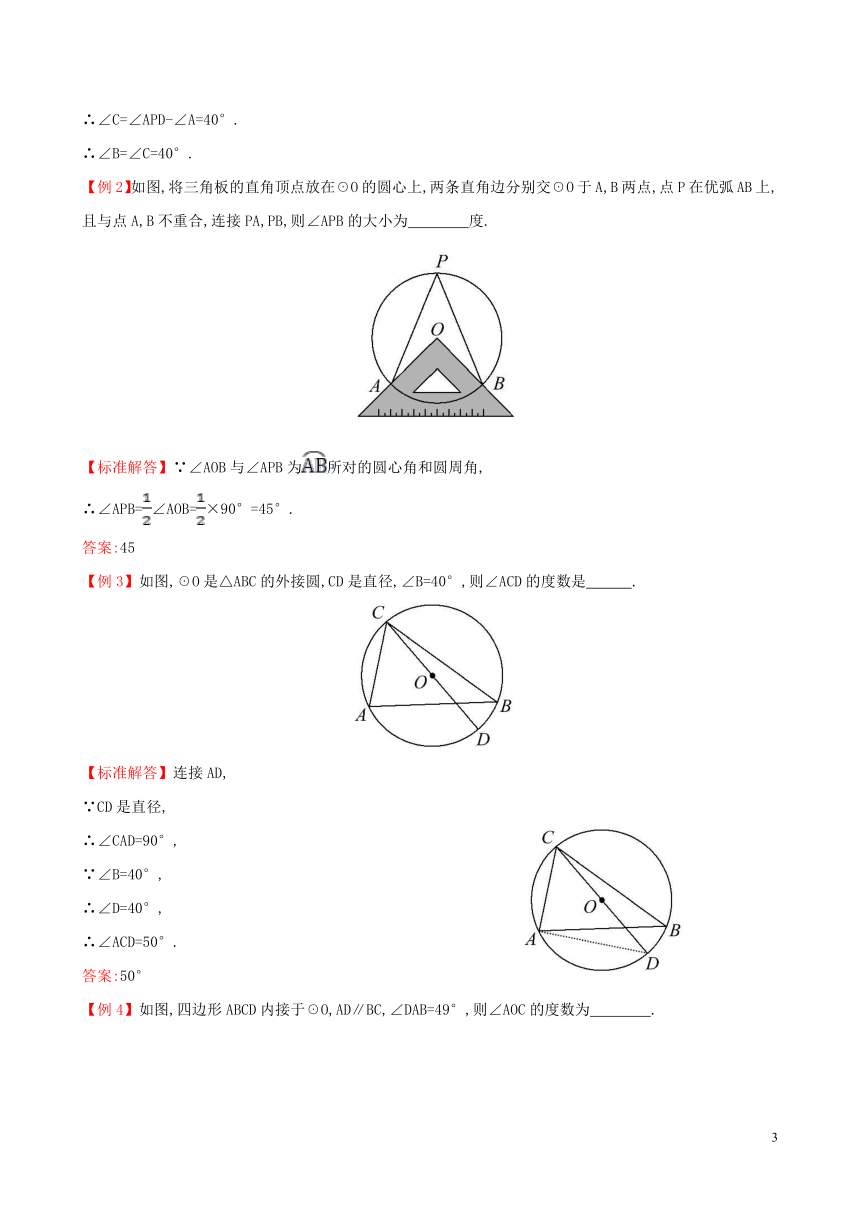
【例4】如图,四边形ABCD内接于☉O,AD∥BC,∠DAB=49°,则∠AOC的度数为 .
【标准解答】如图,在上取点M,连接AM,CM,
∵AD∥BC,∠DAB=49°,
∴∠ABC=131°,
∴∠M=49°,
∠AOC=98°.
答案:98°
1.如图,☉O的直径CD⊥AB,∠AOC=50°,则∠CDB的大小为 ( )
A.25° B.30° C.40° D.50°
1题图
2题图
3题图
2.如图,AB是☉O的直径,C,D,E都是☉O上的点,则∠ACE+∠BDE= ( )
A.60° B.75° C.90° D.120°
3.如图,在☉O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E= °.
4.如图,AB是☉O的直径,C是弧AE的中点,CD⊥AB于D,交AE于F,连接AC,试证明AF=CF.
3.切线的判定与性质
(1)切线的三种判定方法
①从公共点的个数来判断:直线与圆有且只有一个公共点;
②从圆心到直线的距离来判断:圆心到直线的距离等于圆的半径;
③应用判定定理:经过半径外端且与半径垂直.
(2)利用切线的判定定理的两个思路
①连半径,证垂直:
若已知直线与圆有公共点,则连接圆心和公共点,证明垂直.
②作垂线,证等径:
若直线与圆的公共点没有确定,则过圆心作直线的垂线,证明圆心到直线的距离等于半径.
(3)切线性质应用的两个思路
①有切点:连接切点和半径,必垂直,建直角三角形;
②无切点:过圆心作半径,必垂直,得切点,建直角三角形.
【例1】如图,在△ABC中,∠C=90°①,∠ABC的平分线交AC于点E②,过点E作BE的垂线于点F③,☉O是△BEF的外接圆.
(1)求证:AC是☉O的切线④.
(2)过点E作EH⊥AB于点H⑤,
求证:CD=HF.
【信息解读·破译解题秘钥】
条件②直译为:∠CBE=∠FBE⑥.
条件③翻译为:BF为圆O的直径.
破译:连接OE,则可得∠OBE=∠OEB,整合条件②③,可得OE∥BC⑦.
破译:整合条件①⑥⑦得到OE⊥AC,进而得到AC是☉O的切线.
条件②翻译为:=,进而得到DE=EF⑧.
破译:整合条件①②⑤,得到CE=EH⑨.
破译:整合条件①⑤⑧⑨,得到△ECD≌△EHF,进而得到CD=HF.
【标准解答】(1)连接OE.
∵BE⊥EF,
∴∠BEF=90°,
∴BF为☉O的直径.
∵BE平分∠ABC,
∴∠OBE=∠CBE.
∵OB=OE,∴∠OBE=∠OEB.
∴∠CBE=∠OEB.∴OE∥BC.
∴∠OEA=∠C=90°.∴OE⊥AC.
∴AC是☉O的切线.
(2)连接DE.
∵∠OBE=∠CBE,∴=.
∴DE=EF.
∵BE平分∠ABC,EC⊥BC,EH⊥AB,
∴EC=EH.
又∵∠C=∠EHF=90°,DE=EF,
∴Rt△DCE≌Rt△FHE.∴CD=HF.
【例2】如图,在☉O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB.
(2)若∠DBE=37°,求∠ADC的度数.
【标准解答】(1)∵AB,CD是直径,
∴∠ADB=∠CBD=90°,
在△ABD和△CDB中,
∴Rt△ABD≌Rt△CDB(HL).
(2)∵BE是切线,∴AB⊥BE,
∴∠ABE=90°,
∵∠DBE=37°,∴∠ABD=53°,
∵OA=OD,
∴∠BAD=∠ODA=90°-53°=37°,
∴∠ADC的度数为37°.
1.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是☉O的切线.
(2)若BF=8,DF=,求☉O的半径r.
2.如图,AB为☉O的直径,PD切☉O于点C,交AB的延长线于点D,且∠D=2∠CAD.
(1)求∠D的度数.
(2)若CD=2,求BD的长.
3.如图,在△ABC中,AB=AC,以AB为直径的☉O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)试说明DF是☉O的切线.
(2)若AC=3AE,求tanC.
4.三角形的外接圆与内切圆
(1)三角形的外心是三角形三边垂直平分线的交点,它到三角形三个顶点的距离都相等.直角三角形外接圆的半径等于斜边的一半.
(2)三角形的内心是三角形三条角平分线的交点,它到三角形三条边的距离相等.直角三角形内切圆的半径r=(其中a,b为直角边,c为斜边).
【例1】如图,△ABC的外心坐标是 .
【标准解答】∵△ABC的外心即是三角形三边垂直平分线的交点,∴作图如图,
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(-2,-1).
答案:(-2,-1)
【例2】△ABC的内切圆☉O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
【标准解答】根据切线长定理,设AE=AF=xcm,BF=BD=ycm,CE=CD=zcm.根据题意,得
解得
即AF=4cm,BD=5cm,CE=9cm.
1.如图所示,△ABC内接于☉O,若∠OAB=28°,则∠C的大小是 ( )
A.56° B.62° C.28° D.32°
1题图
2题图
2.如图,已知☉O是边长为2的等边△ABC的内切圆,则☉O的面积为 .
5.正多边形的有关计算
正多边形的半径、边心距、边长的一半构成一个直角三角形.正多边形的有关计算问题都可归结到这个直角三角形中.
【例】一个正三角形和一个正六边形的面积相等,求它们边长的比.
【标准解答】如图,设O,O′分别是正三角形ABC、正六边形EFGHIJ的中心,分别作OD⊥BC于D,作O′K⊥GH于K,连接OB,O′G,则在Rt△ODB中,∠BOD==
60°,BD=a3,
∴∠OBD=30°.
∴OB=2OD=2r3,由勾股定理得
OB2=OD2+BD2,即(2r3)2=+(a3)2
解得r3=a3,
∴S3=6S△BOD=6××BD×OD=6××a3×a3=.
同理可得S6=12S△O′GK=12××GK×O′K=12××a6×a6=,
∵S3=S6,∴=,
∴=.∴=,即a3∶a6=∶1.
1.如图,正六边形ABCDEF内接于☉O,若直线PA与☉O相切于点A,则
∠PAB=( )
A.30° B.35° C.45° D.60°
1题图
2题图
2.如图,☉O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是 ( )
A.R2-r2=a2 B.a=2Rsin 36°
C.a=2rtan 36° D.r=Rcos 36°
3.图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.
(1)如图②,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于 .
6.求阴影部分面积的方法
(1)割补法
将不规则图形进行割补转化为规则图形来计算.
【例1】如图,阴影部分的面积为 .
【标准解答】如图,四边形ABEF和四边形ECDF为正方形,且边长为a,那么扇形BEF的面积等于扇形CED的面积,所以图形1的面积等于图形3的面积,则阴影部分的面积=图形1的面积+图形2的面积=正方形ABEF的面积=a2.
答案:a2
(2)和差法
将阴影部分的面积看成几个规则图形面积的和或差来进行计算.
【例2】如图,在△ABC中,AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分面积是 ( )
A.50π-48 B.25π-48
C.50π-24 D.π-24
【标准解答】选B.设以AB,AC为直径作半圆交BC于D点,连AD,如图,
∴AD⊥BC,
∴BD=DC=BC=8,AB=AC=10,
∴AD===6,
∴阴影部分面积=半圆AC的面积+半圆AB的面积-△ABC的面积=π×52-×16×6=25π-48.
(3)平移法
通过图形的平移,将不规则图形的面积转化为规则图形的面积来计算.
【例3】如图,两个半圆中,小圆的圆心O′在大☉O的直径CD上,长为4的弦AB与直径CD平行且与小半圆相切,那么图中阴影部分的面积等于 .
【标准解答】把小半圆向右平移,使两个圆心重合时,小半圆的面积不变,因而阴影部分的面积未变;连接OB,作OP⊥AB于P,因而阴影部分的面积是大半圆的面积减去小半圆的面积,阴影部分的面积=π·OB2-π·OP2=π·(OB2-OP2)=π·BP2=
2π.
答案:2π
(4)等积法
将不规则的阴影部分的面积用和它面积相等的规则图形替代,然后计算规则的图形的面积.
【例4】如图所示,正方形ABCD内接于☉O,直径MN∥AD,则阴影部分面积占圆面积的 ( )
A. B. C. D.
【标准解答】选B.连接OD,OC.∵MN∥AD∥BC,ON=ON,∴四边形BOAN的面积=四边形CODN的面积.
再根据图形的轴对称性,得阴影部分的面积=扇形DOC的面积=圆面积.
(5)方程(组)法
当阴影部分面积不好直接求解时可用列方程(组)的方法求解.
【例5】如图所示,正方形ABCD的边长为a,以A为圆心作,以AB为直径作,M是AD上一点,以DM为直径,作与相外切,则图中阴影部分面积为 .
【标准解答】设以DM为直径的半圆的圆心为O1,半径为r,以AB为直径的半圆的圆心为O2,连接O1O2,则有(a-r)2+=,解得:r=a,所以S阴影=
S扇形DAB--=πa2-π-π=πa2.
答案:πa2
1.如图,扇形AOB中,半径OA=2,∠AOB=120°,C是弧AB的中点,连接AC,BC,则图中阴影部分的面积是 ( )
A.-2 B.-2
C.- D.-
1题图
2题图
3题图
2.如图,AB是☉O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影= ( )
A.π B. 2π C. D.π
3.如图所示,AB为半圆O的直径,C,D,E,F是上的五等分点,P为直径AB上的任意一点,若AB=4,则图中阴影部分的面积为 .
4.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC.把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 .(结果保留π)
5.如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作☉O交BA延长线于点D,连接CD.
(1)求证:CD是☉O的切线.
(2)若AB=4,求图中阴影部分的面积.
6.如图,PA,PB分别与☉O相切于A,B两点,∠ACB=60°.
(1)求∠P的度数.
(2)若☉O的半径长为4cm,求图中阴影部分的面积.
7.如图,四边形ABCD是☉O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E.
(1)求∠OCA的度数.
(2)若∠COB=3∠AOB,OC=2,求图中阴影部分面积.(结果保留π和根号)
8.如图,AB是☉O的直径,=,连接ED,BD,延长AE交BD的延长线于点M,过点D作☉O的切线交AB的延长线于点C.
(1)若OA=CD=2,求阴影部分的面积.
(2)求证:DE=DM.
跟踪训练答案解析
第三章 圆
1.解决与弦有关的问题
【跟踪训练】
1.【解析】选C.连接OA,
∵CD是☉O的直径,AB是☉O的弦,AB⊥CD,∴AB=2AM,∵CD=5cm,
∴OD=OA=CD=×5=(cm),
∵OM∶OD=3∶5,
∴OM=OD=×=(cm),
∴在Rt△AOM中,AM==2,∴AB=2AM=2×2=4(cm).
2.【解析】选C.∵∠A=22.5°,∴∠COB=45°,
在Rt△COE中,
∵OC=4,∴CE=2,∴CD=2CE=4.
3.【解析】选C.过A作AD⊥BC,由题意可知AD必过点O,连接OB;
∵△BAC是等腰直角三角形,AD⊥BC,
∴BD=CD=AD=3;∴OD=AD-OA=2;
在Rt△OBD中,根据勾股定理,得:
OB==.
2.与圆心角、圆周角有关的问题
【跟踪训练】
1.【解析】选A.由垂径定理,得=,
∴∠CDB=∠AOC=25°.
2.【解析】选C.连接AD,
∵AB是☉O的直径,
∴∠ADB=90°,
∵由圆周角定理可知∠ADE=∠ACE,
∴∠ACE+∠BDE=∠ADB=90°.
3.【解析】连接BD,则∠CBD=∠CAD=35°,因四边形ABDE是圆内接四边形,∴∠ABD+∠E=180°,∴∠ABC+∠E=215°.
答案:215
4.【证明】方法一:连接BC,
∵AB是直径,
∴∠ACB=90°,
即∠ACF+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∴∠B=∠ACF,
∵C是的中点,∴=,
∴∠B=∠CAF,∴∠ACF=∠CAF,
∴AF=CF.
方法二:延长CD交圆于点H,
∵AB是直径,CD⊥AB,∴=,
∵C是的中点,∴=,
∴=,∴∠ACF=∠CAE,
∴AF=CF.
3.切线的判定与性质
【跟踪训练】
1.【解析】(1)连接OA,OD,则OA=OD,
∴∠OAD=∠ODA,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,∴∠ODA+∠OFD=90°,∴∠OAD+∠OFD=90°,
∵∠OFD=∠AFC,
∴∠OAD+∠AFC=90°,
∵AC=FC,∴∠FAC=∠AFC,
∴∠OAD+∠FAC=90°,
∴AC是☉O的切线.
(2)BF=8,DF=,∴OF=8-r,
∴在直角三角形OFD中,
r2+(8-r)2=()2,解得,r=2.
2.【解析】(1)∵OA=OC,∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵∠D=2∠CAD,∴∠D=∠COD,
∵PD切☉O于C,∴∠OCD=90°,
∴∠D=∠COD=45°.
(2)∵∠D=∠COD,CD=2,
∴OC=OB=CD=2,
在Rt△OCD中,由勾股定理得:22+22=(2+BD)2,解得:BD=2-2.
3.【解析】(1)连接OD,则OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠C,
∴∠ODB=∠C,∴OD∥AC,
∵DF⊥AC,∴DF⊥OD,
∵DF经过半径OD的外端,
∴DF是☉O的切线.
(2)连接BE,∵AB为☉O的直径,
∴∠E=90°,
设AE=k,则AB=AC=3k,
∴BE===2k,
∴tanC===.
4.三角形的外接圆与内切圆
【跟踪训练】
1.【解析】选B.连接OB,∵OA=OB,
∴△AOB是等腰三角形,∴∠OAB=∠OBA,
∵∠OAB=28°,∴∠OAB=∠OBA=28°,
∴∠AOB=124°,∴∠C=62°.
2.【解析】设BC切☉O于点D,连接OC,OD;
∵CA,CB都与☉O相切,
∴∠OCD=∠OCA=30°.
在Rt△OCD中,
CD=BC=1,∠OCD=30°,
∴OD=OC,
∵在Rt△ODC中,OD2+CD2=OC2,
∴OD==,∴S☉O=π(OD)2=.
答案:
5.正多边形的有关计算
【跟踪训练】
1.【解析】选A.连接OA,根据直线PA为切线可得∠OAP=90°,根据正六边形的性质可得∠OAB=60°,则∠PAB=∠OAP-∠OAB=90°-60°=
30°.
2.【解析】选A.∵☉O是正五边形ABCDE的外接圆,∴∠BOC=×
360°=72°,
∴∠1=∠BOC=×72°=36°,
R2-r2==a2,
a=Rsin 36°,a=2Rsin 36°;
a=rtan 36°,a=2rtan 36°,
cos 36°=,r=Rcos 36°,
所以,关系式错误的是R2-r2=a2.
3.【解析】(1)如图所示,八边形ABCDEFGH即为所求,
(2)∵八边形ABCDEFGH是正八边形,
∴∠AOD=3×45°=135°,
∵OA=5,
∴的长==π,
设这个圆锥底面圆的半径为R,
∴2πR=π,
∴R=,即这个圆锥底面圆的半径为.
答案:
6.求阴影部分面积的方法
【跟踪训练】
1.【解析】选A.连接OC,得∠AOC=∠BOC=60°,△OAC,△BOC都是等边三角形.
∴S△AOC=×22=,
∴S阴影=2=-2.
2.【解析】选D.设CD⊥AB交AB于点E,
∵AB是直径,∴CE=DE=CD=,
又∵∠CDB=30°,∴∠COE=60°,
∴OE=1,OC=2,∴BE=1,
∴S△BED=S△OEC,
∴S阴影=S扇形BOC==.
3.【解析】连接OD,OE.∵C,D,E,F是上的五等分点,
∴∠DOE=×180°=36°,
∴S扇形DOE==π.
答案:π
4.【解析】∵∠ACB=90°,CB=AC,AB=2,
∴AC=BC=,∵△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,
∴AC′=AC=,AB′=AB=2,∠BAB′=45°,∠B′AC′=45°,
∴S阴影部分=+--=
-=-=.
答案:
5.【解析】(1)连接OD,
∵∠BCA=90°,
∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,∴△OAD是等边三角形,
∴AD=OA=AC,
∠ODA=∠O=60°,
∴∠ADC=∠ACD=∠OAD=30°,
∴∠ODC=60°+30°=90°,即OD⊥DC,
∵OD为半径,∴CD是☉O的切线.
(2)∵AB=4,∠ACB=90°,∠B=30°,
∴OD=OA=AC=AB=2,
由勾股定理得:
CD===2,
∴S阴影=-S扇形AOD=×2×2-=2-π.
6.【解析】(1)连接OA,OB,
∵PA,PB是☉O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,
又∵∠AOB=2∠C=120°,
∴∠APB=360°-(90°+90°+120°)=60°.
∴∠APB=60°.
(2)连接OP交于点D,
∵PA,PB是☉O的切线,
∴∠APO=∠APB=30°,
在Rt△APO中,tan 30°=,
∴AP===4(cm),
∴S阴影=2(S△AOP-S扇形AOD)
=2×
=.
7.【解析】(1)∵四边形ABCD是☉O的内接四边形,∴∠ABC+∠D=180°,
∵∠ABC=2∠D,∴∠D+2∠D=180°,
∴∠D=60°,∴∠AOC=2∠D=120°,
∵OA=OC,∴∠OAC=∠OCA=30°.
(2)∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2,
∴OE=OC·tan∠OCE=2·tan 30°
=2×=2,
∴S△OEC=OE·OC=×2×2=2,
∴S扇形OBC==3π,
∴S阴影=S扇形OBC-S△OEC=3π-2.
8.【解析】(1)如图,连接OD,
∵CD是☉O切线,∴OD⊥CD,
∵OA=CD=2,OA=OD,
∴OD=CD=2,
∴△OCD为等腰直角三角形,
∴∠DOC=∠C=45°,
∴S阴影=S△OCD-S扇形OBD=×2×2-=4-π.
(2)如图,连接AD,
∵AB是☉O的直径,
∴∠ADB=∠ADM=90°,
又∵=,
∴ED=BD,∠MAD=∠BAD,
在△AMD和△ABD中,
∴△AMD≌△ABD,
∴DM=BD,∴DE=DM.
1.解决与弦有关的问题
垂径定理和勾股定理有机结合计算弦长、半径、圆心到弦的距离等问题的方法——构造直角三角形;在圆中解决与弦有关问题经常作的辅助线——圆心到弦的距离.
【例】如图,平面直角坐标系中,☉P与x轴分别交于A,B两点,点P的坐标为(3,-1),AB=2.
(1)求☉P的半径.
(2)将☉P向下平移,求☉P与x轴相切时平移的距离.
【标准解答】(1)作PC⊥AB于C,连接PA.∴AC=CB=AB.
∵AB=2,∴AC=.
∵点P的坐标为(3,-1),∴PC=1.
在Rt△PAC中,∠PCA=90°,
∴PA===2.
∴☉P的半径为2.
(2)将☉P向下平移,☉P与x轴相切时平移的距离为2-1=1.
1.如图,☉O的直径CD=5cm,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OD=3∶5.则AB的长是 ( )
A.2 cm B.3 cm
C.4 cm D.2cm
1题图
2题图
2.如图☉O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为
( )
A.2 B.4 C.4 D.8
3.☉O过点B,C,圆心O在等腰直角△ABC内部,∠BAC=90°,OA=1,BC=6,则☉O的半径为 ( )
A. B.2
C. D.3
2.与圆心角、圆周角有关的问题
(1)利用圆周角定理将圆心角与圆周角进行转化.
(2)利用同弧所对的圆周角相等进行角与角的转化.
(3)利用直径所对的圆周角是直角构造直角三角形,为勾股定理、解直角三角形等知识的应用创造条件.
(4)利用圆内接四边形的性质求圆心角或圆周角.
【例1】如图,☉O中,弦AB,CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于
( )
A.30° B.35° C.40° D.50°
【标准解答】选C.∵∠APD是△APC的外角,∴∠APD=∠C+∠A;
∵∠A=30°,∠APD=70°,
∴∠C=∠APD-∠A=40°.
∴∠B=∠C=40°.
【例2】如图,将三角板的直角顶点放在☉O的圆心上,两条直角边分别交☉O于A,B两点,点P在优弧AB上,且与点A,B不重合,连接PA,PB,则∠APB的大小为 度.
【标准解答】∵∠AOB与∠APB为所对的圆心角和圆周角,
∴∠APB=∠AOB=×90°=45°.
答案:45
【例3】如图,☉O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是 .
【标准解答】连接AD,
∵CD是直径,
∴∠CAD=90°,
∵∠B=40°,
∴∠D=40°,
∴∠ACD=50°.
答案:50°
【例4】如图,四边形ABCD内接于☉O,AD∥BC,∠DAB=49°,则∠AOC的度数为 .
【标准解答】如图,在上取点M,连接AM,CM,
∵AD∥BC,∠DAB=49°,
∴∠ABC=131°,
∴∠M=49°,
∠AOC=98°.
答案:98°
1.如图,☉O的直径CD⊥AB,∠AOC=50°,则∠CDB的大小为 ( )
A.25° B.30° C.40° D.50°
1题图
2题图
3题图
2.如图,AB是☉O的直径,C,D,E都是☉O上的点,则∠ACE+∠BDE= ( )
A.60° B.75° C.90° D.120°
3.如图,在☉O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E= °.
4.如图,AB是☉O的直径,C是弧AE的中点,CD⊥AB于D,交AE于F,连接AC,试证明AF=CF.
3.切线的判定与性质
(1)切线的三种判定方法
①从公共点的个数来判断:直线与圆有且只有一个公共点;
②从圆心到直线的距离来判断:圆心到直线的距离等于圆的半径;
③应用判定定理:经过半径外端且与半径垂直.
(2)利用切线的判定定理的两个思路
①连半径,证垂直:
若已知直线与圆有公共点,则连接圆心和公共点,证明垂直.
②作垂线,证等径:
若直线与圆的公共点没有确定,则过圆心作直线的垂线,证明圆心到直线的距离等于半径.
(3)切线性质应用的两个思路
①有切点:连接切点和半径,必垂直,建直角三角形;
②无切点:过圆心作半径,必垂直,得切点,建直角三角形.
【例1】如图,在△ABC中,∠C=90°①,∠ABC的平分线交AC于点E②,过点E作BE的垂线于点F③,☉O是△BEF的外接圆.
(1)求证:AC是☉O的切线④.
(2)过点E作EH⊥AB于点H⑤,
求证:CD=HF.
【信息解读·破译解题秘钥】
条件②直译为:∠CBE=∠FBE⑥.
条件③翻译为:BF为圆O的直径.
破译:连接OE,则可得∠OBE=∠OEB,整合条件②③,可得OE∥BC⑦.
破译:整合条件①⑥⑦得到OE⊥AC,进而得到AC是☉O的切线.
条件②翻译为:=,进而得到DE=EF⑧.
破译:整合条件①②⑤,得到CE=EH⑨.
破译:整合条件①⑤⑧⑨,得到△ECD≌△EHF,进而得到CD=HF.
【标准解答】(1)连接OE.
∵BE⊥EF,
∴∠BEF=90°,
∴BF为☉O的直径.
∵BE平分∠ABC,
∴∠OBE=∠CBE.
∵OB=OE,∴∠OBE=∠OEB.
∴∠CBE=∠OEB.∴OE∥BC.
∴∠OEA=∠C=90°.∴OE⊥AC.
∴AC是☉O的切线.
(2)连接DE.
∵∠OBE=∠CBE,∴=.
∴DE=EF.
∵BE平分∠ABC,EC⊥BC,EH⊥AB,
∴EC=EH.
又∵∠C=∠EHF=90°,DE=EF,
∴Rt△DCE≌Rt△FHE.∴CD=HF.
【例2】如图,在☉O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB.
(2)若∠DBE=37°,求∠ADC的度数.
【标准解答】(1)∵AB,CD是直径,
∴∠ADB=∠CBD=90°,
在△ABD和△CDB中,
∴Rt△ABD≌Rt△CDB(HL).
(2)∵BE是切线,∴AB⊥BE,
∴∠ABE=90°,
∵∠DBE=37°,∴∠ABD=53°,
∵OA=OD,
∴∠BAD=∠ODA=90°-53°=37°,
∴∠ADC的度数为37°.
1.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是☉O的切线.
(2)若BF=8,DF=,求☉O的半径r.
2.如图,AB为☉O的直径,PD切☉O于点C,交AB的延长线于点D,且∠D=2∠CAD.
(1)求∠D的度数.
(2)若CD=2,求BD的长.
3.如图,在△ABC中,AB=AC,以AB为直径的☉O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)试说明DF是☉O的切线.
(2)若AC=3AE,求tanC.
4.三角形的外接圆与内切圆
(1)三角形的外心是三角形三边垂直平分线的交点,它到三角形三个顶点的距离都相等.直角三角形外接圆的半径等于斜边的一半.
(2)三角形的内心是三角形三条角平分线的交点,它到三角形三条边的距离相等.直角三角形内切圆的半径r=(其中a,b为直角边,c为斜边).
【例1】如图,△ABC的外心坐标是 .
【标准解答】∵△ABC的外心即是三角形三边垂直平分线的交点,∴作图如图,
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(-2,-1).
答案:(-2,-1)
【例2】△ABC的内切圆☉O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
【标准解答】根据切线长定理,设AE=AF=xcm,BF=BD=ycm,CE=CD=zcm.根据题意,得
解得
即AF=4cm,BD=5cm,CE=9cm.
1.如图所示,△ABC内接于☉O,若∠OAB=28°,则∠C的大小是 ( )
A.56° B.62° C.28° D.32°
1题图
2题图
2.如图,已知☉O是边长为2的等边△ABC的内切圆,则☉O的面积为 .
5.正多边形的有关计算
正多边形的半径、边心距、边长的一半构成一个直角三角形.正多边形的有关计算问题都可归结到这个直角三角形中.
【例】一个正三角形和一个正六边形的面积相等,求它们边长的比.
【标准解答】如图,设O,O′分别是正三角形ABC、正六边形EFGHIJ的中心,分别作OD⊥BC于D,作O′K⊥GH于K,连接OB,O′G,则在Rt△ODB中,∠BOD==
60°,BD=a3,
∴∠OBD=30°.
∴OB=2OD=2r3,由勾股定理得
OB2=OD2+BD2,即(2r3)2=+(a3)2
解得r3=a3,
∴S3=6S△BOD=6××BD×OD=6××a3×a3=.
同理可得S6=12S△O′GK=12××GK×O′K=12××a6×a6=,
∵S3=S6,∴=,
∴=.∴=,即a3∶a6=∶1.
1.如图,正六边形ABCDEF内接于☉O,若直线PA与☉O相切于点A,则
∠PAB=( )
A.30° B.35° C.45° D.60°
1题图
2题图
2.如图,☉O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是 ( )
A.R2-r2=a2 B.a=2Rsin 36°
C.a=2rtan 36° D.r=Rcos 36°
3.图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.
(1)如图②,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于 .
6.求阴影部分面积的方法
(1)割补法
将不规则图形进行割补转化为规则图形来计算.
【例1】如图,阴影部分的面积为 .
【标准解答】如图,四边形ABEF和四边形ECDF为正方形,且边长为a,那么扇形BEF的面积等于扇形CED的面积,所以图形1的面积等于图形3的面积,则阴影部分的面积=图形1的面积+图形2的面积=正方形ABEF的面积=a2.
答案:a2
(2)和差法
将阴影部分的面积看成几个规则图形面积的和或差来进行计算.
【例2】如图,在△ABC中,AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分面积是 ( )
A.50π-48 B.25π-48
C.50π-24 D.π-24
【标准解答】选B.设以AB,AC为直径作半圆交BC于D点,连AD,如图,
∴AD⊥BC,
∴BD=DC=BC=8,AB=AC=10,
∴AD===6,
∴阴影部分面积=半圆AC的面积+半圆AB的面积-△ABC的面积=π×52-×16×6=25π-48.
(3)平移法
通过图形的平移,将不规则图形的面积转化为规则图形的面积来计算.
【例3】如图,两个半圆中,小圆的圆心O′在大☉O的直径CD上,长为4的弦AB与直径CD平行且与小半圆相切,那么图中阴影部分的面积等于 .
【标准解答】把小半圆向右平移,使两个圆心重合时,小半圆的面积不变,因而阴影部分的面积未变;连接OB,作OP⊥AB于P,因而阴影部分的面积是大半圆的面积减去小半圆的面积,阴影部分的面积=π·OB2-π·OP2=π·(OB2-OP2)=π·BP2=
2π.
答案:2π
(4)等积法
将不规则的阴影部分的面积用和它面积相等的规则图形替代,然后计算规则的图形的面积.
【例4】如图所示,正方形ABCD内接于☉O,直径MN∥AD,则阴影部分面积占圆面积的 ( )
A. B. C. D.
【标准解答】选B.连接OD,OC.∵MN∥AD∥BC,ON=ON,∴四边形BOAN的面积=四边形CODN的面积.
再根据图形的轴对称性,得阴影部分的面积=扇形DOC的面积=圆面积.
(5)方程(组)法
当阴影部分面积不好直接求解时可用列方程(组)的方法求解.
【例5】如图所示,正方形ABCD的边长为a,以A为圆心作,以AB为直径作,M是AD上一点,以DM为直径,作与相外切,则图中阴影部分面积为 .
【标准解答】设以DM为直径的半圆的圆心为O1,半径为r,以AB为直径的半圆的圆心为O2,连接O1O2,则有(a-r)2+=,解得:r=a,所以S阴影=
S扇形DAB--=πa2-π-π=πa2.
答案:πa2
1.如图,扇形AOB中,半径OA=2,∠AOB=120°,C是弧AB的中点,连接AC,BC,则图中阴影部分的面积是 ( )
A.-2 B.-2
C.- D.-
1题图
2题图
3题图
2.如图,AB是☉O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影= ( )
A.π B. 2π C. D.π
3.如图所示,AB为半圆O的直径,C,D,E,F是上的五等分点,P为直径AB上的任意一点,若AB=4,则图中阴影部分的面积为 .
4.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC.把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 .(结果保留π)
5.如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作☉O交BA延长线于点D,连接CD.
(1)求证:CD是☉O的切线.
(2)若AB=4,求图中阴影部分的面积.
6.如图,PA,PB分别与☉O相切于A,B两点,∠ACB=60°.
(1)求∠P的度数.
(2)若☉O的半径长为4cm,求图中阴影部分的面积.
7.如图,四边形ABCD是☉O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E.
(1)求∠OCA的度数.
(2)若∠COB=3∠AOB,OC=2,求图中阴影部分面积.(结果保留π和根号)
8.如图,AB是☉O的直径,=,连接ED,BD,延长AE交BD的延长线于点M,过点D作☉O的切线交AB的延长线于点C.
(1)若OA=CD=2,求阴影部分的面积.
(2)求证:DE=DM.
跟踪训练答案解析
第三章 圆
1.解决与弦有关的问题
【跟踪训练】
1.【解析】选C.连接OA,
∵CD是☉O的直径,AB是☉O的弦,AB⊥CD,∴AB=2AM,∵CD=5cm,
∴OD=OA=CD=×5=(cm),
∵OM∶OD=3∶5,
∴OM=OD=×=(cm),
∴在Rt△AOM中,AM==2,∴AB=2AM=2×2=4(cm).
2.【解析】选C.∵∠A=22.5°,∴∠COB=45°,
在Rt△COE中,
∵OC=4,∴CE=2,∴CD=2CE=4.
3.【解析】选C.过A作AD⊥BC,由题意可知AD必过点O,连接OB;
∵△BAC是等腰直角三角形,AD⊥BC,
∴BD=CD=AD=3;∴OD=AD-OA=2;
在Rt△OBD中,根据勾股定理,得:
OB==.
2.与圆心角、圆周角有关的问题
【跟踪训练】
1.【解析】选A.由垂径定理,得=,
∴∠CDB=∠AOC=25°.
2.【解析】选C.连接AD,
∵AB是☉O的直径,
∴∠ADB=90°,
∵由圆周角定理可知∠ADE=∠ACE,
∴∠ACE+∠BDE=∠ADB=90°.
3.【解析】连接BD,则∠CBD=∠CAD=35°,因四边形ABDE是圆内接四边形,∴∠ABD+∠E=180°,∴∠ABC+∠E=215°.
答案:215
4.【证明】方法一:连接BC,
∵AB是直径,
∴∠ACB=90°,
即∠ACF+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
∴∠B=∠ACF,
∵C是的中点,∴=,
∴∠B=∠CAF,∴∠ACF=∠CAF,
∴AF=CF.
方法二:延长CD交圆于点H,
∵AB是直径,CD⊥AB,∴=,
∵C是的中点,∴=,
∴=,∴∠ACF=∠CAE,
∴AF=CF.
3.切线的判定与性质
【跟踪训练】
1.【解析】(1)连接OA,OD,则OA=OD,
∴∠OAD=∠ODA,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,∴∠ODA+∠OFD=90°,∴∠OAD+∠OFD=90°,
∵∠OFD=∠AFC,
∴∠OAD+∠AFC=90°,
∵AC=FC,∴∠FAC=∠AFC,
∴∠OAD+∠FAC=90°,
∴AC是☉O的切线.
(2)BF=8,DF=,∴OF=8-r,
∴在直角三角形OFD中,
r2+(8-r)2=()2,解得,r=2.
2.【解析】(1)∵OA=OC,∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵∠D=2∠CAD,∴∠D=∠COD,
∵PD切☉O于C,∴∠OCD=90°,
∴∠D=∠COD=45°.
(2)∵∠D=∠COD,CD=2,
∴OC=OB=CD=2,
在Rt△OCD中,由勾股定理得:22+22=(2+BD)2,解得:BD=2-2.
3.【解析】(1)连接OD,则OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠C,
∴∠ODB=∠C,∴OD∥AC,
∵DF⊥AC,∴DF⊥OD,
∵DF经过半径OD的外端,
∴DF是☉O的切线.
(2)连接BE,∵AB为☉O的直径,
∴∠E=90°,
设AE=k,则AB=AC=3k,
∴BE===2k,
∴tanC===.
4.三角形的外接圆与内切圆
【跟踪训练】
1.【解析】选B.连接OB,∵OA=OB,
∴△AOB是等腰三角形,∴∠OAB=∠OBA,
∵∠OAB=28°,∴∠OAB=∠OBA=28°,
∴∠AOB=124°,∴∠C=62°.
2.【解析】设BC切☉O于点D,连接OC,OD;
∵CA,CB都与☉O相切,
∴∠OCD=∠OCA=30°.
在Rt△OCD中,
CD=BC=1,∠OCD=30°,
∴OD=OC,
∵在Rt△ODC中,OD2+CD2=OC2,
∴OD==,∴S☉O=π(OD)2=.
答案:
5.正多边形的有关计算
【跟踪训练】
1.【解析】选A.连接OA,根据直线PA为切线可得∠OAP=90°,根据正六边形的性质可得∠OAB=60°,则∠PAB=∠OAP-∠OAB=90°-60°=
30°.
2.【解析】选A.∵☉O是正五边形ABCDE的外接圆,∴∠BOC=×
360°=72°,
∴∠1=∠BOC=×72°=36°,
R2-r2==a2,
a=Rsin 36°,a=2Rsin 36°;
a=rtan 36°,a=2rtan 36°,
cos 36°=,r=Rcos 36°,
所以,关系式错误的是R2-r2=a2.
3.【解析】(1)如图所示,八边形ABCDEFGH即为所求,
(2)∵八边形ABCDEFGH是正八边形,
∴∠AOD=3×45°=135°,
∵OA=5,
∴的长==π,
设这个圆锥底面圆的半径为R,
∴2πR=π,
∴R=,即这个圆锥底面圆的半径为.
答案:
6.求阴影部分面积的方法
【跟踪训练】
1.【解析】选A.连接OC,得∠AOC=∠BOC=60°,△OAC,△BOC都是等边三角形.
∴S△AOC=×22=,
∴S阴影=2=-2.
2.【解析】选D.设CD⊥AB交AB于点E,
∵AB是直径,∴CE=DE=CD=,
又∵∠CDB=30°,∴∠COE=60°,
∴OE=1,OC=2,∴BE=1,
∴S△BED=S△OEC,
∴S阴影=S扇形BOC==.
3.【解析】连接OD,OE.∵C,D,E,F是上的五等分点,
∴∠DOE=×180°=36°,
∴S扇形DOE==π.
答案:π
4.【解析】∵∠ACB=90°,CB=AC,AB=2,
∴AC=BC=,∵△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,
∴AC′=AC=,AB′=AB=2,∠BAB′=45°,∠B′AC′=45°,
∴S阴影部分=+--=
-=-=.
答案:
5.【解析】(1)连接OD,
∵∠BCA=90°,
∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,∴△OAD是等边三角形,
∴AD=OA=AC,
∠ODA=∠O=60°,
∴∠ADC=∠ACD=∠OAD=30°,
∴∠ODC=60°+30°=90°,即OD⊥DC,
∵OD为半径,∴CD是☉O的切线.
(2)∵AB=4,∠ACB=90°,∠B=30°,
∴OD=OA=AC=AB=2,
由勾股定理得:
CD===2,
∴S阴影=-S扇形AOD=×2×2-=2-π.
6.【解析】(1)连接OA,OB,
∵PA,PB是☉O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,
又∵∠AOB=2∠C=120°,
∴∠APB=360°-(90°+90°+120°)=60°.
∴∠APB=60°.
(2)连接OP交于点D,
∵PA,PB是☉O的切线,
∴∠APO=∠APB=30°,
在Rt△APO中,tan 30°=,
∴AP===4(cm),
∴S阴影=2(S△AOP-S扇形AOD)
=2×
=.
7.【解析】(1)∵四边形ABCD是☉O的内接四边形,∴∠ABC+∠D=180°,
∵∠ABC=2∠D,∴∠D+2∠D=180°,
∴∠D=60°,∴∠AOC=2∠D=120°,
∵OA=OC,∴∠OAC=∠OCA=30°.
(2)∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2,
∴OE=OC·tan∠OCE=2·tan 30°
=2×=2,
∴S△OEC=OE·OC=×2×2=2,
∴S扇形OBC==3π,
∴S阴影=S扇形OBC-S△OEC=3π-2.
8.【解析】(1)如图,连接OD,
∵CD是☉O切线,∴OD⊥CD,
∵OA=CD=2,OA=OD,
∴OD=CD=2,
∴△OCD为等腰直角三角形,
∴∠DOC=∠C=45°,
∴S阴影=S△OCD-S扇形OBD=×2×2-=4-π.
(2)如图,连接AD,
∵AB是☉O的直径,
∴∠ADB=∠ADM=90°,
又∵=,
∴ED=BD,∠MAD=∠BAD,
在△AMD和△ABD中,
∴△AMD≌△ABD,
∴DM=BD,∴DE=DM.
