2019版九年级数学下册第二章 二次函数复习学案(含解析)
文档属性
| 名称 | 2019版九年级数学下册第二章 二次函数复习学案(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-23 08:21:59 | ||
图片预览




文档简介
第二章 二次函数
1.二次函数y=ax2+bx+c的配方步骤
(1)提:提取二次项系数,把二次项系数化为1.
(2)配:把括号内配成完全平方公式.
(3)化:把函数关系式化成顶点式.
【例】配方:y=4x2-8x.
【标准解答】y=4x2-8x =4(x2-2x)
=4(x2-2x+1-1)=4(x-1)2-4.
1.二次函数y=-x2+2x+4的最大值为( )
A.3 B.4 C.5 D.6
2.将二次函数y=x2-4x+5化为y=(x-h)2+k的形式,则y= .
3.二次函数y=x2+2x的顶点坐标为 ,对称轴是直线 .
2.确定二次函数解析式的方法
(1)一般式:若已知条件是图象上的三点,则用y=ax2+bx+c,将已知三个点的坐标代入,求出a,b,c的值.
【例1】已知二次函数的图象经过(0,1),(2,1)和(3,4),求该二次函数的解析式.
【标准解答】设函数解析式为y=ax2+bx+c,
则解得
∴y=x2-2x+1.
(2)顶点式:若已知二次函数图象的顶点坐标或对称轴方程与最大值(或最小值),设所求二次函数为y=a(x-h)2+k,将已知条件代入,求出待定系数.
【例2】根据函数图象写出二次函数的解析式.
【标准解答】由图象知抛物线对称轴x=-1,顶点坐标为(-1,2),过原点(0,0),点(-2,0).
设解析式为y=a(x+1)2+2,
∵过原点(0,0),∴a+2=0,a=-2.
故解析式为y=-2(x+1)2+2,即y=-2x2-4x.
(3)交点式:若已知二次函数图象与x轴的两个交点的坐标为(x1,0),(x2,0),设所求二次函数为y=a(x-x1)(x-x2),将第三点(m,n)的坐标(其中m,n为已知数)或其他已知条件代入,求出待定系数a.
【例3】已知函数y=ax2+bx+c的图象如图,那么函数解析式为 ( )
A.y=-x2+2x+3
B.y=x2-2x-3
C.y=-x2-2x+3
D.y=-x2-2x-3
【标准解答】选A.运用二次函数交点式:y=a(x-x1)(x-x2),则y=a(x+1)(x-3),把(0,3)代入,则a=-1,整理,得y=-x2+2x+3.
(4)根据平移确定解析式:先把抛物线化成顶点式y=a(x-h)2+k,然后根据h值左加右减,k值上加下减来进行.
【例4】抛物线y=(x+2)2-3可以由抛物线y=x2平移得到,则下列平移过程正确的是 ( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
【标准解答】选B.y=(x+2)2-3的顶点为(-2,-3),抛物线y=x2的顶点为(0,0),所以平移的过程是先向左平移2个单位,再向下平移3个单位.
1.将抛物线y=-2x2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为 ( )
A.y=-2(x+1)2
B.y=-2(x+1)2+2
C.y=-2(x-1)2+2
D.y=-2(x-1)2+1
2.将抛物线y=x2的图象向上平移1个单位,则平移后的抛物线的解析式为 .
3.设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 .
4.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:
温度t/℃
-4
-2
0
1
4
植物高度增
长量l/mm
41
49
49
46
25
经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为 ℃.
3.二次函数y=ax2+bx+c中的系数值对抛物线的影响
二次函数y=ax2+bx+c的图象特征与a,b,c的符号有密切联系,它们的关系如下:
(1)二次项系数a决定抛物线的开口方向、函数最值情况.
①a>0?开口向上,函数有最小值;
②a<0?开口向下,函数有最大值.
(2)常数项c决定抛物线与y轴的交点,交点坐标为(0,c).
①c>0?交点在y轴正半轴上;
②c=0?抛物线过原点;
③c<0?交点在y轴负半轴上.
(3)代数式-决定抛物线对称轴的位置
①ab>0?对称轴在y轴的左侧;
②b=0?对称轴是y轴;
③ab<0?对称轴在y轴的右侧.
(4)代数式b2-4ac决定抛物线与x轴交点的情况
①b2-4ac>0?抛物线与x轴有两个交点;
②b2-4ac=0?抛物线与x轴有一个交点;
③b2-4ac<0?抛物线与x轴没有交点.
【例】如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有 ( )
A.2个 B.3个 C.4个 D.1个
【标准解答】选D.图象与x轴有两个交点,得(1)正确;
图象与y轴交点在点(0,1)下方得c<1,所以(2)错误;
对称轴x=-在点(-1,0)右侧,得->-1并考虑a<0,去分母得-b<-2a,2a-b<0,所以(3)正确;
a+b+c是x=1时的函数值,从图象上看,横坐标为1时图象上的点在x轴下方,故a+b+c<0,所以(4)正确.综上只有一条信息错误.
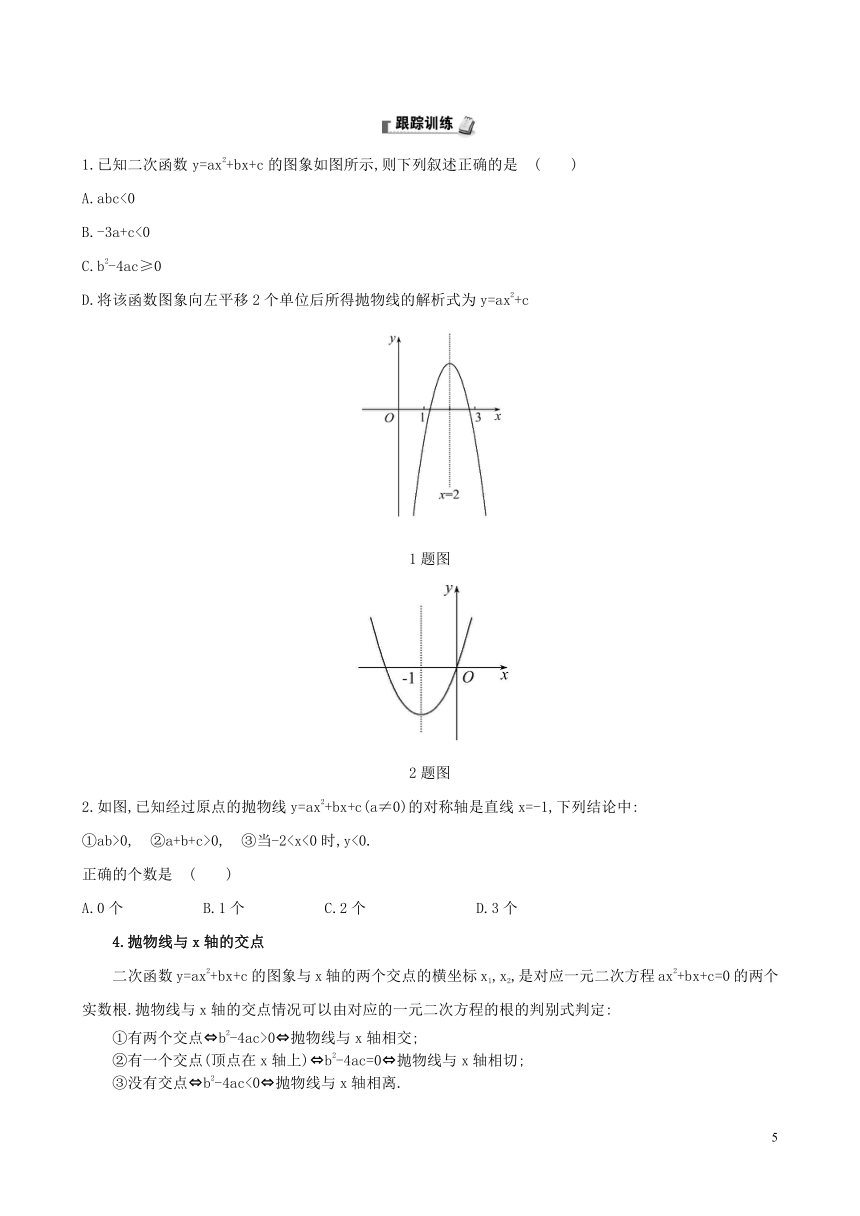
1.已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是 ( )
A.abc<0
B.-3a+c<0
C.b2-4ac≥0
D.将该函数图象向左平移2个单位后所得抛物线的解析式为y=ax2+c
1题图
2题图
2.如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:
①ab>0, ②a+b+c>0, ③当-2正确的个数是 ( )
A.0个 B.1个 C.2个 D.3个
4.抛物线与x轴的交点
二次函数y=ax2+bx+c的图象与x轴的两个交点的横坐标x1,x2,是对应一元二次方程ax2+bx+c=0的两个实数根.抛物线与x轴的交点情况可以由对应的一元二次方程的根的判别式判定:
①有两个交点?b2-4ac>0?抛物线与x轴相交;
②有一个交点(顶点在x轴上)?b2-4ac=0?抛物线与x轴相切;
③没有交点?b2-4ac<0?抛物线与x轴相离.
【例】已知抛物线y=-x2+mx-m+2.
(1)若抛物线与x轴的两个交点A,B分别在原点的两侧,并且AB=,试求m的值.
(2)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M,N,并且△MNC的面积等于27,试求m的值.
【标准解答】(1)设A(x1,0),B(x2,0),则x1,x2是方程x2-mx+m-2=0的两根.
∴x1+x2=m,x1·x2=m-2<0即m<2;
又AB=∣x1-x2∣=
=,∴m2-4m+3=0.
解得:m=1或m=3(舍去),
∴m的值为1.
(2)设M(a,b),则N(-a,-b).
∵M,N是抛物线上的两点,
∴
①+②得:-2a2-2m+4=0.
∴a2=-m+2.
∴当m<2时,才存在满足条件中的两点M,N.∴a=±.
这时M,N到y轴的距离均为,
又点C坐标为(0,2-m),而S△MNC=27,
∴2××(2-m)×=27.
∴解得m=-7.
1.如图是二次函数y=ax2+bx+c的图象,下列结论:
①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为-2;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.4个
1题图
2题图
2.如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是 .
3.已知抛物线的表达式为y=-x2+6x+c.
(1)若抛物线与x轴有交点,求c的取值范围.
(2)设抛物线与x轴两个交点的横坐标分别为x1,x2,若+=26,求c的值.
(3)若P,Q是抛物线上位于第一象限的不同两点,PA,QB都垂直于x轴,垂足分别为A,B,且△OPA与△OQB全等,求证:c>-.
5.二次函数解决实际问题时的方法
思考问题的基本思路是:
(1)理解问题.
(2)分析问题中的变量和常量.
(3)用函数表达式表示出它们之间的关系.
(4)利用二次函数的有关性质进行求解.
(5)检验结果的合理性,对问题加以拓展等.
【例】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量.
(2)求出y与x的函数关系式(不要求写出x的取值范围).
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
【标准解答】(1)45+×7.5=60(吨).
(2)y=(x-100),化简得:y=-x2+315x-24000.
(3)y=-x2+315x-24000=-(x-210)2+9075.
利达经销店要获得最大月利润,材料的售价应定为每吨210元.
(4)小静说的不对.理由:当月利润最大时,x为210元,而对于月销售额W=x=-(x-160)2+19200来说,当x为160元时,月销售额W最大.
∴当x为210元时,月销售额W不是最大.∴小静说的不对.
1.某广告公司要为客户设计一幅周长为12m的矩形广告牌,广告牌的设计费为每平方米1000元.
请你设计一个广告牌边长的方案,使得根据这个方案所确定的广告牌的长和宽能使获得的设计费最多,设计费最多为多少元?
2.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如表:
售价(元/件)
100
110
120
130
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件.(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
6.抛物线上是否存在点的探究方法
(1)虚拟检验法:欲探究抛物线是否存在满足条件A,B的点,先虚拟出符合条件A的点,然后再检验点是否满足条件B.满足即存在,反之不存在.
(2)分类探究法:欲探究抛物线上符合某条件的P点是否存在,可借助图形特殊点位置进行分类讨论.
(3)求解探索法:欲探索抛物线上满足条件A,B的点P是否存在,根据条件A,B列出关于P点坐标的方程(组),有解则存在,反之则不存在.
【例】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(-2,),顶点坐标为N,且与x轴交于A,B两点,与y轴交于C点.
(1)求抛物线的解析式.
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标.
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
【标准解答】(1)由抛物线顶点坐标为N,可设其解析式为y=a(x+1)2+,
将M(-2,)代入,得=a(-2+1)2+,解得a=-,
故所求抛物线的解析式为
y=-x2-x+.
(2)∵y=-x2-x+,
∴x=0时,y=,∴C(0,).
y=0时,-x2-x+=0,解得x=1或x=-3,
∴A(1,0),B(-3,0),
∴BC==2.
设P(-1,m),显然PB≠PC,所以
当CP=CB时,有CP==2,解得m=±;
当BP=BC时,有BP==2,解得m=±2.
综上,当△PBC为等腰三角形时,点P的坐标为(-1,+),(-1,-),(-1,2),(-1,-2).
(3)由(2)知BC=2,AC=2,AB=4,
所以BC2+AC2=AB2,即BC⊥AC.
连接BC并延长至B',使B'C=BC,连接B'M,交直线AC于点Q,
∵B,B'关于直线AC对称,
∴QB=QB',
∴QB+QM=QB'+QM=MB',
又BM=2,所以此时△QBM的周长最小.
由B(-3,0),C(0,),易得B'(3,2).
设直线MB'的解析式为y=kx+n,
将M(-2,),B'(3,2)代入,得解得
即直线MB'的解析式为y=x+.
同理可求得直线AC的解析式为
y=-x+.
由解得
即Q,
所以在直线AC上存在一点
Q,使△QBM的周长最小.
1.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A和B(4,m),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式.
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由.
(3)求△PAC为直角三角形时点P的坐标.
2.如图1,关于x的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
(1)求抛物线的解析式.
(2)DE上是否存在点P到AD的距离与到x轴的距离相等,若存在求出点P,若不存在,请说明理由.
(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC,若存在,求出点F的坐标,若不存在,请说明理由.
跟踪训练答案解析
1.二次函数y=ax2+bx+c的配方步骤
【跟踪训练】
1.【解析】选C.y=-x2+2x+4=-(x-1)2+5,所以当x=1时,取得最大值5.
2.【解析】y=x2-4x+5=x2-4x+4-4+5=(x-2)2+1.
答案:(x-2)2+1
3.【解析】∵y=x2+2x=(x+1)2-1,
∴二次函数y=x2+2x的顶点坐标是:(-1,-1),对称轴是直线x=-1.
答案:(-1,-1) x=-1
2.确定二次函数解析式的方法
【跟踪训练】
1.【解析】选C.因为此抛物线的顶点为(0,1),向右平移1个单位,再向上平移1个单位长度后的顶点为(1,2),所以所得抛物线为y=-2(x-1)2+2.
2.【解析】因为抛物线y=x2的图象向上平移1个单位,根据图象移动与关系式的变化规律可得y=x2+1.
答案:y=x2+1
3.【解析】∵点C在直线x=2上,且到抛物线的对称轴的距离等于1,
∴抛物线的对称轴为直线x=1或x=3,
当对称轴为直线x=1时,设抛物线解析式为y=a(x-1)2+k,
则解得
所以,y=(x-1)2+=x2-x+2,
当对称轴为直线x=3时,设抛物线解析式为y=a(x-3)2+k,
则解得
所以,y=-(x-3)2+=-x2+x+2,
综上所述,抛物线的函数解析式为
y=x2-x+2或y=-x2+x+2.
答案:y=x2-x+2或y=-x2+x+2
4.【解析】设二次函数的解析式为y=ax2+bx+c,把(0,49),(1,46),(4,25)代入函数解析式可得解得
∴函数的解析式为y=-x2-2x+49.
此函数的解析式的顶点横坐标-1即为最适合的温度.
答案:-1
3.二次函数y=ax2+bx+c中的系数值对抛物线的影响
【跟踪训练】
1.【解析】选B.A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0,故本选项错误;B.根据图知对称轴为直线x=2,即-=2,得b=-4a,再根据图象知当x=1时,y=a+b+c=a-4a+c=-3a+c<0,故本选项正确;C.由抛物线与x轴有两个交点,可得b2-4ac>0,故本选项错误;D.y=ax2+bx+c=a+,
∵-=2,∴原式=a(x-2)2+,向左平移2个单位后所得到抛物线的解析式为y=ax2+,故本选项错误.
2.【解析】选D.①∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴的左侧,∴b>0
∴ab>0,故①正确;
②∵观察图象知,
当x=1时y=a+b+c>0,∴②正确;
③∵抛物线的对称轴为x=-1,与x轴交于(0,0),∴另一个交点为(-2,0),
∴当-24.抛物线与x轴的交点
【跟踪训练】
1.【解析】选C.∵抛物线的顶点坐标为(-1,4),
∴二次三项式ax2+bx+c的最大值为4,①正确;
∵x=2时,y<0,∴4a+2b+c<0,②正确;
根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为-2,③正确;
使y≤3成立的x的取值范围是x≥0或x≤-2,④不正确.
2.【解析】因为点A(-1,0),B(3,0)在二次函数y=ax2+bx+3的图象上,
所以有解得
所以一元二次方程ax2+bx=0为-x2+2x=0.解得x1=0,x2=2.
答案:x1=0,x2=2
3.【解析】(1)利用二次函数与一元二次方程的关系,直接用判别式解答.
∵y=-x2+6x+c与x轴有交点,
∴-x2+6x+c=0有实数根,
∴Δ=b2-4ac≥0,
即62-4×(-1)×c≥0,解得c≥-9.
(2)∵-x2+6x+c=0有解,
且+=26,
∴c≥-9,(x1+x2)2-2x1x2=26,
即-2×=26,解得c=-5.
(3)设P的坐标为(m,n),则Q点坐标为(n,m),且m>0,n>0,m≠n,
将这两个点的坐标代入函数表达式得
①-②得:n2-m2+7(m-n)=0,
(n-m)(m+n-7)=0,
故可得:m+n=7,故可得n=7-m,
代入方程②得:-m2+7m+(c-7)=0.
因为存在这样的点,所以上述方程有解,所以判别式b2-4ac≥0,
即72-4×(-1)×(c-7)≥0,故c≥-.
而当c=-时,m=,此时n=,
故c>-.
5.二次函数解决实际问题时的方法
【跟踪训练】
1.【解析】设矩形一边长为xm,面积为Sm2,则另一边长为m,
则其面积S=x·=x(6-x)=-x2+6x,∵0<2x<12,∴0∵S=-x2+6x=-(x-3)2+9,
∴a=-1<0,S有最大值,
当x=3时,S最大值=9,
∴设计费最多为9×1000=9000(元),此时广告牌为正方形,边长为3m.
2.【解析】(1)①销售该运动服每件的利润是(x-60)元;
②设月销量W与x的关系式为W=kx+b,
由题意得,解得
∴W=-2x+400.
(2)由题意得,y=(x-60)(-2x+400)
=-2x2+520x-24000
=-2(x-130)2+9800,
∴售价为130元时,当月的利润最大,最大利润是9800元.
6.抛物线上是否存在点的探究方法
【跟踪训练】
1.【解析】(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,∴B(4,6),
∵A,B(4,6)在抛物线y=ax2+bx+6上,
∴
∴a=2,b=-8,∴y=2x2-8x+6.
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6),
=-2n2+9n-4=-2+,
∵PC>0,∴当n=时,线段PC最大且为.
(3)∵△PAC为直角三角形,
(i)若点P为直角顶点,则∠APC=90°,
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
(ii)若点A为直角顶点,则∠PAC=90°,
如图1,过点A作AN⊥x轴于点N,则ON=,AN=,过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0),
设直线AM的解析式为:y=kx+b,
则:解得
∴直线AM的解析式为:y=-x+3①,
又抛物线的解析式为:y=2x2-8x+6②,
联立①②式,解得:x=3或x=(与点A重合,舍去),∴C(3,0),即点C,M重合.
当x=3时,y=x+2=5.∴P1(3,5).
(ⅲ)若点C为直角顶点,则∠ACP=90°.
∵y=2x2-8x+6=2(x-2)2-2,
∴抛物线的对称轴为直线x=2,
如图2,作点A关于对称轴x=2的对称点C,
则点C在抛物线上,且C.
当x=时,y=x+2=,∴P2.
∵点P1(3,5),P2均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或.
2.【解析】(1)将A(-3,0),C(0,3)代入y=-x2+bx+c得:
解得:∴y=-x2-2x+3.
(2)存在.
当点P在∠DAB的角平分线上时,作PM⊥AD,设P(-1,y0),则PM=PD·sin∠ADE=(4-y0),PE=y0,
∵PM=PE,∴(4-y0)=y0,
解得:y0=-1,
当点P在∠DAB的外角平分线上时,作PN⊥AD,设P(-1,y0),
则PN=PD·sin∠ADE=(4-y0),
PE=-y0,
∵PN=PE,∴(4-y0)=-y0,
解得:y0=--1,
∴点P的坐标为P1(-1,-1),P2(-1,--1).
(3)S△EBC=3又2S△BCF=3S△EBC,
∴S△BCF=,
过F作FQ⊥x轴交BC的延长线于Q,
则S△FBC=S△FBQ-S△FCQ=FQ·OB=
∵BC的解析式为:y=-3x+3,
设F(x0,--2x0+3)则Q(x0,-3x0+3)
∴-3x0+3++2x0-3=9,
∴-x0-9=0,
∴x0=,,
∴点F的坐标为.
1.二次函数y=ax2+bx+c的配方步骤
(1)提:提取二次项系数,把二次项系数化为1.
(2)配:把括号内配成完全平方公式.
(3)化:把函数关系式化成顶点式.
【例】配方:y=4x2-8x.
【标准解答】y=4x2-8x =4(x2-2x)
=4(x2-2x+1-1)=4(x-1)2-4.
1.二次函数y=-x2+2x+4的最大值为( )
A.3 B.4 C.5 D.6
2.将二次函数y=x2-4x+5化为y=(x-h)2+k的形式,则y= .
3.二次函数y=x2+2x的顶点坐标为 ,对称轴是直线 .
2.确定二次函数解析式的方法
(1)一般式:若已知条件是图象上的三点,则用y=ax2+bx+c,将已知三个点的坐标代入,求出a,b,c的值.
【例1】已知二次函数的图象经过(0,1),(2,1)和(3,4),求该二次函数的解析式.
【标准解答】设函数解析式为y=ax2+bx+c,
则解得
∴y=x2-2x+1.
(2)顶点式:若已知二次函数图象的顶点坐标或对称轴方程与最大值(或最小值),设所求二次函数为y=a(x-h)2+k,将已知条件代入,求出待定系数.
【例2】根据函数图象写出二次函数的解析式.
【标准解答】由图象知抛物线对称轴x=-1,顶点坐标为(-1,2),过原点(0,0),点(-2,0).
设解析式为y=a(x+1)2+2,
∵过原点(0,0),∴a+2=0,a=-2.
故解析式为y=-2(x+1)2+2,即y=-2x2-4x.
(3)交点式:若已知二次函数图象与x轴的两个交点的坐标为(x1,0),(x2,0),设所求二次函数为y=a(x-x1)(x-x2),将第三点(m,n)的坐标(其中m,n为已知数)或其他已知条件代入,求出待定系数a.
【例3】已知函数y=ax2+bx+c的图象如图,那么函数解析式为 ( )
A.y=-x2+2x+3
B.y=x2-2x-3
C.y=-x2-2x+3
D.y=-x2-2x-3
【标准解答】选A.运用二次函数交点式:y=a(x-x1)(x-x2),则y=a(x+1)(x-3),把(0,3)代入,则a=-1,整理,得y=-x2+2x+3.
(4)根据平移确定解析式:先把抛物线化成顶点式y=a(x-h)2+k,然后根据h值左加右减,k值上加下减来进行.
【例4】抛物线y=(x+2)2-3可以由抛物线y=x2平移得到,则下列平移过程正确的是 ( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
【标准解答】选B.y=(x+2)2-3的顶点为(-2,-3),抛物线y=x2的顶点为(0,0),所以平移的过程是先向左平移2个单位,再向下平移3个单位.
1.将抛物线y=-2x2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为 ( )
A.y=-2(x+1)2
B.y=-2(x+1)2+2
C.y=-2(x-1)2+2
D.y=-2(x-1)2+1
2.将抛物线y=x2的图象向上平移1个单位,则平移后的抛物线的解析式为 .
3.设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 .
4.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:
温度t/℃
-4
-2
0
1
4
植物高度增
长量l/mm
41
49
49
46
25
经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为 ℃.
3.二次函数y=ax2+bx+c中的系数值对抛物线的影响
二次函数y=ax2+bx+c的图象特征与a,b,c的符号有密切联系,它们的关系如下:
(1)二次项系数a决定抛物线的开口方向、函数最值情况.
①a>0?开口向上,函数有最小值;
②a<0?开口向下,函数有最大值.
(2)常数项c决定抛物线与y轴的交点,交点坐标为(0,c).
①c>0?交点在y轴正半轴上;
②c=0?抛物线过原点;
③c<0?交点在y轴负半轴上.
(3)代数式-决定抛物线对称轴的位置
①ab>0?对称轴在y轴的左侧;
②b=0?对称轴是y轴;
③ab<0?对称轴在y轴的右侧.
(4)代数式b2-4ac决定抛物线与x轴交点的情况
①b2-4ac>0?抛物线与x轴有两个交点;
②b2-4ac=0?抛物线与x轴有一个交点;
③b2-4ac<0?抛物线与x轴没有交点.
【例】如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有 ( )
A.2个 B.3个 C.4个 D.1个
【标准解答】选D.图象与x轴有两个交点,得(1)正确;
图象与y轴交点在点(0,1)下方得c<1,所以(2)错误;
对称轴x=-在点(-1,0)右侧,得->-1并考虑a<0,去分母得-b<-2a,2a-b<0,所以(3)正确;
a+b+c是x=1时的函数值,从图象上看,横坐标为1时图象上的点在x轴下方,故a+b+c<0,所以(4)正确.综上只有一条信息错误.
1.已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是 ( )
A.abc<0
B.-3a+c<0
C.b2-4ac≥0
D.将该函数图象向左平移2个单位后所得抛物线的解析式为y=ax2+c
1题图
2题图
2.如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:
①ab>0, ②a+b+c>0, ③当-2
A.0个 B.1个 C.2个 D.3个
4.抛物线与x轴的交点
二次函数y=ax2+bx+c的图象与x轴的两个交点的横坐标x1,x2,是对应一元二次方程ax2+bx+c=0的两个实数根.抛物线与x轴的交点情况可以由对应的一元二次方程的根的判别式判定:
①有两个交点?b2-4ac>0?抛物线与x轴相交;
②有一个交点(顶点在x轴上)?b2-4ac=0?抛物线与x轴相切;
③没有交点?b2-4ac<0?抛物线与x轴相离.
【例】已知抛物线y=-x2+mx-m+2.
(1)若抛物线与x轴的两个交点A,B分别在原点的两侧,并且AB=,试求m的值.
(2)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M,N,并且△MNC的面积等于27,试求m的值.
【标准解答】(1)设A(x1,0),B(x2,0),则x1,x2是方程x2-mx+m-2=0的两根.
∴x1+x2=m,x1·x2=m-2<0即m<2;
又AB=∣x1-x2∣=
=,∴m2-4m+3=0.
解得:m=1或m=3(舍去),
∴m的值为1.
(2)设M(a,b),则N(-a,-b).
∵M,N是抛物线上的两点,
∴
①+②得:-2a2-2m+4=0.
∴a2=-m+2.
∴当m<2时,才存在满足条件中的两点M,N.∴a=±.
这时M,N到y轴的距离均为,
又点C坐标为(0,2-m),而S△MNC=27,
∴2××(2-m)×=27.
∴解得m=-7.
1.如图是二次函数y=ax2+bx+c的图象,下列结论:
①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为-2;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.4个
1题图
2题图
2.如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是 .
3.已知抛物线的表达式为y=-x2+6x+c.
(1)若抛物线与x轴有交点,求c的取值范围.
(2)设抛物线与x轴两个交点的横坐标分别为x1,x2,若+=26,求c的值.
(3)若P,Q是抛物线上位于第一象限的不同两点,PA,QB都垂直于x轴,垂足分别为A,B,且△OPA与△OQB全等,求证:c>-.
5.二次函数解决实际问题时的方法
思考问题的基本思路是:
(1)理解问题.
(2)分析问题中的变量和常量.
(3)用函数表达式表示出它们之间的关系.
(4)利用二次函数的有关性质进行求解.
(5)检验结果的合理性,对问题加以拓展等.
【例】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量.
(2)求出y与x的函数关系式(不要求写出x的取值范围).
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
【标准解答】(1)45+×7.5=60(吨).
(2)y=(x-100),化简得:y=-x2+315x-24000.
(3)y=-x2+315x-24000=-(x-210)2+9075.
利达经销店要获得最大月利润,材料的售价应定为每吨210元.
(4)小静说的不对.理由:当月利润最大时,x为210元,而对于月销售额W=x=-(x-160)2+19200来说,当x为160元时,月销售额W最大.
∴当x为210元时,月销售额W不是最大.∴小静说的不对.
1.某广告公司要为客户设计一幅周长为12m的矩形广告牌,广告牌的设计费为每平方米1000元.
请你设计一个广告牌边长的方案,使得根据这个方案所确定的广告牌的长和宽能使获得的设计费最多,设计费最多为多少元?
2.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如表:
售价(元/件)
100
110
120
130
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件.(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
6.抛物线上是否存在点的探究方法
(1)虚拟检验法:欲探究抛物线是否存在满足条件A,B的点,先虚拟出符合条件A的点,然后再检验点是否满足条件B.满足即存在,反之不存在.
(2)分类探究法:欲探究抛物线上符合某条件的P点是否存在,可借助图形特殊点位置进行分类讨论.
(3)求解探索法:欲探索抛物线上满足条件A,B的点P是否存在,根据条件A,B列出关于P点坐标的方程(组),有解则存在,反之则不存在.
【例】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(-2,),顶点坐标为N,且与x轴交于A,B两点,与y轴交于C点.
(1)求抛物线的解析式.
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标.
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
【标准解答】(1)由抛物线顶点坐标为N,可设其解析式为y=a(x+1)2+,
将M(-2,)代入,得=a(-2+1)2+,解得a=-,
故所求抛物线的解析式为
y=-x2-x+.
(2)∵y=-x2-x+,
∴x=0时,y=,∴C(0,).
y=0时,-x2-x+=0,解得x=1或x=-3,
∴A(1,0),B(-3,0),
∴BC==2.
设P(-1,m),显然PB≠PC,所以
当CP=CB时,有CP==2,解得m=±;
当BP=BC时,有BP==2,解得m=±2.
综上,当△PBC为等腰三角形时,点P的坐标为(-1,+),(-1,-),(-1,2),(-1,-2).
(3)由(2)知BC=2,AC=2,AB=4,
所以BC2+AC2=AB2,即BC⊥AC.
连接BC并延长至B',使B'C=BC,连接B'M,交直线AC于点Q,
∵B,B'关于直线AC对称,
∴QB=QB',
∴QB+QM=QB'+QM=MB',
又BM=2,所以此时△QBM的周长最小.
由B(-3,0),C(0,),易得B'(3,2).
设直线MB'的解析式为y=kx+n,
将M(-2,),B'(3,2)代入,得解得
即直线MB'的解析式为y=x+.
同理可求得直线AC的解析式为
y=-x+.
由解得
即Q,
所以在直线AC上存在一点
Q,使△QBM的周长最小.
1.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A和B(4,m),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式.
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由.
(3)求△PAC为直角三角形时点P的坐标.
2.如图1,关于x的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
(1)求抛物线的解析式.
(2)DE上是否存在点P到AD的距离与到x轴的距离相等,若存在求出点P,若不存在,请说明理由.
(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC,若存在,求出点F的坐标,若不存在,请说明理由.
跟踪训练答案解析
1.二次函数y=ax2+bx+c的配方步骤
【跟踪训练】
1.【解析】选C.y=-x2+2x+4=-(x-1)2+5,所以当x=1时,取得最大值5.
2.【解析】y=x2-4x+5=x2-4x+4-4+5=(x-2)2+1.
答案:(x-2)2+1
3.【解析】∵y=x2+2x=(x+1)2-1,
∴二次函数y=x2+2x的顶点坐标是:(-1,-1),对称轴是直线x=-1.
答案:(-1,-1) x=-1
2.确定二次函数解析式的方法
【跟踪训练】
1.【解析】选C.因为此抛物线的顶点为(0,1),向右平移1个单位,再向上平移1个单位长度后的顶点为(1,2),所以所得抛物线为y=-2(x-1)2+2.
2.【解析】因为抛物线y=x2的图象向上平移1个单位,根据图象移动与关系式的变化规律可得y=x2+1.
答案:y=x2+1
3.【解析】∵点C在直线x=2上,且到抛物线的对称轴的距离等于1,
∴抛物线的对称轴为直线x=1或x=3,
当对称轴为直线x=1时,设抛物线解析式为y=a(x-1)2+k,
则解得
所以,y=(x-1)2+=x2-x+2,
当对称轴为直线x=3时,设抛物线解析式为y=a(x-3)2+k,
则解得
所以,y=-(x-3)2+=-x2+x+2,
综上所述,抛物线的函数解析式为
y=x2-x+2或y=-x2+x+2.
答案:y=x2-x+2或y=-x2+x+2
4.【解析】设二次函数的解析式为y=ax2+bx+c,把(0,49),(1,46),(4,25)代入函数解析式可得解得
∴函数的解析式为y=-x2-2x+49.
此函数的解析式的顶点横坐标-1即为最适合的温度.
答案:-1
3.二次函数y=ax2+bx+c中的系数值对抛物线的影响
【跟踪训练】
1.【解析】选B.A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0,故本选项错误;B.根据图知对称轴为直线x=2,即-=2,得b=-4a,再根据图象知当x=1时,y=a+b+c=a-4a+c=-3a+c<0,故本选项正确;C.由抛物线与x轴有两个交点,可得b2-4ac>0,故本选项错误;D.y=ax2+bx+c=a+,
∵-=2,∴原式=a(x-2)2+,向左平移2个单位后所得到抛物线的解析式为y=ax2+,故本选项错误.
2.【解析】选D.①∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴的左侧,∴b>0
∴ab>0,故①正确;
②∵观察图象知,
当x=1时y=a+b+c>0,∴②正确;
③∵抛物线的对称轴为x=-1,与x轴交于(0,0),∴另一个交点为(-2,0),
∴当-2
【跟踪训练】
1.【解析】选C.∵抛物线的顶点坐标为(-1,4),
∴二次三项式ax2+bx+c的最大值为4,①正确;
∵x=2时,y<0,∴4a+2b+c<0,②正确;
根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为-2,③正确;
使y≤3成立的x的取值范围是x≥0或x≤-2,④不正确.
2.【解析】因为点A(-1,0),B(3,0)在二次函数y=ax2+bx+3的图象上,
所以有解得
所以一元二次方程ax2+bx=0为-x2+2x=0.解得x1=0,x2=2.
答案:x1=0,x2=2
3.【解析】(1)利用二次函数与一元二次方程的关系,直接用判别式解答.
∵y=-x2+6x+c与x轴有交点,
∴-x2+6x+c=0有实数根,
∴Δ=b2-4ac≥0,
即62-4×(-1)×c≥0,解得c≥-9.
(2)∵-x2+6x+c=0有解,
且+=26,
∴c≥-9,(x1+x2)2-2x1x2=26,
即-2×=26,解得c=-5.
(3)设P的坐标为(m,n),则Q点坐标为(n,m),且m>0,n>0,m≠n,
将这两个点的坐标代入函数表达式得
①-②得:n2-m2+7(m-n)=0,
(n-m)(m+n-7)=0,
故可得:m+n=7,故可得n=7-m,
代入方程②得:-m2+7m+(c-7)=0.
因为存在这样的点,所以上述方程有解,所以判别式b2-4ac≥0,
即72-4×(-1)×(c-7)≥0,故c≥-.
而当c=-时,m=,此时n=,
故c>-.
5.二次函数解决实际问题时的方法
【跟踪训练】
1.【解析】设矩形一边长为xm,面积为Sm2,则另一边长为m,
则其面积S=x·=x(6-x)=-x2+6x,∵0<2x<12,∴0
∴a=-1<0,S有最大值,
当x=3时,S最大值=9,
∴设计费最多为9×1000=9000(元),此时广告牌为正方形,边长为3m.
2.【解析】(1)①销售该运动服每件的利润是(x-60)元;
②设月销量W与x的关系式为W=kx+b,
由题意得,解得
∴W=-2x+400.
(2)由题意得,y=(x-60)(-2x+400)
=-2x2+520x-24000
=-2(x-130)2+9800,
∴售价为130元时,当月的利润最大,最大利润是9800元.
6.抛物线上是否存在点的探究方法
【跟踪训练】
1.【解析】(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,∴B(4,6),
∵A,B(4,6)在抛物线y=ax2+bx+6上,
∴
∴a=2,b=-8,∴y=2x2-8x+6.
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6),
=-2n2+9n-4=-2+,
∵PC>0,∴当n=时,线段PC最大且为.
(3)∵△PAC为直角三角形,
(i)若点P为直角顶点,则∠APC=90°,
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
(ii)若点A为直角顶点,则∠PAC=90°,
如图1,过点A作AN⊥x轴于点N,则ON=,AN=,过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0),
设直线AM的解析式为:y=kx+b,
则:解得
∴直线AM的解析式为:y=-x+3①,
又抛物线的解析式为:y=2x2-8x+6②,
联立①②式,解得:x=3或x=(与点A重合,舍去),∴C(3,0),即点C,M重合.
当x=3时,y=x+2=5.∴P1(3,5).
(ⅲ)若点C为直角顶点,则∠ACP=90°.
∵y=2x2-8x+6=2(x-2)2-2,
∴抛物线的对称轴为直线x=2,
如图2,作点A关于对称轴x=2的对称点C,
则点C在抛物线上,且C.
当x=时,y=x+2=,∴P2.
∵点P1(3,5),P2均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或.
2.【解析】(1)将A(-3,0),C(0,3)代入y=-x2+bx+c得:
解得:∴y=-x2-2x+3.
(2)存在.
当点P在∠DAB的角平分线上时,作PM⊥AD,设P(-1,y0),则PM=PD·sin∠ADE=(4-y0),PE=y0,
∵PM=PE,∴(4-y0)=y0,
解得:y0=-1,
当点P在∠DAB的外角平分线上时,作PN⊥AD,设P(-1,y0),
则PN=PD·sin∠ADE=(4-y0),
PE=-y0,
∵PN=PE,∴(4-y0)=-y0,
解得:y0=--1,
∴点P的坐标为P1(-1,-1),P2(-1,--1).
(3)S△EBC=3又2S△BCF=3S△EBC,
∴S△BCF=,
过F作FQ⊥x轴交BC的延长线于Q,
则S△FBC=S△FBQ-S△FCQ=FQ·OB=
∵BC的解析式为:y=-3x+3,
设F(x0,--2x0+3)则Q(x0,-3x0+3)
∴-3x0+3++2x0-3=9,
∴-x0-9=0,
∴x0=,,
∴点F的坐标为.
