六年级下册数学优秀课件4.4《反比例》北师大版(共22张PPT)
文档属性
| 名称 | 六年级下册数学优秀课件4.4《反比例》北师大版(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-06 00:00:00 | ||
图片预览








文档简介
课件22张PPT。反比例北师大版六年级数学下册说一说正比例的两个量的变化情况。1.两个相关联的量。
2.一个量增加,另一个量也随着增加,一个量减少,另一个量也随着减少。
3.两个量的比值相同。 1. 正比例关系用字母怎样表示? 2.判断下列量是否成正比例。 ①时间一定,行驶的路程和速度。 ②大米总量一定,吃了的和剩下的。 ③圆的周长和半径。学习目标
1.结合丰富的实例,认识反比例。
2.能根据反比例的意义,判断两个相关联量是否成反比例。
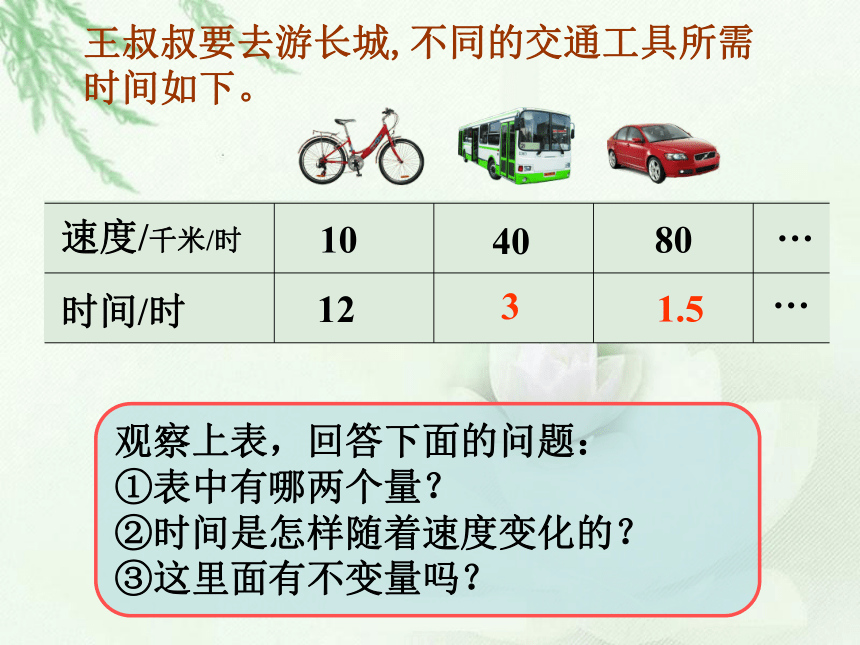
3.利用反比例解决一些简单的生活问题,感受反比例关系在生活中的广泛应用。王叔叔要去游长城,不同的交通工具所需时间如下。速度/千米/时时间/时1040801231.5……观察上表,回答下面的问题:
①表中有哪两个量?
②时间是怎样随着速度变化的?
③这里面有不变量吗?速度是10,时间是12;速度是40,时间是3;速度是80,时间是1.5;速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。速度增加,所需时间减少。速度减小,所需时间增多。对应的速度和所需时间的积总是一定的10×12=12040×3=12080×1.5=120(一定)速度×时间=路程有600毫升果汁,可平均分成若干杯。请把下表填完整分的杯数/杯每杯的果汁量/ml65432100…… 120150200300(1)表中有哪两种量?表中有每杯的果汁量和分的杯数两种量(2)分的杯数是怎样随着每杯的果汁量变化的?每杯的果汁量扩大,分的杯数反而缩小;每杯的果汁量缩小,分的杯数反而扩大;每杯的果汁量和分的杯数的积是一定的(3)它们的关系是什么?每杯的果汁量× 分的杯数= 果汁总量(一定)有600毫升果汁,可平均分成若干杯。请把下表填完整分的杯数/杯每杯的果汁量/ml65432100…… 12015200300 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。 X×y=k (一定) 反比例两个量的变化情况:1.两个相关联的量。
2.一个量增加,另一个量反而减少,一个量减少,另一个量反而增加。
3.两个量的乘积相同。达标训练当堂清 填一填
1.两种相关联的量,一种量变化,另一种量也随着( )(但是变化的方向相反),如果这两种量中相对应的两个数的积一定,这两种量就叫做( ),它们的关系叫做( )。
2.如果XY=K(一定),那么X和Y之间的关系是( )关系。
3.小明做12道数学题,做完的题和没做完的题( )比例。
每天的烧煤量(kg)20 40 50 100 烧煤的天数 50 25 20 101.下表中的两个量成反比例吗?为什么?课堂检测判断下面每题中的两种量是不是成反比例,并说明理由。判断下面每题中的两种量是不是成反比例,并说明理由。判断下面每题中的两种量是不是成反比例,并说明理由。判断下面每题中的两种量是不是成反比例,并说明理由。 想一想平均每天看的页数和看完全书所需天数有什么关系,并说明理由。 每天看的页数×所需天数=书本页数(一定)8643604030时间×速度=稿件字数(一定)在打同一份稿件的过程中,哪个量没有变化?
2.打字的速度和所用的时间有什么关系?
3.李老师打这份稿件用了24分钟,你知道她平均1分打多少字?稿件总字数速度快,所用时间少;速度慢,所用时间多。10分钟。思考:
1、表中有哪两种量?
2、所需的加工时间怎样随着每小时加工的个数变化?
3、每两个相对应的数的乘积各是多少?
( 工效、时间)(每小时加工零件的个数越多,所需的时间越少)( 600)工效×时间=工作总量(一定)课堂小结 这节课你有什么收获?课后作业
1.找一找生活中的反比例的例子。
2.预习下节课的学习内容《观察与探究》
2.一个量增加,另一个量也随着增加,一个量减少,另一个量也随着减少。
3.两个量的比值相同。 1. 正比例关系用字母怎样表示? 2.判断下列量是否成正比例。 ①时间一定,行驶的路程和速度。 ②大米总量一定,吃了的和剩下的。 ③圆的周长和半径。学习目标
1.结合丰富的实例,认识反比例。
2.能根据反比例的意义,判断两个相关联量是否成反比例。
3.利用反比例解决一些简单的生活问题,感受反比例关系在生活中的广泛应用。王叔叔要去游长城,不同的交通工具所需时间如下。速度/千米/时时间/时1040801231.5……观察上表,回答下面的问题:
①表中有哪两个量?
②时间是怎样随着速度变化的?
③这里面有不变量吗?速度是10,时间是12;速度是40,时间是3;速度是80,时间是1.5;速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。速度增加,所需时间减少。速度减小,所需时间增多。对应的速度和所需时间的积总是一定的10×12=12040×3=12080×1.5=120(一定)速度×时间=路程有600毫升果汁,可平均分成若干杯。请把下表填完整分的杯数/杯每杯的果汁量/ml65432100…… 120150200300(1)表中有哪两种量?表中有每杯的果汁量和分的杯数两种量(2)分的杯数是怎样随着每杯的果汁量变化的?每杯的果汁量扩大,分的杯数反而缩小;每杯的果汁量缩小,分的杯数反而扩大;每杯的果汁量和分的杯数的积是一定的(3)它们的关系是什么?每杯的果汁量× 分的杯数= 果汁总量(一定)有600毫升果汁,可平均分成若干杯。请把下表填完整分的杯数/杯每杯的果汁量/ml65432100…… 12015200300 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。 X×y=k (一定) 反比例两个量的变化情况:1.两个相关联的量。
2.一个量增加,另一个量反而减少,一个量减少,另一个量反而增加。
3.两个量的乘积相同。达标训练当堂清 填一填
1.两种相关联的量,一种量变化,另一种量也随着( )(但是变化的方向相反),如果这两种量中相对应的两个数的积一定,这两种量就叫做( ),它们的关系叫做( )。
2.如果XY=K(一定),那么X和Y之间的关系是( )关系。
3.小明做12道数学题,做完的题和没做完的题( )比例。
每天的烧煤量(kg)20 40 50 100 烧煤的天数 50 25 20 101.下表中的两个量成反比例吗?为什么?课堂检测判断下面每题中的两种量是不是成反比例,并说明理由。判断下面每题中的两种量是不是成反比例,并说明理由。判断下面每题中的两种量是不是成反比例,并说明理由。判断下面每题中的两种量是不是成反比例,并说明理由。 想一想平均每天看的页数和看完全书所需天数有什么关系,并说明理由。 每天看的页数×所需天数=书本页数(一定)8643604030时间×速度=稿件字数(一定)在打同一份稿件的过程中,哪个量没有变化?
2.打字的速度和所用的时间有什么关系?
3.李老师打这份稿件用了24分钟,你知道她平均1分打多少字?稿件总字数速度快,所用时间少;速度慢,所用时间多。10分钟。思考:
1、表中有哪两种量?
2、所需的加工时间怎样随着每小时加工的个数变化?
3、每两个相对应的数的乘积各是多少?
( 工效、时间)(每小时加工零件的个数越多,所需的时间越少)( 600)工效×时间=工作总量(一定)课堂小结 这节课你有什么收获?课后作业
1.找一找生活中的反比例的例子。
2.预习下节课的学习内容《观察与探究》
