人教版数学八年级下册 18.1.2 平行四边形的判定课件(共29张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2 平行四边形的判定课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 274.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-06 20:10:34 | ||
图片预览






文档简介
课件29张PPT。 新人教版八年级数学(下册) 思 考有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的亮亮拿着有三个顶点的碎片很快将原来的平行四边形画了出来。
你想知道他是如何做到的吗?平行四边形的判定(1)通过合作探究,得出平行四边形的判定方法;
(2)理解并能灵活运用平行四边形的判定方法解决实际问题。学习目标平行四边形判定方法的探究以及平行四边形的判定定理的灵活运用.对平行四边形判定方法猜想,验证以及平行四边形的性质和判定的综合运用. (强调:在求证四边形为平行四边形时用判定定理,在已知四边形是平行四边形时用性质定理)学习难点学习重点复习回顾两组对边分别平行的四边形叫做平行四边形.平行四边形的定义:性
质平行四边形的两组对边分别平行平行四边形的两组对边分别相等平行四边形的两组对角分别相等平行四边形的邻角互补平行四边形的对角线互相平分 学习了平行四边形后,小明回家用细木棒钉制了一个四边形。
第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请大家帮帮忙合作探究:探究一:小明拿着自己做的平行四边形自信的说:
因为我的四边形
AB∥CD 且 AD∥BC
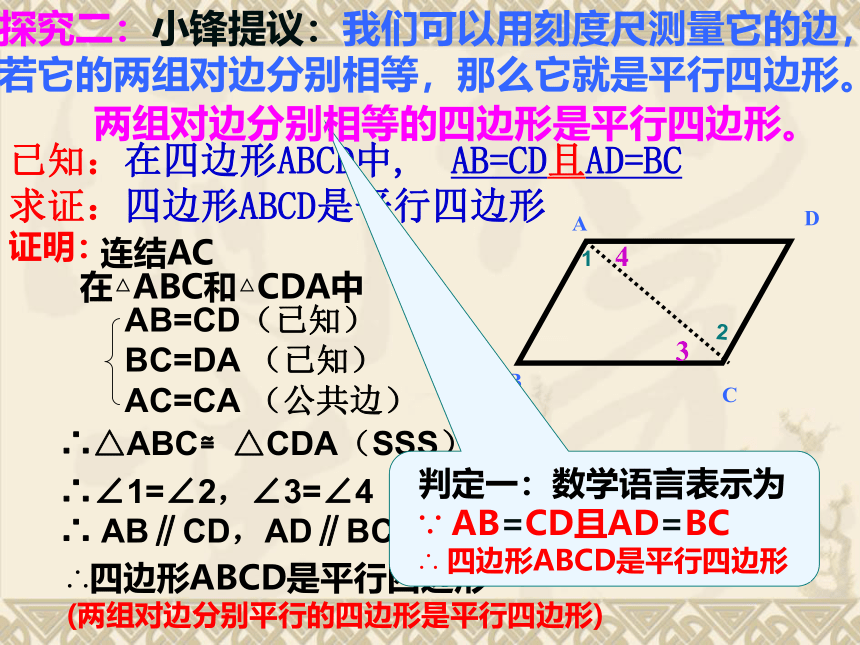
所以我做的四边形就是平行四边形。两组对边分别平行的四边形叫做平行四边形.定义法:已知:在四边形ABCD中, AB=CD且AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC34∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
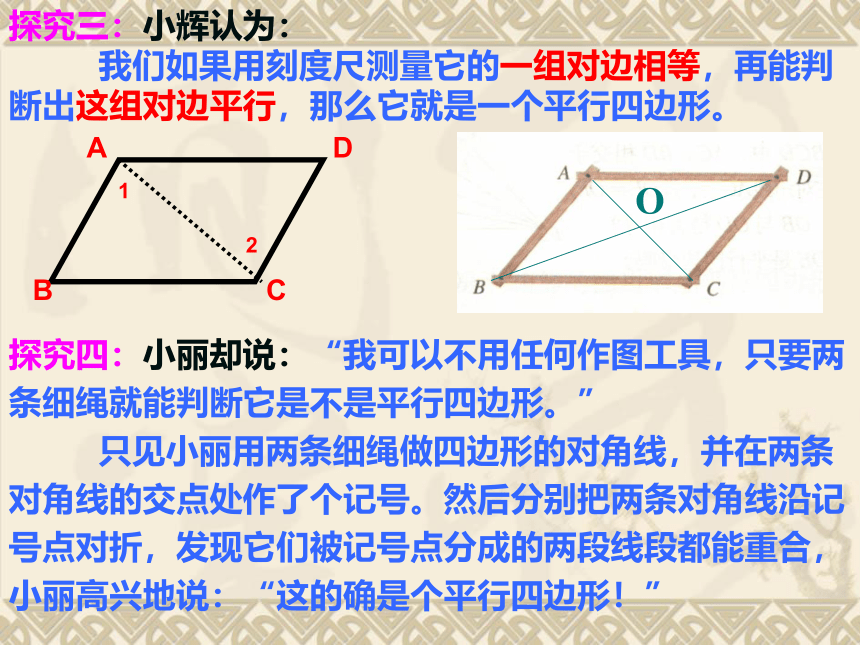
12探究二:小锋提议:我们可以用刻度尺测量它的边,若它的两组对边分别相等,那么它就是平行四边形。 两组对边分别相等的四边形是平行四边形。探究四:小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!” 1 2A B D CO探究三:小辉认为:
我们如果用刻度尺测量它的一组对边相等,再能判断出这组对边平行,那么它就是一个平行四边形。探究三:小辉认为:
我们如果用刻度尺测量它的一组对边相等,再能判断出这组对边平行,那么它就是一个平行四边形。12ABCD已知:在四边形ABCD中,
AB ∥ CD 且AB=CD
求证:四边形ABCD是平行四边形一组对边平行且相等的四边形是平行四边形。探究四:小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认同小丽的做法吗?已知:四边形对角线相交于点O,且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形
(两组对边分别相等的四 边形是平行四边形。)
对角线互相平分的四边形是平行四边形。快乐大比拼(1)如图(1),在四边形ABCD中,当AB∥CD时,四边形ABCD是平行四边形吗?依据是什么?如图(2),请判断四边形ABCD是平行四边形吗?依据是什么?
ADBC7.6㎝7.6㎝4.8㎝4.8㎝(2)快乐大比拼(3)快乐大比拼如图(3),请判断四边形ABCD是平行四边形吗?依据是什么?
2cm2cm(4)快乐大比拼如图(4),请判断四边形ABCD是平行四边形吗?依据是什么?
解决问题有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的亮亮拿着有三个顶点的碎片很快将原来的平行四边形画了出来。如果你只有两把没刻度的直尺和圆规,你能帮它补好吗?D依据:定义法定义:
∵ AB ∥ CD,AD ∥ BC
∴ 四边形ABCD是平行四边形方法一:方法二:D依据:判定一DOBAC方法三:依据:判定三例题分析例:如图,平行四边形ABCD的对角线AC,BD 相交于点O,E, F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形。ABCDEFO 谈谈你本节课的收获。
ABCD当堂检测:1.如图,若AB=8cm,AD=4cm,
那么BC= cm,CD= cm时,
四边形ABCD是平 行四边形。
BACDD2.如图,若AC=8 cm,BD=10cm,对角线AC,BD相交于点O,则AO= cm,DO= cm时,四边形ABCD为平行四边形。
ACBO3.如图,AB=DC=EF, AD=BC,DE=CF,
则图中有哪些互相平行的线段?
AFECDB课外拓展:1、如图,四边形ABCD中,BC∥AD , AE∥DC, AB=DC
求证:∠B=∠C.
EDCBA2、已知:如图,在四边形ABCD中,
AD∥BC, E, F为对角线AC上两点,且 AE=CF,DF∥BE.
求证:四边形ABCD是平行四边形.EFDCBA中考链接:
已知:在四边形ABCD中,AD∥BC, ∠A=∠C.
求证:四边形ABCD是平行四边形 .
DCBA作业布置思考:你同意他的观点吗?试证明。 小刚提议:我们可以度量它的角,如果它的
两组对角分别相等,那么它就是平行四边形。
你想知道他是如何做到的吗?平行四边形的判定(1)通过合作探究,得出平行四边形的判定方法;
(2)理解并能灵活运用平行四边形的判定方法解决实际问题。学习目标平行四边形判定方法的探究以及平行四边形的判定定理的灵活运用.对平行四边形判定方法猜想,验证以及平行四边形的性质和判定的综合运用. (强调:在求证四边形为平行四边形时用判定定理,在已知四边形是平行四边形时用性质定理)学习难点学习重点复习回顾两组对边分别平行的四边形叫做平行四边形.平行四边形的定义:性
质平行四边形的两组对边分别平行平行四边形的两组对边分别相等平行四边形的两组对角分别相等平行四边形的邻角互补平行四边形的对角线互相平分 学习了平行四边形后,小明回家用细木棒钉制了一个四边形。
第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请大家帮帮忙合作探究:探究一:小明拿着自己做的平行四边形自信的说:
因为我的四边形
AB∥CD 且 AD∥BC
所以我做的四边形就是平行四边形。两组对边分别平行的四边形叫做平行四边形.定义法:已知:在四边形ABCD中, AB=CD且AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC34∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
12探究二:小锋提议:我们可以用刻度尺测量它的边,若它的两组对边分别相等,那么它就是平行四边形。 两组对边分别相等的四边形是平行四边形。探究四:小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!” 1 2A B D CO探究三:小辉认为:
我们如果用刻度尺测量它的一组对边相等,再能判断出这组对边平行,那么它就是一个平行四边形。探究三:小辉认为:
我们如果用刻度尺测量它的一组对边相等,再能判断出这组对边平行,那么它就是一个平行四边形。12ABCD已知:在四边形ABCD中,
AB ∥ CD 且AB=CD
求证:四边形ABCD是平行四边形一组对边平行且相等的四边形是平行四边形。探究四:小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认同小丽的做法吗?已知:四边形对角线相交于点O,且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形
(两组对边分别相等的四 边形是平行四边形。)
对角线互相平分的四边形是平行四边形。快乐大比拼(1)如图(1),在四边形ABCD中,当AB∥CD时,四边形ABCD是平行四边形吗?依据是什么?如图(2),请判断四边形ABCD是平行四边形吗?依据是什么?
ADBC7.6㎝7.6㎝4.8㎝4.8㎝(2)快乐大比拼(3)快乐大比拼如图(3),请判断四边形ABCD是平行四边形吗?依据是什么?
2cm2cm(4)快乐大比拼如图(4),请判断四边形ABCD是平行四边形吗?依据是什么?
解决问题有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的亮亮拿着有三个顶点的碎片很快将原来的平行四边形画了出来。如果你只有两把没刻度的直尺和圆规,你能帮它补好吗?D依据:定义法定义:
∵ AB ∥ CD,AD ∥ BC
∴ 四边形ABCD是平行四边形方法一:方法二:D依据:判定一DOBAC方法三:依据:判定三例题分析例:如图,平行四边形ABCD的对角线AC,BD 相交于点O,E, F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形。ABCDEFO 谈谈你本节课的收获。
ABCD当堂检测:1.如图,若AB=8cm,AD=4cm,
那么BC= cm,CD= cm时,
四边形ABCD是平 行四边形。
BACDD2.如图,若AC=8 cm,BD=10cm,对角线AC,BD相交于点O,则AO= cm,DO= cm时,四边形ABCD为平行四边形。
ACBO3.如图,AB=DC=EF, AD=BC,DE=CF,
则图中有哪些互相平行的线段?
AFECDB课外拓展:1、如图,四边形ABCD中,BC∥AD , AE∥DC, AB=DC
求证:∠B=∠C.
EDCBA2、已知:如图,在四边形ABCD中,
AD∥BC, E, F为对角线AC上两点,且 AE=CF,DF∥BE.
求证:四边形ABCD是平行四边形.EFDCBA中考链接:
已知:在四边形ABCD中,AD∥BC, ∠A=∠C.
求证:四边形ABCD是平行四边形 .
DCBA作业布置思考:你同意他的观点吗?试证明。 小刚提议:我们可以度量它的角,如果它的
两组对角分别相等,那么它就是平行四边形。
