人教版数学八年级下册 18.1.2 平行四边形的判定课件(共28张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2 平行四边形的判定课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 435.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-06 20:22:28 | ||
图片预览



文档简介
课件28张PPT。18.1.2平行四边形的判定第一课时人教版数学八年级下册1. 掌握平行四边形判定定理,并会运用判定定理解决相关问题。
2. 探索两种组成平行四边形的方法,由此发现平行四边形的判定。
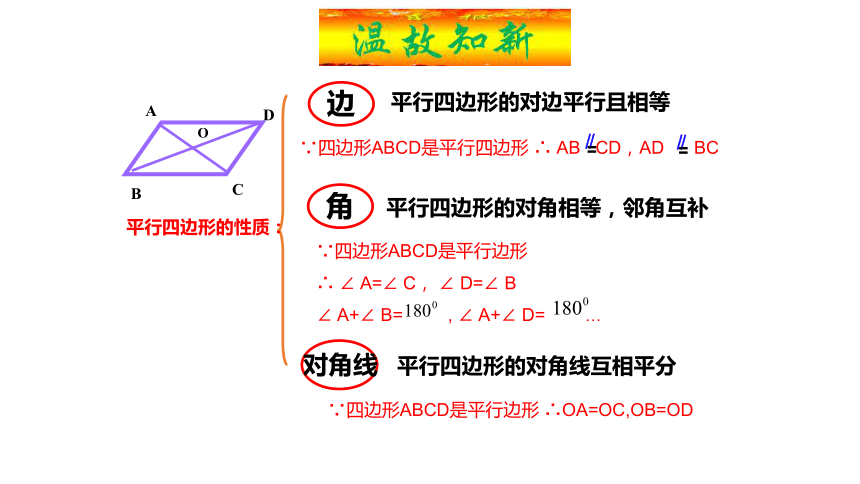
平行四边形的对边平行且相等 平行四边形的对角线互相平分平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD4 平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
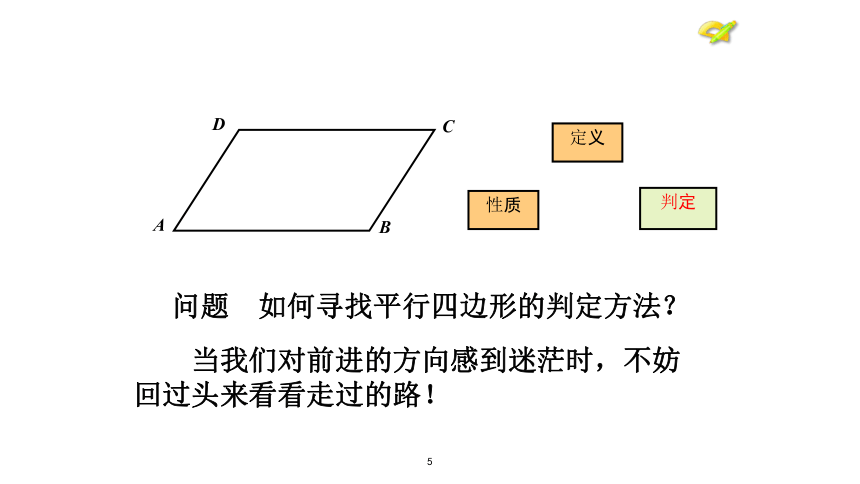
平行四边形的性质:对边相等,对角相等,对角线互相平分.?判定性质定义5判定性质定义 问题 如何寻找平行四边形的判定方法? 当我们对前进的方向感到迷茫时,不妨回过头来看看走过的路!6直角三角
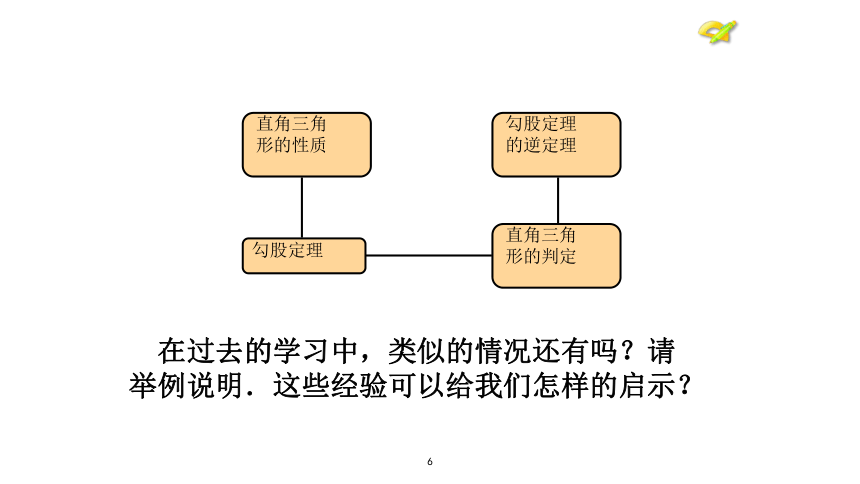
形的性质 直角三角
形的判定 勾股定理 勾股定理
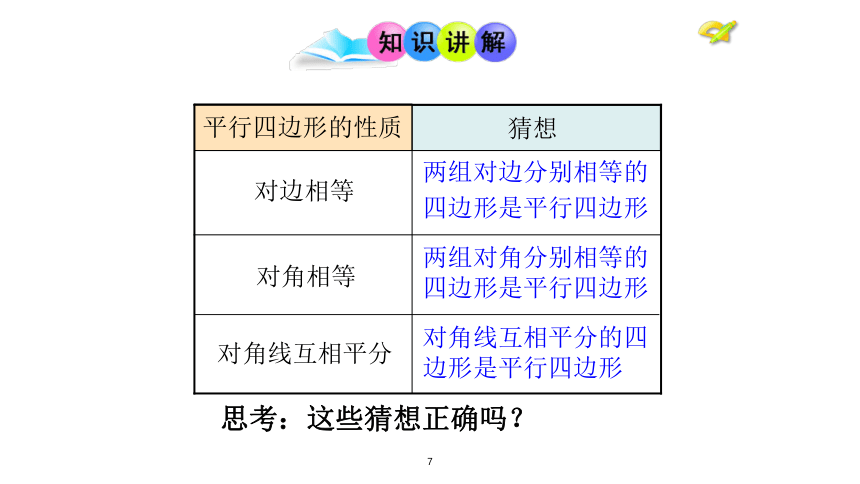
的逆定理 在过去的学习中,类似的情况还有吗?请举例说明.这些经验可以给我们怎样的启示?7两组对边分别相等的
四边形是平行四边形 两组对角分别相等的
四边形是平行四边形 对角线互相平分的四
边形是平行四边形 思考:这些猜想正确吗? 活动1 将两长两短的四根细木条用小钉 钉在一起,让相等的木条作为对边,做一个四边形。它是平行四边形吗?
命题1
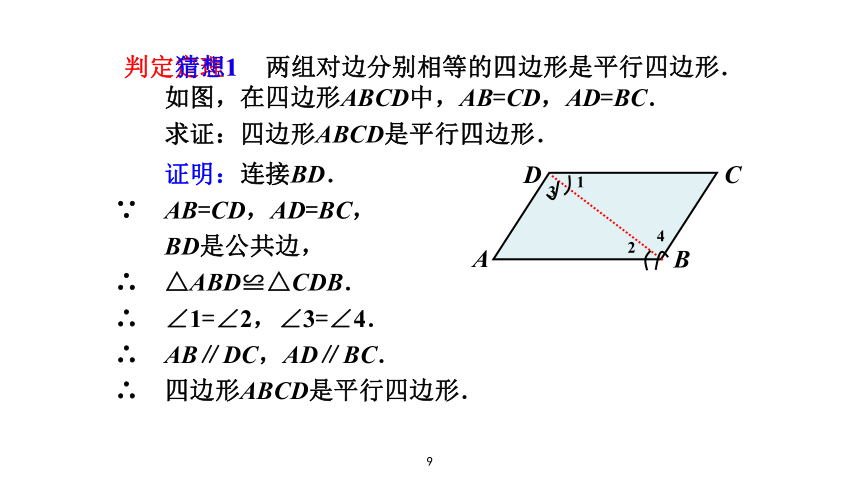
两组对边分别相等的四边形是平行四边形9 证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形. 两组对边分别相等的四边形是平行四边形. 判定定理1 猜想1 10 证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 两组对角分别相等的四边形是平行四边形. 判定定理2 猜想2 活动2 将两根细木条的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成的四边形是平行四边形吗?命题2 对角线互相平分的四边形是平行四边形12 如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形. 对角线互相平分的四边形是平行四边形. 判定定理3 猜想3 证明:∵ OA=OC,OB=OD,
∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.归纳两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;AD∥BC AB∥DCAD=BC AB=DC∠BAD=∠BCD ∠ABC=∠ADC四边形ABCD是平行四边形如图,用符号表示如下:平行四边形有哪些判定方法?对角线互相平分的四边形是平行四边形。OA=OC OB=OD两组对边分别相等的四边形是平行四边形;四边形ABCD是平行四边形四边形ABCD是平行四边形四边形ABCD是平行四边形判断下列四边形是否是平行四边形?并说明理由.BADC110°110°⑴⑶ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵70°15证明:
∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF. 例1 如图,AB=DC=EF,AD=BC,DE=CF.
求证:AB∥EF.图中还有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:17 例2 如图,平行四边形ABCD中,E,F分别是对角线AC 上的两点,并且 AE=CF.
求证:四边形BFDE是平行四边形.O ∴四边形DEBF是平行四边形;证明:
∵四边形ABCD是平行四边形, ∴AO=CO,BO=DO, ∴EO=FO, ∵AE=CF你还有其它的证法吗?18O 在上题中,若点E,F 分别在AC 两侧的延长线上,如图,其他条件不变,结论还成立吗?请证明你的结论. ∴四边形DEBF是平行四边形;证明:
∵四边形ABCD是平行四边形, ∴AO=CO,BO=DO, ∴EO=FO, ∵AE=CF结论还成立1.(中考)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于 .
【解析】∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形, ∴AO=
答案:3 2.(中考)如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.
求证:四边形AECF是平行四边形.【证明】∵四边形ABCD是平行四边形,∴OD=OB,
OA=OC,AB∥CD
∴∠DFO=∠BEO,∠FDO=∠EBO
∴△FDO≌△EBO,∴OF=OE
∴四边形AECF是平行四边形.3.已知:如图,A′B′∥BA, B′C′∥CB, C′A′∥AC.
求证:(1)∠ABC=∠B′,
∠CAB=∠A′,∠BCA=∠C′;
(2)△ABC的顶点分别是△B′C′A′各边的中点.【证明】(1)∵A′B′∥BA,C′B′∥BC,
∴四边形ABCB′是平行四边形.
∴∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.23(2)由(1)证得四边形ABCB′是平行四边形.同理,四边形ABA′C是平行四边形.
∴AB=B′C, AB=A′C(平行四边形的对边相等).
∴B′C=A′C.
同理B′A=C′A, A′B=C′B.
∴△ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点. 4、□ ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?GEFDOHCBAGEFDOHCBA解:四边形EFGH是平行四边形
理由是:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵点E,F,G,H分别是OA,OB,OC,OD的中点
∴OE=1/2OA,OG=1/2OC,OF=1/2OB,OH=1/2OD
∴OE=OG,OF=OH
∴四边形EFGH是平行四边形(1)根据定义:两组对边分别平行的四边
形叫做平行四边形。
(2)两组对边分别相等的四边形是平行
四边形。
(3)两组对角分别相等的四边形是平行四
边形。
(4)两条对角线互相平分的四边形是平
行四边形。ABCD再见28
2. 探索两种组成平行四边形的方法,由此发现平行四边形的判定。
平行四边形的对边平行且相等 平行四边形的对角线互相平分平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD4 平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形的性质:对边相等,对角相等,对角线互相平分.?判定性质定义5判定性质定义 问题 如何寻找平行四边形的判定方法? 当我们对前进的方向感到迷茫时,不妨回过头来看看走过的路!6直角三角
形的性质 直角三角
形的判定 勾股定理 勾股定理
的逆定理 在过去的学习中,类似的情况还有吗?请举例说明.这些经验可以给我们怎样的启示?7两组对边分别相等的
四边形是平行四边形 两组对角分别相等的
四边形是平行四边形 对角线互相平分的四
边形是平行四边形 思考:这些猜想正确吗? 活动1 将两长两短的四根细木条用小钉 钉在一起,让相等的木条作为对边,做一个四边形。它是平行四边形吗?
命题1
两组对边分别相等的四边形是平行四边形9 证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形. 两组对边分别相等的四边形是平行四边形. 判定定理1 猜想1 10 证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 两组对角分别相等的四边形是平行四边形. 判定定理2 猜想2 活动2 将两根细木条的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成的四边形是平行四边形吗?命题2 对角线互相平分的四边形是平行四边形12 如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形. 对角线互相平分的四边形是平行四边形. 判定定理3 猜想3 证明:∵ OA=OC,OB=OD,
∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.归纳两组对边分别平行的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;AD∥BC AB∥DCAD=BC AB=DC∠BAD=∠BCD ∠ABC=∠ADC四边形ABCD是平行四边形如图,用符号表示如下:平行四边形有哪些判定方法?对角线互相平分的四边形是平行四边形。OA=OC OB=OD两组对边分别相等的四边形是平行四边形;四边形ABCD是平行四边形四边形ABCD是平行四边形四边形ABCD是平行四边形判断下列四边形是否是平行四边形?并说明理由.BADC110°110°⑴⑶ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵70°15证明:
∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF. 例1 如图,AB=DC=EF,AD=BC,DE=CF.
求证:AB∥EF.图中还有哪些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:17 例2 如图,平行四边形ABCD中,E,F分别是对角线AC 上的两点,并且 AE=CF.
求证:四边形BFDE是平行四边形.O ∴四边形DEBF是平行四边形;证明:
∵四边形ABCD是平行四边形, ∴AO=CO,BO=DO, ∴EO=FO, ∵AE=CF你还有其它的证法吗?18O 在上题中,若点E,F 分别在AC 两侧的延长线上,如图,其他条件不变,结论还成立吗?请证明你的结论. ∴四边形DEBF是平行四边形;证明:
∵四边形ABCD是平行四边形, ∴AO=CO,BO=DO, ∴EO=FO, ∵AE=CF结论还成立1.(中考)如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于 .
【解析】∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形, ∴AO=
答案:3 2.(中考)如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.
求证:四边形AECF是平行四边形.【证明】∵四边形ABCD是平行四边形,∴OD=OB,
OA=OC,AB∥CD
∴∠DFO=∠BEO,∠FDO=∠EBO
∴△FDO≌△EBO,∴OF=OE
∴四边形AECF是平行四边形.3.已知:如图,A′B′∥BA, B′C′∥CB, C′A′∥AC.
求证:(1)∠ABC=∠B′,
∠CAB=∠A′,∠BCA=∠C′;
(2)△ABC的顶点分别是△B′C′A′各边的中点.【证明】(1)∵A′B′∥BA,C′B′∥BC,
∴四边形ABCB′是平行四边形.
∴∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.23(2)由(1)证得四边形ABCB′是平行四边形.同理,四边形ABA′C是平行四边形.
∴AB=B′C, AB=A′C(平行四边形的对边相等).
∴B′C=A′C.
同理B′A=C′A, A′B=C′B.
∴△ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点. 4、□ ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?GEFDOHCBAGEFDOHCBA解:四边形EFGH是平行四边形
理由是:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵点E,F,G,H分别是OA,OB,OC,OD的中点
∴OE=1/2OA,OG=1/2OC,OF=1/2OB,OH=1/2OD
∴OE=OG,OF=OH
∴四边形EFGH是平行四边形(1)根据定义:两组对边分别平行的四边
形叫做平行四边形。
(2)两组对边分别相等的四边形是平行
四边形。
(3)两组对角分别相等的四边形是平行四
边形。
(4)两条对角线互相平分的四边形是平
行四边形。ABCD再见28
