人教版数学八年级下册 18.1.2 平行四边形的判定(共21张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2 平行四边形的判定(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 383.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-06 00:00:00 | ||
图片预览

文档简介
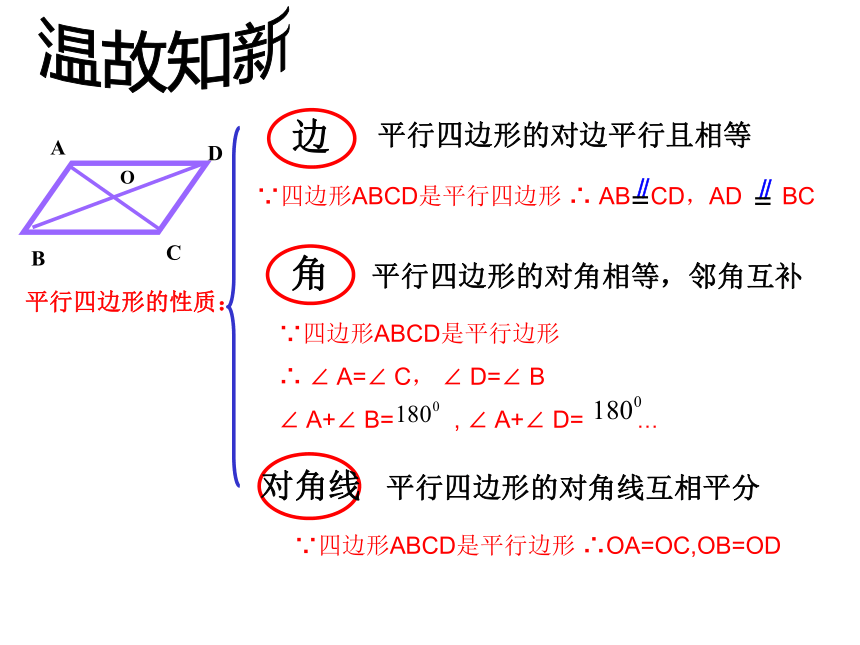
课件21张PPT。平行四边形的判定平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
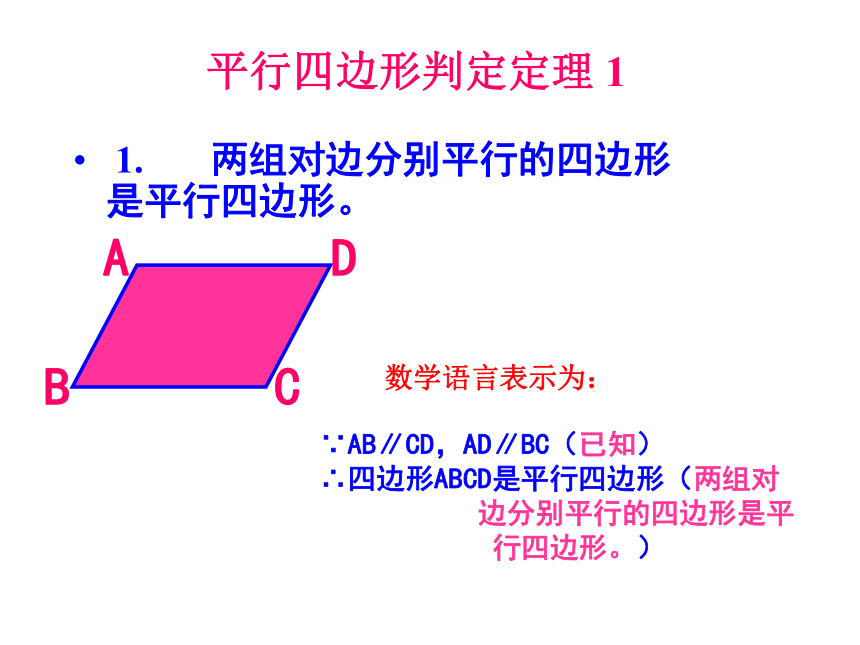
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD平行四边形判定定理 1 1. 两组对边分别平行的四边形是平行四边形。 ∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对
边分别平行的四边形是平
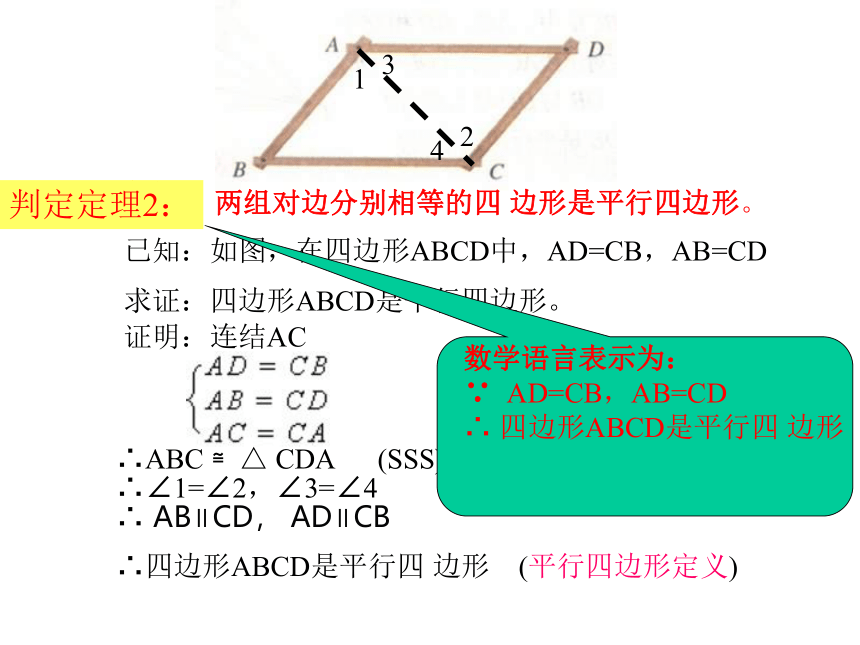
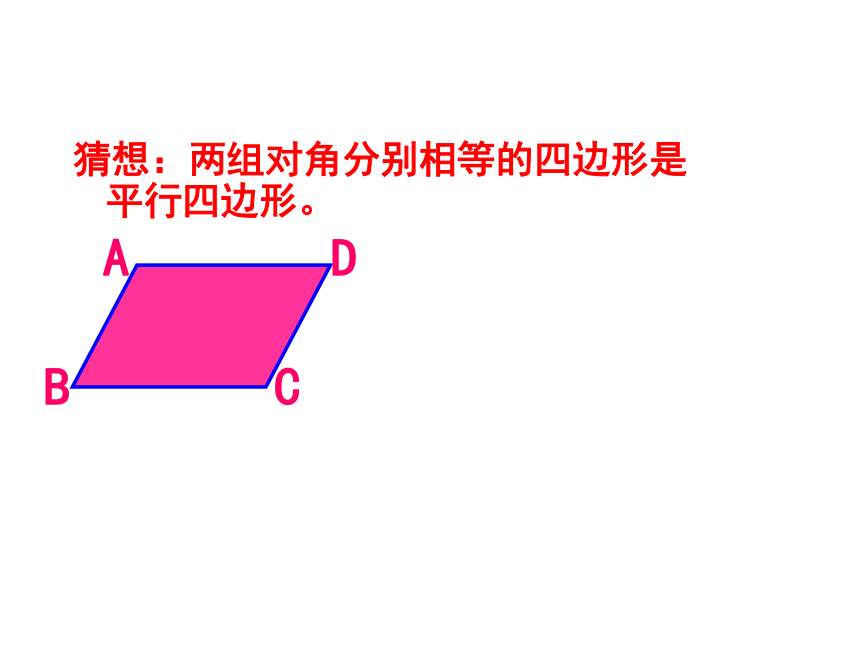
行四边形。) 数学语言表示为:猜想:两组对边分别相等的四 边形是平行四边形。 已知:如图,在四边形ABCD中,AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS) ∴∠1=∠2,∠3=∠41234∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义)判定定理2:猜想:两组对角分别相等的四边形是平行四边形。 BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
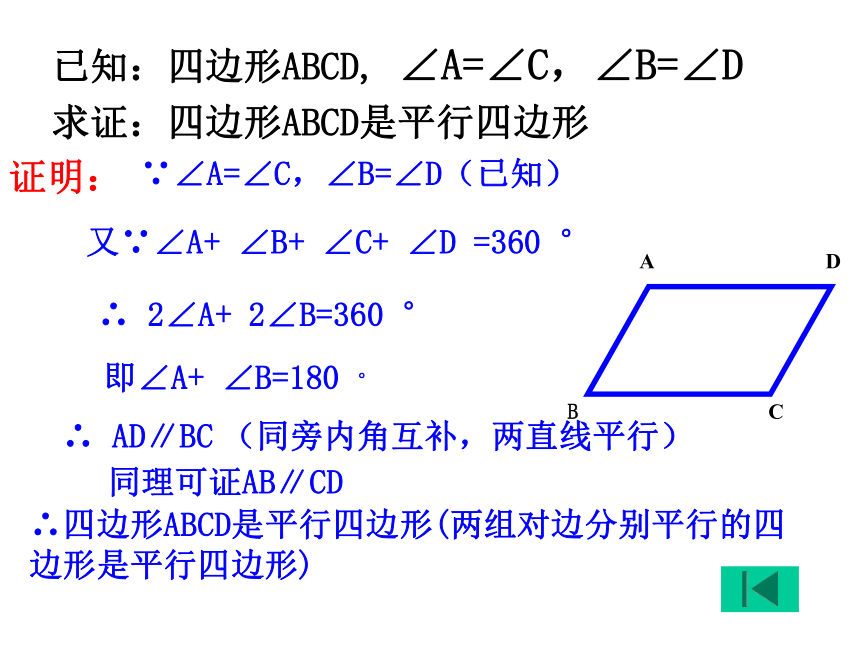
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
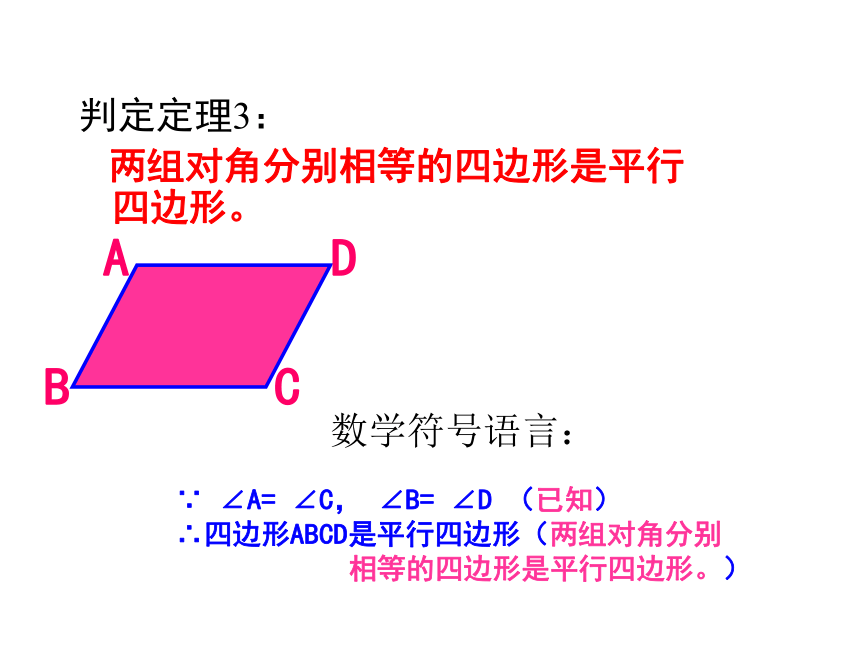
判定定理3:
两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别
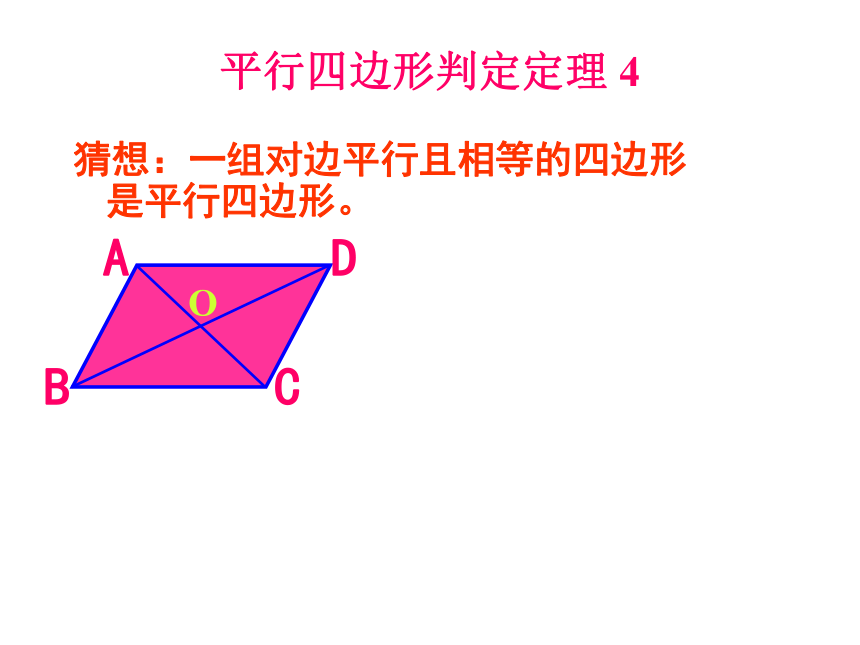
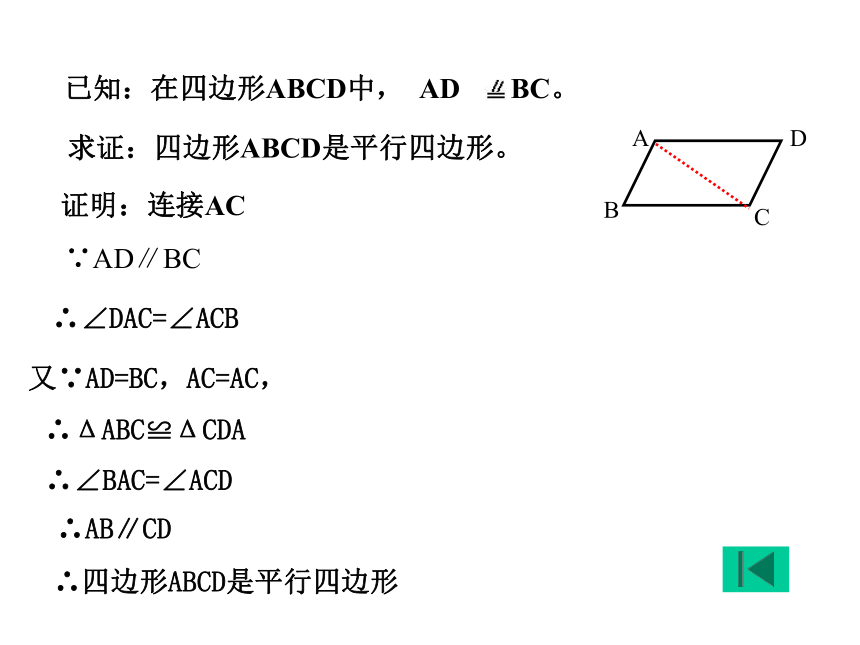
相等的四边形是平行四边形。)数学符号语言:平行四边形判定定理 4猜想:一组对边平行且相等的四边形是平行四边形。 O求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 平行四边形判定定理 4判定定理4:一组对边平行且相等的四边形是平行四边形。 ∵ AD=BC,AD∥BC (已知)
∴四边形ABCD是平行四边形(一组对边平行
且相等的四边形是平行四边形。)O数学语言表示为:猜想:对角线互相平分的四边形是平行四边形。已知:如图,四边形ABCD的对角线AC,BD相交于点O,
并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
平行四边形判定定理 5从边来判定1、两组对边分别平行的四边形是平行四边形(定义) 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法试一试1.判断下列四边形是否是平行四边形?并说明理由.BADC110°110°(1)(3)ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝(2)70°1、在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=___ cm, DO= ____cm时,四边形ABCD为平行四边形.
2、在下列条件中,不能判定四边形是平行四边形的是( )
(A) AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C) AB∥CD,AD=BC练习(两组对边分别平行)(两组对边分别相等)C练习3、 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪 些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:大显身手已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
1.已知:如图,E,F分别是 平行四边形ABCD 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AD∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。能 力 提 升 2.已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123证明:∵AD是ΔABC的角平分线
∴∠1=∠2
∵DE∥AB
∴∠1=∠3
∴∠2=∠3
∴AE=DE
∵BF=AE
∴BF=DE
∵BF∥DE
∴四边形BDEF是平行四边形 (一组对边平行且相等的四边形是平行四边形)
∴EF=BD(平行四边形的对边相等) 3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,交AB于P,BC于Q。
求证:PM=QN。证明:
∵四边形ABCD是平行四边形
∴AB∥CD, AD∥BC
∵MN∥AC
∴四边形AMQC和四边形APNC都是平行四边形
∴AC=MQ , AC=PN (平行四边形的对边相等)
∴MP=PN
∴MP-PQ=PN-PQ
∴PM=QN1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。5、对角线互相平分的四边形是平行四边形。 3、两组对角分别相等的四边形是平行四边形4 、一组对边平行且相等的四边形是平行四边形。谈谈你的收获:作业:教材P47练习 第1、2、3题。
习题18.1 第4、5题。
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD平行四边形判定定理 1 1. 两组对边分别平行的四边形是平行四边形。 ∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对
边分别平行的四边形是平
行四边形。) 数学语言表示为:猜想:两组对边分别相等的四 边形是平行四边形。 已知:如图,在四边形ABCD中,AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS) ∴∠1=∠2,∠3=∠41234∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义)判定定理2:猜想:两组对角分别相等的四边形是平行四边形。 BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
判定定理3:
两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别
相等的四边形是平行四边形。)数学符号语言:平行四边形判定定理 4猜想:一组对边平行且相等的四边形是平行四边形。 O求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 平行四边形判定定理 4判定定理4:一组对边平行且相等的四边形是平行四边形。 ∵ AD=BC,AD∥BC (已知)
∴四边形ABCD是平行四边形(一组对边平行
且相等的四边形是平行四边形。)O数学语言表示为:猜想:对角线互相平分的四边形是平行四边形。已知:如图,四边形ABCD的对角线AC,BD相交于点O,
并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
平行四边形判定定理 5从边来判定1、两组对边分别平行的四边形是平行四边形(定义) 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法试一试1.判断下列四边形是否是平行四边形?并说明理由.BADC110°110°(1)(3)ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝(2)70°1、在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=___ cm, DO= ____cm时,四边形ABCD为平行四边形.
2、在下列条件中,不能判定四边形是平行四边形的是( )
(A) AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C) AB∥CD,AD=BC练习(两组对边分别平行)(两组对边分别相等)C练习3、 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪 些互相平行的线段?解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF AD∥BC AB=DC AD=BC四边形ABCD是平行四边形AB∥DCDC∥EF DC=EF DE=CF四边形CDEF是平行四边形DE∥CFAB∥ DC∥EF理由如下:大显身手已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
1.已知:如图,E,F分别是 平行四边形ABCD 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AD∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。能 力 提 升 2.已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123证明:∵AD是ΔABC的角平分线
∴∠1=∠2
∵DE∥AB
∴∠1=∠3
∴∠2=∠3
∴AE=DE
∵BF=AE
∴BF=DE
∵BF∥DE
∴四边形BDEF是平行四边形 (一组对边平行且相等的四边形是平行四边形)
∴EF=BD(平行四边形的对边相等) 3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,交AB于P,BC于Q。
求证:PM=QN。证明:
∵四边形ABCD是平行四边形
∴AB∥CD, AD∥BC
∵MN∥AC
∴四边形AMQC和四边形APNC都是平行四边形
∴AC=MQ , AC=PN (平行四边形的对边相等)
∴MP=PN
∴MP-PQ=PN-PQ
∴PM=QN1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。5、对角线互相平分的四边形是平行四边形。 3、两组对角分别相等的四边形是平行四边形4 、一组对边平行且相等的四边形是平行四边形。谈谈你的收获:作业:教材P47练习 第1、2、3题。
习题18.1 第4、5题。
