人教版数学八年级下册 18.2.1 矩形的性质 课件(共29张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.2.1 矩形的性质 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-06 23:05:18 | ||
图片预览




文档简介
课件29张PPT。班级----我的家---全靠学习目标
1.掌握矩形的概念、性质定理及推论。
2.能熟练运用矩形的性质进行有关的证明和计算。
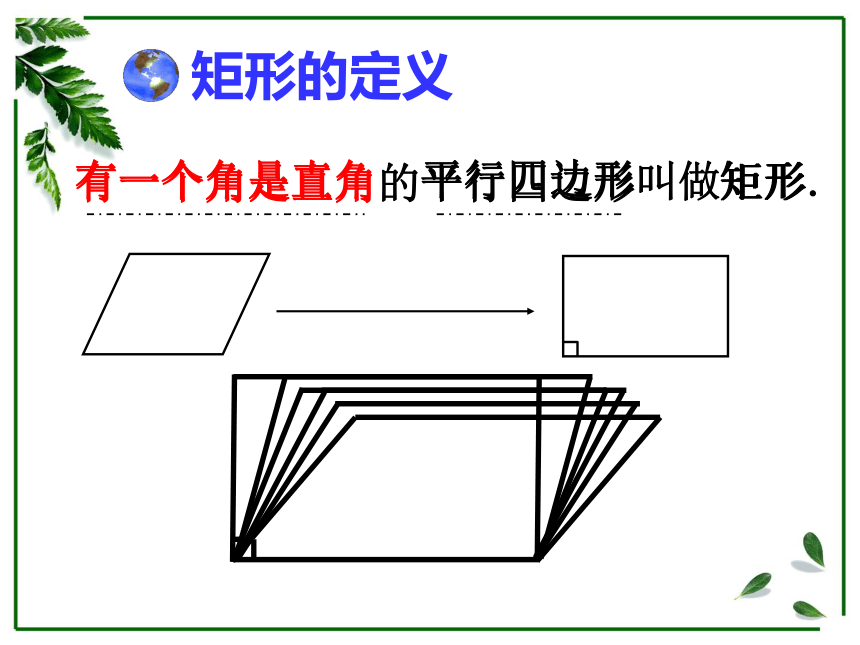
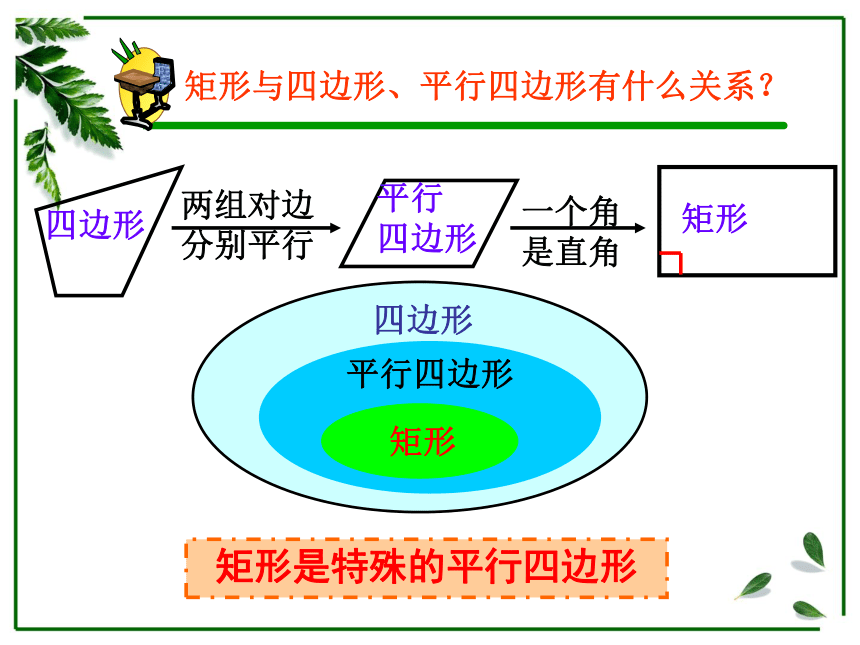
3.掌握直角三角形斜边上的中线的性质。知识回顾:特殊的四边形——平行四边形平行四边形的对边平行且相等平行四边形的对角相等平行四边形的对角线互相平分性质:边角对角线平行四边形 有一个角是直角的平行四边形叫做矩形.有一个角是直角矩形 四边形平行四边形矩形矩形是特殊的平行四边形找一找 你能在生活中找出十种以上矩形吗?具备平行四边形所有的性质对边平行且相等对角相等对角线互相平分矩形的一般性质:探索新知:
矩形除了具有平行四边形的所有性质
外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等. 对角线相等且互相平分四个角都是直角对边平行且相等阶段小结: 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等A.对角相等C.对角线相等 D.对角线互相平分C应用新知已知:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OA=_______ ㎝
OB=_______ ㎝
5105应用新知公平,因为OA=OC=OB=ODOABCD生活链接---投圈游戏◆ 两对全等的等腰三角形.你在矩形中还发现了哪些基本图形?◆ 四个全等的直角三角形.你在矩形中还发现了哪些基本图形?观察图中的Rt△ABC,
在Rt△ABC中,BO是
斜边AC上的中线,BO
与AC有什么关系? 根据矩形的性质,可以得到:思考:直角三角形的性质直角三角形斜边上的中线等于斜边的一半ABCO几何语言:
在Rt△ABC中,O是斜边AC的中点思考:直角三角形的性质例: 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O60°4当堂检测要求:
(1)所有同学6分钟内完成当堂检测A 组题目,组长完成B组题目
(2)题目完成后组长检查组员的题目完成情况,组员记录你在检测中的问题及改错挑战开始1、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分A小试身手2、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
8小试身手如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为16小试身手如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝小试身手已知:如图,BD、CE是△ABC的两条高,M是BC的中点,求证:ME=MD挑战极限命题:矩形的四个角都是直角已知:四边形ABCD是平行四边形, ∠A=90°求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是平行四边形∠A=90°∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90° AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等命题:矩形的对角线相等你还有别的证明方法吗?∵∠ABC=90 °
∴□ABCD是矩形D证明: 延长BO至D,使OD=BO, 连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.∴AC=BD∴BO= BD= AC这
堂
课
你
学
到
了
什
么?回味无穷
1.掌握矩形的概念、性质定理及推论。
2.能熟练运用矩形的性质进行有关的证明和计算。
3.掌握直角三角形斜边上的中线的性质。知识回顾:特殊的四边形——平行四边形平行四边形的对边平行且相等平行四边形的对角相等平行四边形的对角线互相平分性质:边角对角线平行四边形 有一个角是直角的平行四边形叫做矩形.有一个角是直角矩形 四边形平行四边形矩形矩形是特殊的平行四边形找一找 你能在生活中找出十种以上矩形吗?具备平行四边形所有的性质对边平行且相等对角相等对角线互相平分矩形的一般性质:探索新知:
矩形除了具有平行四边形的所有性质
外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等. 对角线相等且互相平分四个角都是直角对边平行且相等阶段小结: 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等A.对角相等C.对角线相等 D.对角线互相平分C应用新知已知:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OA=_______ ㎝
OB=_______ ㎝
5105应用新知公平,因为OA=OC=OB=ODOABCD生活链接---投圈游戏◆ 两对全等的等腰三角形.你在矩形中还发现了哪些基本图形?◆ 四个全等的直角三角形.你在矩形中还发现了哪些基本图形?观察图中的Rt△ABC,
在Rt△ABC中,BO是
斜边AC上的中线,BO
与AC有什么关系? 根据矩形的性质,可以得到:思考:直角三角形的性质直角三角形斜边上的中线等于斜边的一半ABCO几何语言:
在Rt△ABC中,O是斜边AC的中点思考:直角三角形的性质例: 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O60°4当堂检测要求:
(1)所有同学6分钟内完成当堂检测A 组题目,组长完成B组题目
(2)题目完成后组长检查组员的题目完成情况,组员记录你在检测中的问题及改错挑战开始1、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分A小试身手2、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
8小试身手如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为16小试身手如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝小试身手已知:如图,BD、CE是△ABC的两条高,M是BC的中点,求证:ME=MD挑战极限命题:矩形的四个角都是直角已知:四边形ABCD是平行四边形, ∠A=90°求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是平行四边形∠A=90°∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90° AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等命题:矩形的对角线相等你还有别的证明方法吗?∵∠ABC=90 °
∴□ABCD是矩形D证明: 延长BO至D,使OD=BO, 连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.∴AC=BD∴BO= BD= AC这
堂
课
你
学
到
了
什
么?回味无穷
