7.7.动能和动能定理 课件(共36张PPT)
文档属性
| 名称 | 7.7.动能和动能定理 课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 390.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-04-07 13:52:20 | ||
图片预览











文档简介
课件36张PPT。第七节
动能和动能定理一 探究动能的表达式:问题1:什么是动能?物体的动能和什么因素有关? 思考:一架飞机在牵引力作用下(不计空气阻力),在飞机跑道上加速运动,分析:
(1)飞机的动能有没有变化?
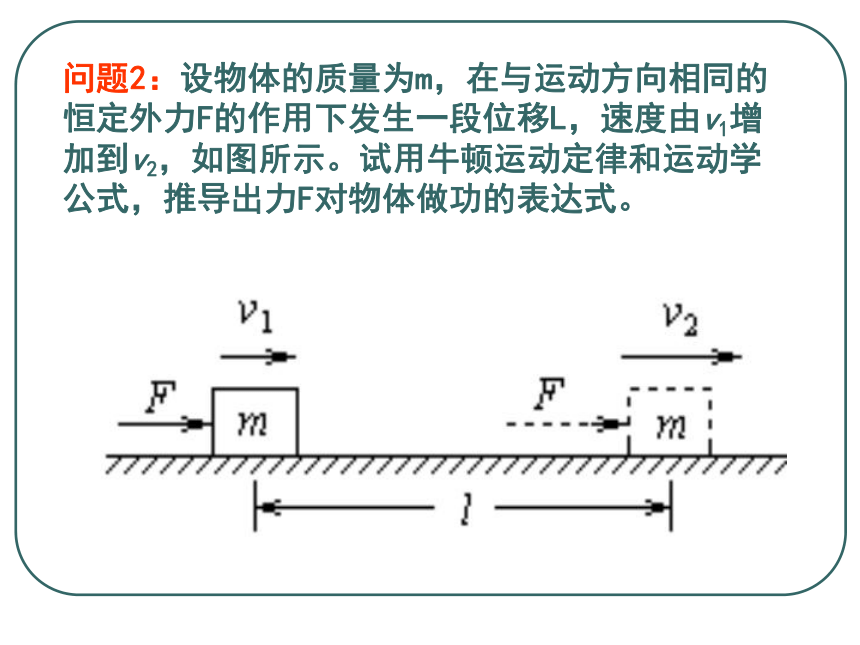
(2)飞机动能变化的原因是什么?问题2:设物体的质量为m,在与运动方向相同的
恒定外力F的作用下发生一段位移L,速度由v1增
加到v2,如图所示。试用牛顿运动定律和运动学
公式,推导出力F对物体做功的表达式。 一 探究动能的表达式:一 探究动能的表达式:1、动能:物体由于运动而具有的能量叫动能.3、物体的动能等于物体的质量与物体速度
的二次方的乘积的一半.4、物理意义:描述运动状态的物理量,
动能是标量,且恒为正值,具有瞬时性5 单位:焦耳( J )例题 我国发射的第一颗人造地球卫星,质量为173
kg,轨道速度为7.2km/s,求它的动能是多少?
解:根据 得,卫星动能:例题:关于对动能的理解,下列说法是正确的
( )A、动能是机械能的一种表现形式,凡是运动的
物体都具有动能B、动能总是非负值C、一定质量的物体,动能变化时,速度一定
变化;但速度变化时,动能不一定变化D、动能不变的物体,一定处于平衡状态A B C问题探究3:1.一质为2kg的物体做自由落体运动,经过A点时的速度为10m/s,到达B点时的速度是20m/s,求:
(1) 经过A、B两点时的动能分别是多少?
(2) 从A到B动能变化了多少?
(3) 从A到B的过程中重力做了多少功?
(4) 从A到B的过程中重力做功与动能的变化关系如何?
在A点时的动能为:在B点时的动能为:(2)从A到B动能的变化量为:问题探究4:
质量为m的物体在水平方向上受到恒定的牵引力F和阻力f作用,经A处时的动能为 ,发生一段位移S后到达位置B时的动能 ,请利用牛顿定律及运动学公式试推导在这过程中,力对物体做功与物体动能的变化关系。∴外力对物体做的总功为:解:f做功为:由① ② ③ 得:动能定理1 内容:合力所做的功等于物体动能的变化.②曲线运动或直线运动③单个物体或几个物体④一个过程或全过程注意点:①“=”是数值上相等,而不是就是②做功引起能的变化对于功与能的关系,下列说法中正确的是( )
A、功就是能,能就是功
B、功可以变成能,能可以变成功
C、做功的过程就是能量转化的过程
D、功是能量的量度
C 例:某同学从高为h 处以速度v0 水平投出一个质量为m 的铅球,求铅球落地时速度大小。
分析与解:铅球在空中运动时只有重力做功,动能增加。设铅球的末速度为v,根据动能定理有 化简得 2 g h= v 2-v02 应用动能定理解题的一般步骤:①确定研究对象,画出草图;
②分析物体的受力情况,分析各力做功的情况;
③确定物体的初、末状态;明确初、末状态的动能
④列式求解;
⑤对结果进行分析讨论。例:一架喷气式飞机,质量m =5×103kg,起飞过程中从静止开始滑跑的路程为s =5.3×102m时,达到起飞的速度 v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02),求飞机受到的牵引力。解法一:飞机受到重力G、支持力N、牵引力F 和阻力f 作用,这四个力做的功分别为WG=0,WN=0,WF=Fs,Wf=-kmgs.据动能定理得: 代入数据得:v0=0m/sv=60m/ss=5.3×102m动能定理与牛顿第二定律的区别 牛顿第二定律是矢量式,反映的是力与加速度的瞬时关系;
动能定理是标量式,反映做功过程中功与始末状态动能增量的关系。 动能定理不涉及物体运动过程中的加速度和时间,因此用它处理问题有时很方便。小结:
一、动能
1、定义:物体由于运动而具有的能量叫做
动能
2、表达式:EK = 1/2·M·V2
二、动能定理
1、内容:合力所做的功等于物体动能的变化
2、表达式:W=1/2·M·V22-1/2·M·V12一人用平均100牛的力把2Kg足球以10m/s踢出,水平飞出100米,求此人对球做功练习1一辆质量m、速度为vo的汽车在关闭发动机后于水平地面滑行了距离L后停了下来。试求汽车受到的阻力。练习2应用动能定理解题步骤: 动能定理的表达式是个标量方程,一般以地面为参考系,凡是与位移相关的质点动力学问题,一般都可以应用动能定理求解。应用动定理解题的一般步聚:
①选择研究对象,进行受力分析;
②分析各力做功的情况;
③确定研究过程(有时有几个过程)的初、末态;
④根据动能定理列方程求解。例1. 质量为m=3kg的物体与水平地面之间的动摩擦因数μ=0.2,在水平恒力F=9N作用下起动,如图所示。当m位移s1=8m时撤去推力F,试问:还能滑多远?(g取10m/s2)
分析:物体m所受重力G、支持力N、推力F、滑动摩擦力f均为恒力,因此物体做匀加速直线运动;撤去F后,物体做匀减速直线运动.因此,可用牛顿定律和匀变速直线运动规律求解.
物体在动力F和阻力f作用下运动时,G和N不做功,F做正功,f做负功,因此,也可以用动能定理求解.
解法一:用牛顿定律和匀变速运动规律,对撤去F推力前、后物体运动的加速度分别为m在匀加速运动阶段的末速度为将上两式相加,得答:撤去动力F后,物体m还能滑4m远 可否对全程运用动能定理?
练习1: 质量为m的物体从以速度v0竖直向上抛出,物体落回地面时,速度大小为3v0/4。(设物体在运动中所受空气阻力大小不变),求:
(1)物体运动过程中所受空气阻力的大小。
(2)物体以初速度2v0竖直向上抛出时,上升的最大高度。如物体与地面碰撞过程中无能量损失,求物体运动的总路程。练习2: 如图所示,斜面的倾角为θ,质量为m的滑块距挡板P为s0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ。滑块所受摩擦力小于滑块沿斜面的下滑力。若滑块每次与挡板相碰均无机械能损失,求滑块经过的路程。 某消防队员从一平台上跳下,下落2m后双脚触地,接着他用双腿弯屈的方法缓冲,使自身重心又下降了0.5m,在着地过程中地面对他双脚的平均作用力估计为自身所受重力的 [ ]
A.2倍 B.5倍
C.8倍 D.10倍
答案:B练习3例2: 一质量为m的小球,用长为L的轻绳悬挂于天花板上,小球在水平力F的作用下,从平衡位置P点缓慢地移到Q点,此时绳子转过了θ角,如图所示,则F做的功为( )
A.mgLcosθ B.mgL(1-cosθ)
C.FLsinθ D.FLθ答案:B例3 一个质量为2kg的物体静止在水平面上,一个水平恒力F推动物体运动了10s钟,然后撤去推力F,物体又滑行了5s才停下来,物体运动的v—t图像如图所示,则推力F做的功和摩擦力在后5s内做的功分别为多少?
答案:2700J例5: 如图所示,在一块水平放置的光滑板面中心开一小孔O,穿过一根细绳,细绳的一端用力F的向下拉,另一端系一小球,并使小球在板面上以半径r做匀速圆周运动。现开始缓慢地增大拉力F,使小球的运动半径逐渐减小,若已知拉力变为8F时,小球的运动半径恰好减为r/2,求在此过程中,绳子的拉力对小球所做的功。答案 :3Fr/2例6: 一个物体以初速度Vo=l0m/s自斜面底端向上滑行,如图所示,到达斜面顶端时恰好静止,随后物体向下滑行返回底端时的速度为5m/s,求斜面的高度是多少?若该斜面的倾角θ=30°,则物体与斜面间的动摩擦因数是多少?(取g=lOm/s2)例7: 如图所示,一个小滑块质量为m,在倾角θ=37°的斜面上从高为h=25cm处由静止开始下滑,滑到斜面底端时与挡板P发生弹性碰撞后又沿斜面上滑,若滑块与斜面之间的动摩擦因数μ=0.25,求滑块在斜面上运动的总路程.
谢 谢!
动能和动能定理一 探究动能的表达式:问题1:什么是动能?物体的动能和什么因素有关? 思考:一架飞机在牵引力作用下(不计空气阻力),在飞机跑道上加速运动,分析:
(1)飞机的动能有没有变化?
(2)飞机动能变化的原因是什么?问题2:设物体的质量为m,在与运动方向相同的
恒定外力F的作用下发生一段位移L,速度由v1增
加到v2,如图所示。试用牛顿运动定律和运动学
公式,推导出力F对物体做功的表达式。 一 探究动能的表达式:一 探究动能的表达式:1、动能:物体由于运动而具有的能量叫动能.3、物体的动能等于物体的质量与物体速度
的二次方的乘积的一半.4、物理意义:描述运动状态的物理量,
动能是标量,且恒为正值,具有瞬时性5 单位:焦耳( J )例题 我国发射的第一颗人造地球卫星,质量为173
kg,轨道速度为7.2km/s,求它的动能是多少?
解:根据 得,卫星动能:例题:关于对动能的理解,下列说法是正确的
( )A、动能是机械能的一种表现形式,凡是运动的
物体都具有动能B、动能总是非负值C、一定质量的物体,动能变化时,速度一定
变化;但速度变化时,动能不一定变化D、动能不变的物体,一定处于平衡状态A B C问题探究3:1.一质为2kg的物体做自由落体运动,经过A点时的速度为10m/s,到达B点时的速度是20m/s,求:
(1) 经过A、B两点时的动能分别是多少?
(2) 从A到B动能变化了多少?
(3) 从A到B的过程中重力做了多少功?
(4) 从A到B的过程中重力做功与动能的变化关系如何?
在A点时的动能为:在B点时的动能为:(2)从A到B动能的变化量为:问题探究4:
质量为m的物体在水平方向上受到恒定的牵引力F和阻力f作用,经A处时的动能为 ,发生一段位移S后到达位置B时的动能 ,请利用牛顿定律及运动学公式试推导在这过程中,力对物体做功与物体动能的变化关系。∴外力对物体做的总功为:解:f做功为:由① ② ③ 得:动能定理1 内容:合力所做的功等于物体动能的变化.②曲线运动或直线运动③单个物体或几个物体④一个过程或全过程注意点:①“=”是数值上相等,而不是就是②做功引起能的变化对于功与能的关系,下列说法中正确的是( )
A、功就是能,能就是功
B、功可以变成能,能可以变成功
C、做功的过程就是能量转化的过程
D、功是能量的量度
C 例:某同学从高为h 处以速度v0 水平投出一个质量为m 的铅球,求铅球落地时速度大小。
分析与解:铅球在空中运动时只有重力做功,动能增加。设铅球的末速度为v,根据动能定理有 化简得 2 g h= v 2-v02 应用动能定理解题的一般步骤:①确定研究对象,画出草图;
②分析物体的受力情况,分析各力做功的情况;
③确定物体的初、末状态;明确初、末状态的动能
④列式求解;
⑤对结果进行分析讨论。例:一架喷气式飞机,质量m =5×103kg,起飞过程中从静止开始滑跑的路程为s =5.3×102m时,达到起飞的速度 v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02),求飞机受到的牵引力。解法一:飞机受到重力G、支持力N、牵引力F 和阻力f 作用,这四个力做的功分别为WG=0,WN=0,WF=Fs,Wf=-kmgs.据动能定理得: 代入数据得:v0=0m/sv=60m/ss=5.3×102m动能定理与牛顿第二定律的区别 牛顿第二定律是矢量式,反映的是力与加速度的瞬时关系;
动能定理是标量式,反映做功过程中功与始末状态动能增量的关系。 动能定理不涉及物体运动过程中的加速度和时间,因此用它处理问题有时很方便。小结:
一、动能
1、定义:物体由于运动而具有的能量叫做
动能
2、表达式:EK = 1/2·M·V2
二、动能定理
1、内容:合力所做的功等于物体动能的变化
2、表达式:W=1/2·M·V22-1/2·M·V12一人用平均100牛的力把2Kg足球以10m/s踢出,水平飞出100米,求此人对球做功练习1一辆质量m、速度为vo的汽车在关闭发动机后于水平地面滑行了距离L后停了下来。试求汽车受到的阻力。练习2应用动能定理解题步骤: 动能定理的表达式是个标量方程,一般以地面为参考系,凡是与位移相关的质点动力学问题,一般都可以应用动能定理求解。应用动定理解题的一般步聚:
①选择研究对象,进行受力分析;
②分析各力做功的情况;
③确定研究过程(有时有几个过程)的初、末态;
④根据动能定理列方程求解。例1. 质量为m=3kg的物体与水平地面之间的动摩擦因数μ=0.2,在水平恒力F=9N作用下起动,如图所示。当m位移s1=8m时撤去推力F,试问:还能滑多远?(g取10m/s2)
分析:物体m所受重力G、支持力N、推力F、滑动摩擦力f均为恒力,因此物体做匀加速直线运动;撤去F后,物体做匀减速直线运动.因此,可用牛顿定律和匀变速直线运动规律求解.
物体在动力F和阻力f作用下运动时,G和N不做功,F做正功,f做负功,因此,也可以用动能定理求解.
解法一:用牛顿定律和匀变速运动规律,对撤去F推力前、后物体运动的加速度分别为m在匀加速运动阶段的末速度为将上两式相加,得答:撤去动力F后,物体m还能滑4m远 可否对全程运用动能定理?
练习1: 质量为m的物体从以速度v0竖直向上抛出,物体落回地面时,速度大小为3v0/4。(设物体在运动中所受空气阻力大小不变),求:
(1)物体运动过程中所受空气阻力的大小。
(2)物体以初速度2v0竖直向上抛出时,上升的最大高度。如物体与地面碰撞过程中无能量损失,求物体运动的总路程。练习2: 如图所示,斜面的倾角为θ,质量为m的滑块距挡板P为s0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ。滑块所受摩擦力小于滑块沿斜面的下滑力。若滑块每次与挡板相碰均无机械能损失,求滑块经过的路程。 某消防队员从一平台上跳下,下落2m后双脚触地,接着他用双腿弯屈的方法缓冲,使自身重心又下降了0.5m,在着地过程中地面对他双脚的平均作用力估计为自身所受重力的 [ ]
A.2倍 B.5倍
C.8倍 D.10倍
答案:B练习3例2: 一质量为m的小球,用长为L的轻绳悬挂于天花板上,小球在水平力F的作用下,从平衡位置P点缓慢地移到Q点,此时绳子转过了θ角,如图所示,则F做的功为( )
A.mgLcosθ B.mgL(1-cosθ)
C.FLsinθ D.FLθ答案:B例3 一个质量为2kg的物体静止在水平面上,一个水平恒力F推动物体运动了10s钟,然后撤去推力F,物体又滑行了5s才停下来,物体运动的v—t图像如图所示,则推力F做的功和摩擦力在后5s内做的功分别为多少?
答案:2700J例5: 如图所示,在一块水平放置的光滑板面中心开一小孔O,穿过一根细绳,细绳的一端用力F的向下拉,另一端系一小球,并使小球在板面上以半径r做匀速圆周运动。现开始缓慢地增大拉力F,使小球的运动半径逐渐减小,若已知拉力变为8F时,小球的运动半径恰好减为r/2,求在此过程中,绳子的拉力对小球所做的功。答案 :3Fr/2例6: 一个物体以初速度Vo=l0m/s自斜面底端向上滑行,如图所示,到达斜面顶端时恰好静止,随后物体向下滑行返回底端时的速度为5m/s,求斜面的高度是多少?若该斜面的倾角θ=30°,则物体与斜面间的动摩擦因数是多少?(取g=lOm/s2)例7: 如图所示,一个小滑块质量为m,在倾角θ=37°的斜面上从高为h=25cm处由静止开始下滑,滑到斜面底端时与挡板P发生弹性碰撞后又沿斜面上滑,若滑块与斜面之间的动摩擦因数μ=0.25,求滑块在斜面上运动的总路程.
谢 谢!
