人教版数学七年级下册7.1.2平面直角坐标系作图 课件(共28张PPT)
文档属性
| 名称 | 人教版数学七年级下册7.1.2平面直角坐标系作图 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-07 22:16:03 | ||
图片预览




文档简介
课件28张PPT。7.1.2平面直角坐标系(2)学习目标 1、会根据实际情况建立适当的坐标系;
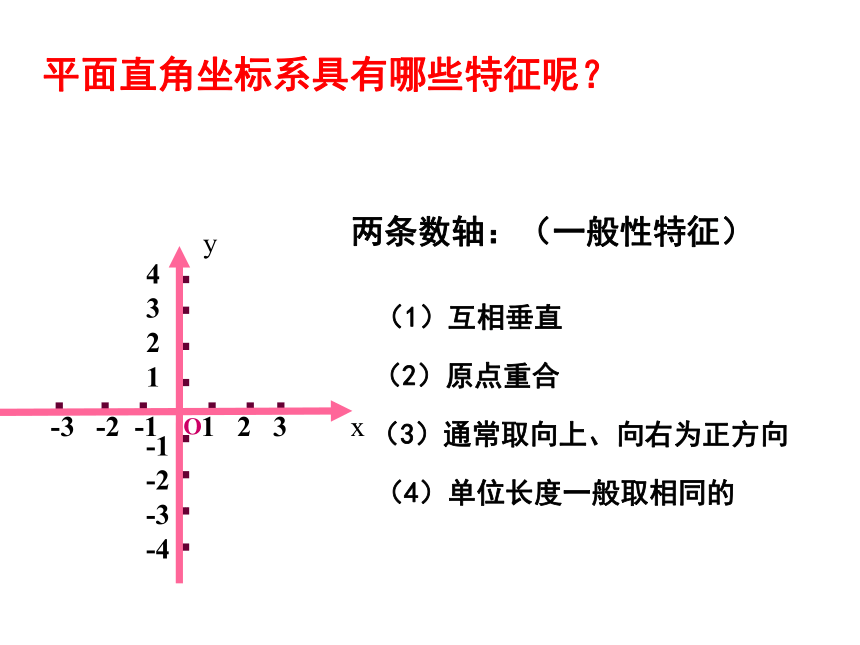
2、通过点的位置关系探索坐标之间的关系及根据坐标之间的关系探索点的位置关系.两条数轴:(一般性特征) (1)互相垂直(2)原点重合 (3)通常取向上、向右为正方向(4)单位长度一般取相同的平面直角坐标系具有哪些特征呢?Oxy -3 -2 -1 1 2 3 4
3
2
1
-1
-2
-3
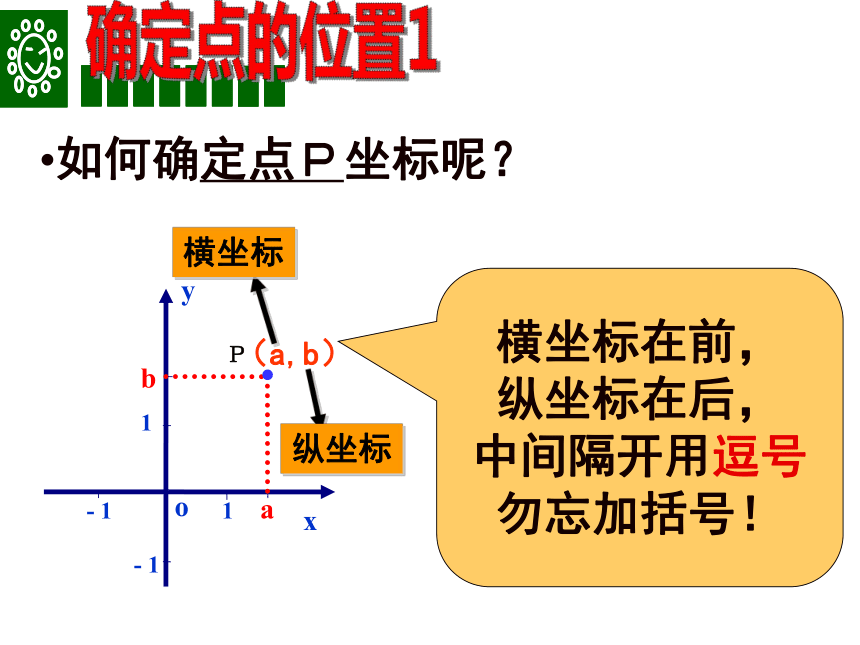
-4xyo-11-11ab P如何确定点P坐标呢?(a,b)横坐标在前,
纵坐标在后,
中间隔开用逗号
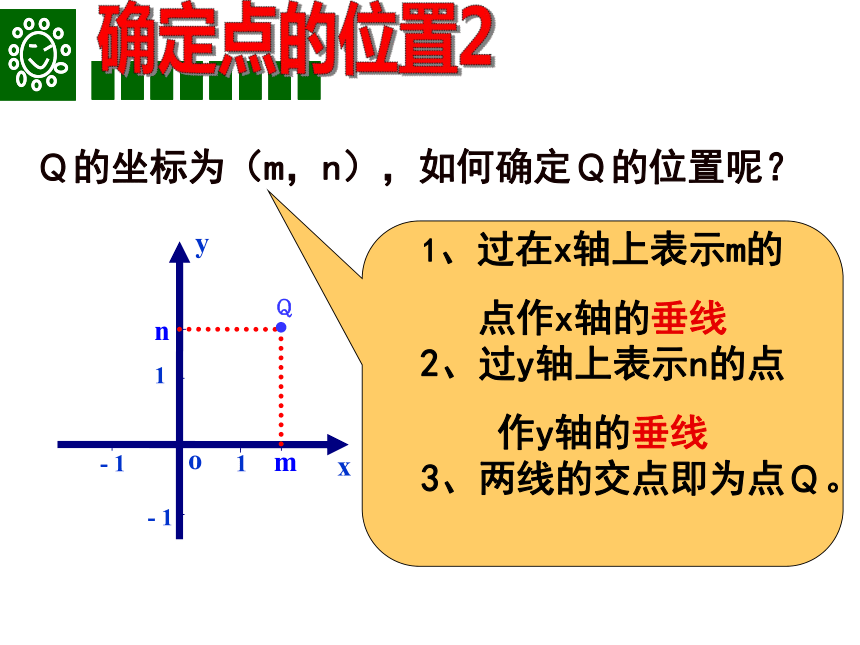
勿忘加括号!横坐标纵坐标Q的坐标为(m,n),如何确定Q的位置呢?yo-11-11mn Qx1、过在x轴上表示m的
点作x轴的垂线 2、过y轴上表示n的点
作y轴的垂线 3、两线的交点即为点Q。
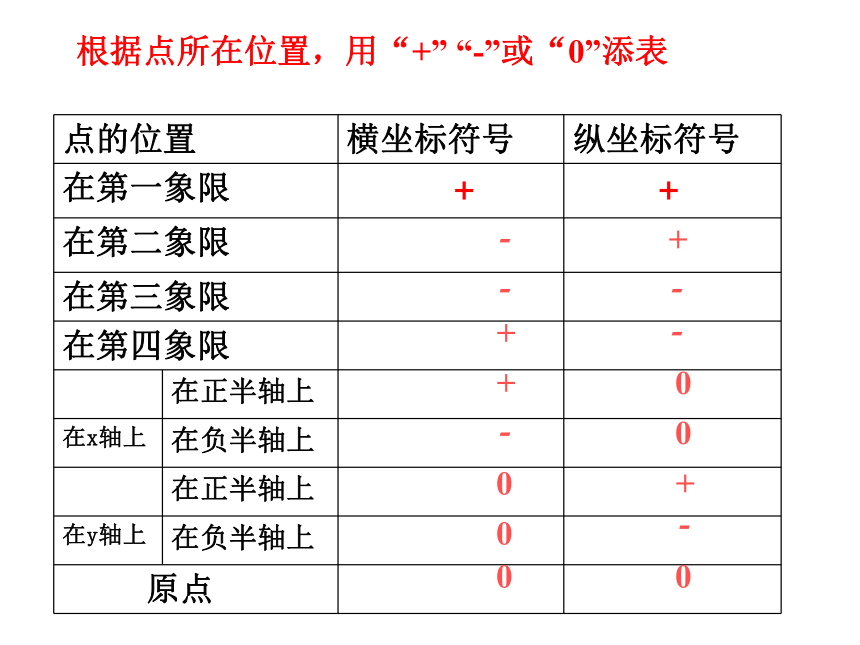
根据点所在位置,用“+” “-”或“0”添表----+++00--00+00结论纵坐标相同的点的连线平行于x轴横坐标相同的点的连线平行于y轴坐标轴的点至少有一个是0
巩固练习:1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
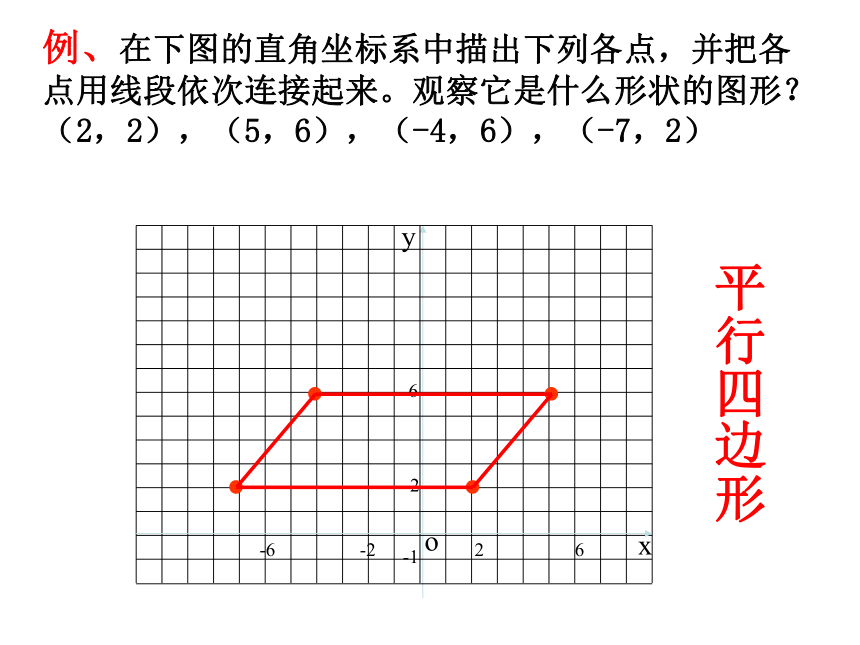
若点(a+1,-5)在y轴上,则a=______. 四三y-1例、在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来。观察它是什么形状的图形?(2,2),(5,6),(-4,6),(-7,2)平行四边形-1oyx-2-6262练一练在平面直角坐标系中描出下列各点:
A(-3,-1),B(-3,2),C(0,2),D(3,2),E(3,-1),F(0,-1)
并用线段顺次连接各点,看看你画出的图形是什么形状?长方形●●●
●●●5 341-3-231-5-3-4FABCDE·-2-3o-11 在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.①(0 , 6), (-4, 3), (4 , 3) ②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)······观察所得的图形,你觉得它象什么?-4-14A(-4,3)B(4,3)C(-2,3)D(2,3)E(-2,-3)F(2,-3)(0 , 6)·归纳:点到两坐标轴的距离
点P(x,y)
到x轴的距离为∣y∣,
到y轴的距离为∣x∣
·-2-3o-11······-4-14(-4,3)(4,3)(-2,3)(2,3)(-2,-3)(2,-3)· 在如图建立的直角坐
标系中读出下列各点.你能发现什么?BCDEFG想一想分别写出图中点A、B、C、D的坐标。观察图形,并回答问题(3,2)(3,-2)-2-14321-3-4-4y123-3-1-2(-3,2)(-3,-2)0点A与点B的位置有什么特点?
点A与点B的坐标有什么关系?点A与点C的位置有什么特点?
点A与点C的坐标有什么关系?
点B与点C的位置有什么特点?
点B与点C的坐标有什么关系?A BCD(-a,b)(a,b)(a,-b)(-a,-b)归纳:1、平面直角坐标系中的点p(x,y) 到x轴的距离是|y| ;
到y轴的距离是 |x|;
2、平面直角坐标系中的点p(x,y)关于x轴的对称点是(x,-y);
关于y轴的对称点是(-x,y);
关于原点的对称点是(-x,-y)。归纳:点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.平行于坐标轴的直线上的点:
⑤.对称于坐标轴的两点:
⑥.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-) 1、点(1,-3)关于X轴的对称点的坐标为______关于Y轴的对称点的坐标为_________,关于原点对称的点的坐标为 _________。2、点(-1,3)关于X轴的对称点的坐标为________,关于Y轴对称点的坐标为______,关于原点的对称点的坐标为____________。(1,3)(-1,-3)(-1,3)(-1,-3)(1,3)(1,-3)巩固练习:4.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是________。3.点 M(- 8,12)到 x轴的距离是_________,到 y轴的距离是________.128(-1.5,-2) 一、判断:
1、对于坐标平面内的任一点,都有唯一
一对有序实数与它对应.( )
2、在直角坐标系内,原点的坐标是0.( )
3、如果点A(a ,-b)在第二象限,那么点B(-a,b)在第四象限.( )√√×练习: 1、在y轴上的点的横坐标是( ),在x轴上的点的纵坐标是( ). 2、点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( ). 3、点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( ). 00(2, 3)( 2,1)4、点 M(- 8,12)到 x轴的距离是( ),到 y轴的距离是( ) . 5、点(4,3)与点(4,- 3)的关系是( ) . (A)关于原点对称 (B)关于 x轴对称 (C)关于 y轴对称 (D)不能构成对称关系128B练习
1、若点P(m,n)在第二象限,则点Q(-m,-n)在第( )象限
2、如果点A(a2+1,-1-b2),那么点A在第几象限.
3、点M(3,-4)关于x轴的对称点M′的坐标是( )
A、(3,4) B、 (-3,-4)
C、 (-3,4) D 、(-4,3)
细心选一选,你准对﹗1.下列点中位于第四象限的是( )
A.(2,-3)B.(-2,-3) C.(2,3)D.(-2,3)
2.如xy>0,且x+y<0,那么P(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如点P(a,2)在第二象限,那么点Q(-3,a)
在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.M(-1,0)、N(0,-1)、P(-2,-1)、Q(5,0)、R(0,-5)、S(-3,2),其中在x轴上 的点的个数是( )
A.1 B.2 C.3 D.4
CCBA一、已知P点坐标为(a-1,a-5)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③若a=-3 ,则P在第 象限内;
④若a=3,则点P在第 象限内.二、若点P(x,y)在第四象限,|x|=2, |y|=3,则P点的坐标为 .5(2,-3)1347.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对8.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限Ba<0b>1B归纳:点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.平行于坐标轴的直线上的点:
⑤.对称于坐标轴的两点:
⑥.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-)
特殊位置的点的坐标特点:
⑴ x轴上的点,纵坐标为0。 y轴上的点,横坐标为0。
⑵ 第一、三象限夹角平分线上的点,纵横坐标相等。
第二、四象限夹角平分线上的点,纵横坐标互为相反数。
⑶与x轴平行(或与y轴垂直)的直线上的点纵坐标都相同。
与y轴平行(或与x轴垂直)的直线上的点横坐标都相同。
⑷关于x轴对称的点横坐标相同、纵坐标互为相反数。
关于y轴对称的点纵坐标相同、横坐标互为相反数。
关于原点对称的点纵横坐标都互为相反数。
⑸平面直角坐标系中有一点P(a , b),点P到x轴的距离是这个点的
纵坐标的绝对值;点P到y轴的距离是这个点的横坐标的绝对值;
注意:上述所有规律,正着说对,反着说也对。
2、通过点的位置关系探索坐标之间的关系及根据坐标之间的关系探索点的位置关系.两条数轴:(一般性特征) (1)互相垂直(2)原点重合 (3)通常取向上、向右为正方向(4)单位长度一般取相同的平面直角坐标系具有哪些特征呢?Oxy -3 -2 -1 1 2 3 4
3
2
1
-1
-2
-3
-4xyo-11-11ab P如何确定点P坐标呢?(a,b)横坐标在前,
纵坐标在后,
中间隔开用逗号
勿忘加括号!横坐标纵坐标Q的坐标为(m,n),如何确定Q的位置呢?yo-11-11mn Qx1、过在x轴上表示m的
点作x轴的垂线 2、过y轴上表示n的点
作y轴的垂线 3、两线的交点即为点Q。
根据点所在位置,用“+” “-”或“0”添表----+++00--00+00结论纵坐标相同的点的连线平行于x轴横坐标相同的点的连线平行于y轴坐标轴的点至少有一个是0
巩固练习:1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______. 四三y-1例、在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来。观察它是什么形状的图形?(2,2),(5,6),(-4,6),(-7,2)平行四边形-1oyx-2-6262练一练在平面直角坐标系中描出下列各点:
A(-3,-1),B(-3,2),C(0,2),D(3,2),E(3,-1),F(0,-1)
并用线段顺次连接各点,看看你画出的图形是什么形状?长方形●●●
●●●5 341-3-231-5-3-4FABCDE·-2-3o-11 在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.①(0 , 6), (-4, 3), (4 , 3) ②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)······观察所得的图形,你觉得它象什么?-4-14A(-4,3)B(4,3)C(-2,3)D(2,3)E(-2,-3)F(2,-3)(0 , 6)·归纳:点到两坐标轴的距离
点P(x,y)
到x轴的距离为∣y∣,
到y轴的距离为∣x∣
·-2-3o-11······-4-14(-4,3)(4,3)(-2,3)(2,3)(-2,-3)(2,-3)· 在如图建立的直角坐
标系中读出下列各点.你能发现什么?BCDEFG想一想分别写出图中点A、B、C、D的坐标。观察图形,并回答问题(3,2)(3,-2)-2-14321-3-4-4y123-3-1-2(-3,2)(-3,-2)0点A与点B的位置有什么特点?
点A与点B的坐标有什么关系?点A与点C的位置有什么特点?
点A与点C的坐标有什么关系?
点B与点C的位置有什么特点?
点B与点C的坐标有什么关系?A BCD(-a,b)(a,b)(a,-b)(-a,-b)归纳:1、平面直角坐标系中的点p(x,y) 到x轴的距离是|y| ;
到y轴的距离是 |x|;
2、平面直角坐标系中的点p(x,y)关于x轴的对称点是(x,-y);
关于y轴的对称点是(-x,y);
关于原点的对称点是(-x,-y)。归纳:点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.平行于坐标轴的直线上的点:
⑤.对称于坐标轴的两点:
⑥.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-) 1、点(1,-3)关于X轴的对称点的坐标为______关于Y轴的对称点的坐标为_________,关于原点对称的点的坐标为 _________。2、点(-1,3)关于X轴的对称点的坐标为________,关于Y轴对称点的坐标为______,关于原点的对称点的坐标为____________。(1,3)(-1,-3)(-1,3)(-1,-3)(1,3)(1,-3)巩固练习:4.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是________。3.点 M(- 8,12)到 x轴的距离是_________,到 y轴的距离是________.128(-1.5,-2) 一、判断:
1、对于坐标平面内的任一点,都有唯一
一对有序实数与它对应.( )
2、在直角坐标系内,原点的坐标是0.( )
3、如果点A(a ,-b)在第二象限,那么点B(-a,b)在第四象限.( )√√×练习: 1、在y轴上的点的横坐标是( ),在x轴上的点的纵坐标是( ). 2、点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( ). 3、点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( ). 00(2, 3)( 2,1)4、点 M(- 8,12)到 x轴的距离是( ),到 y轴的距离是( ) . 5、点(4,3)与点(4,- 3)的关系是( ) . (A)关于原点对称 (B)关于 x轴对称 (C)关于 y轴对称 (D)不能构成对称关系128B练习
1、若点P(m,n)在第二象限,则点Q(-m,-n)在第( )象限
2、如果点A(a2+1,-1-b2),那么点A在第几象限.
3、点M(3,-4)关于x轴的对称点M′的坐标是( )
A、(3,4) B、 (-3,-4)
C、 (-3,4) D 、(-4,3)
细心选一选,你准对﹗1.下列点中位于第四象限的是( )
A.(2,-3)B.(-2,-3) C.(2,3)D.(-2,3)
2.如xy>0,且x+y<0,那么P(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如点P(a,2)在第二象限,那么点Q(-3,a)
在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.M(-1,0)、N(0,-1)、P(-2,-1)、Q(5,0)、R(0,-5)、S(-3,2),其中在x轴上 的点的个数是( )
A.1 B.2 C.3 D.4
CCBA一、已知P点坐标为(a-1,a-5)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③若a=-3 ,则P在第 象限内;
④若a=3,则点P在第 象限内.二、若点P(x,y)在第四象限,|x|=2, |y|=3,则P点的坐标为 .5(2,-3)1347.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对8.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限Ba<0b>1B归纳:点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.平行于坐标轴的直线上的点:
⑤.对称于坐标轴的两点:
⑥.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-)
特殊位置的点的坐标特点:
⑴ x轴上的点,纵坐标为0。 y轴上的点,横坐标为0。
⑵ 第一、三象限夹角平分线上的点,纵横坐标相等。
第二、四象限夹角平分线上的点,纵横坐标互为相反数。
⑶与x轴平行(或与y轴垂直)的直线上的点纵坐标都相同。
与y轴平行(或与x轴垂直)的直线上的点横坐标都相同。
⑷关于x轴对称的点横坐标相同、纵坐标互为相反数。
关于y轴对称的点纵坐标相同、横坐标互为相反数。
关于原点对称的点纵横坐标都互为相反数。
⑸平面直角坐标系中有一点P(a , b),点P到x轴的距离是这个点的
纵坐标的绝对值;点P到y轴的距离是这个点的横坐标的绝对值;
注意:上述所有规律,正着说对,反着说也对。
