北师大版八年级数学下册第三章第一节 图形的平移课件(31张)
文档属性
| 名称 | 北师大版八年级数学下册第三章第一节 图形的平移课件(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-22 12:14:04 | ||
图片预览








文档简介
第三章 图形的平移与旋转
喔,神7上天啦!
探索平移的奥秘
走进生活中的平移世界
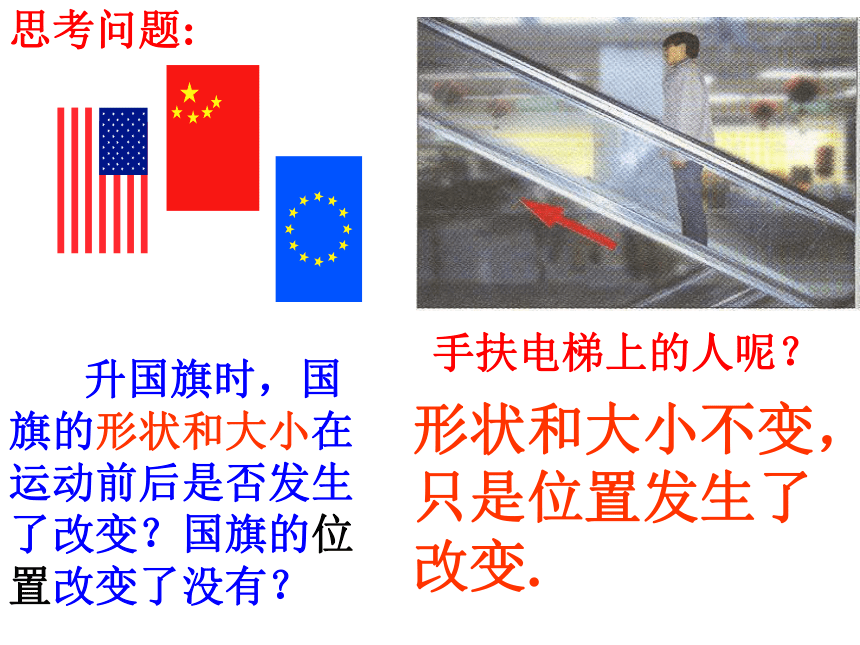
升国旗
上升的水桶
小狗拉着盒子在平整的地面上跑.
天上飞着的飞机
在公路上跑着的汽车
2
1
3
4
5
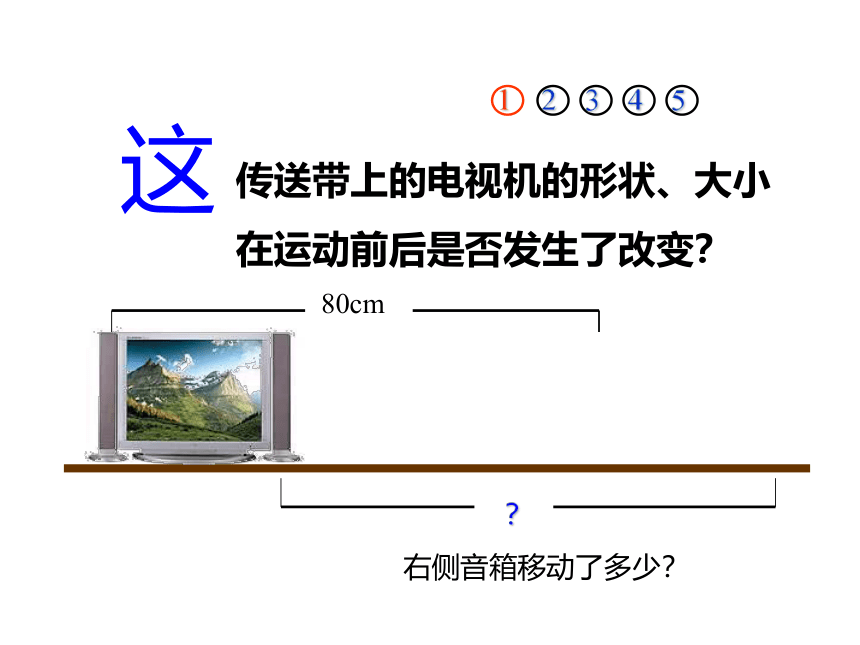
传送带上的电视机的形状、大小在运动前后是否发生了改变?
右侧音箱移动了多少?
这
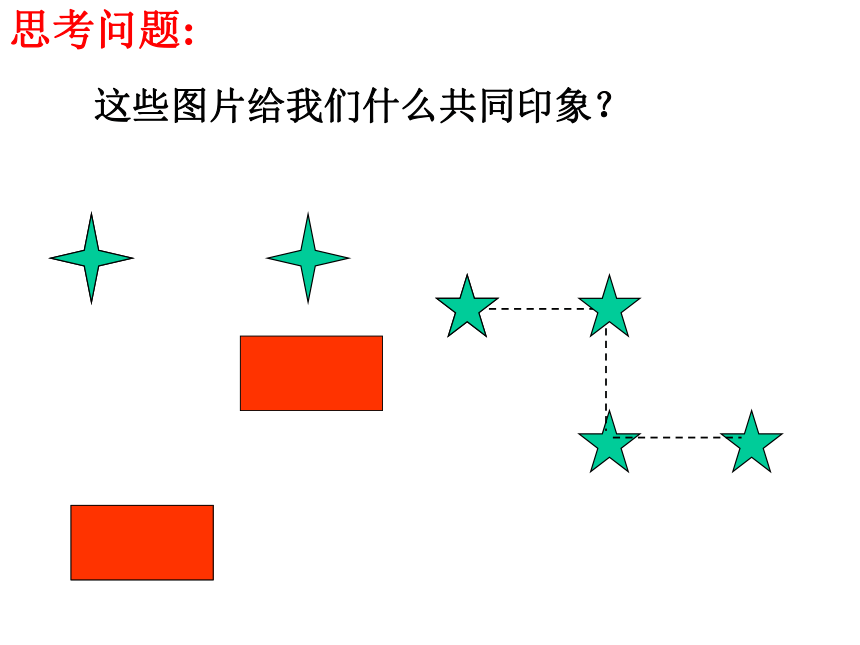
这些图片给我们什么共同印象?
思考问题:
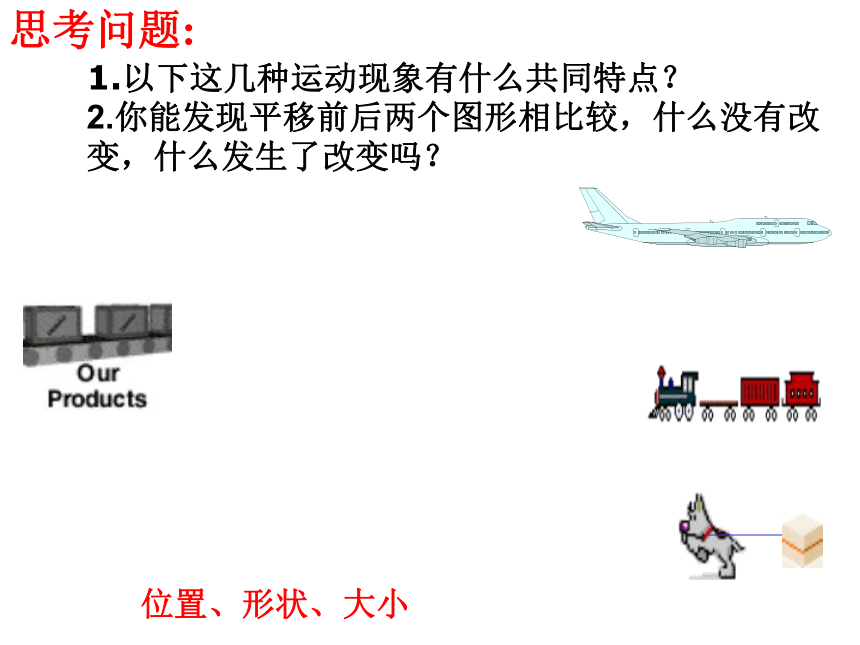
1.以下这几种运动现象有什么共同特点?
2.你能发现平移前后两个图形相比较,什么没有改
变,什么发生了改变吗?
位置、形状、大小
思考问题:
思考问题:
形状和大小不变,只是位置发生了改变.
1、传送带上的电视机的形状大小在运送过程中是否发生了变化?电梯上的人呢?
2、在传送带上,如果电视机的某一按键向前移动了80cm,那么电视机的其它部位(如屏幕左上角的图标)向什么方向移动?移动了多少距离?电梯上的人呢?
3、如果把移动前后的同一台电视机的屏幕分别记做四边形ABCD和四边形EFGH,那么四边形ABCD和四边形EFGH的形状、大小是否相同?
在平面内,
这样的图形运动称为 。
将一个图形沿某个方向移动了
一定的距离 ,
平移
平移两要素:
特征:
平移不改变图形的形状和大小。
1.平移方向
2.平移距离
注:
平移前后的两个图形是全等图形
平移定义:
A
B
C
D
E
F
G
H
在图中,点A,B,C,D分别平移到了点E,F,G,H. A与E,B与F,C与G,D与H分别是一一对应的点;AB与EF是一组对应线段;∠BAD与∠FEH是一对对应角。
在图中,四边形ABCD各顶点分别平移到什么位置? 图中有哪些对应线段和对应角?
A
B
C
D
E
F
X
Y
点A的对应点是点____;点B的对应点是点____;点C的对应点是点____.
线段AB的对应线段是_____;线段BC的对应线段是_____;线段AC的对应线段是_____.
∠A的对应角是_____;
∠ B的对应角是_____
∠ C的对应角是_____.
如图,?ABC经过平移得到?DEF,点A,B,C, 分别平移到了点D.E,F,
E
D
F
DE
EF
DF
∠D
∠E
∠F
2、在图中,线段AE,BF,CG,DH有怎样的关系?
答:线段AE,BF,CG,DH是彼此相等的,平行的。
3、图中每对对应线段之间有怎样的关系?
1、图中有哪些相等的线段、相等的角?
答:相等的线段:AD与EH,BC与FG,AB与EF,DC与HG。 相等的角:
答:每对对应线段是相等的,平行的。
A
B
C
D
E
F
G
H
∠BAD=∠FEH,∠ABC=∠EFG,
∠BCD=∠FGH,∠ADC=∠EHG
A
B
C
A’
B’
C’
X
Y
(1)??平移后,对应线段_____________
??(2) 平移后,对应角______________
(3)??平移后,对应点的连线段______________
(4) 平移后,新图形和原图形是一对_________
4、经过平移,图形上的每个点都沿着____________移动了________的距离,因此
同一方向
相同
平行且相等
相等
平行且相等
全等图形
A? B? ∥AB,
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.
A? B? =AB,
∠B? =∠B.
同时也有A? C?∥____,
A? C? =_____,
∠C? =_____.
AC
AC
∠C
但不管怎样,我们总可以推得
B? C? 与 BC 有什么关系?
在平移过程中,对应线段也可能在一条直线上。
平移的特征有:
①图形的形状、大小不变,图形的位置发生变化。
②图形上每一点都沿着相同的方向移动了相等的距离。
③对应线段平行(或在一条直线上)并且相等。
④对应角相等。
⑤平移后对应点所连的线段平行(或在一条直线上)且相等。
平移的性质
一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等;对应角相等。
【说明】1.决定平移的因素是平移的方向和距离;
2.平移只改变图形的位置,图形的形状和大小不变.
A
B
1.点的平移作法
将A点沿着射线XY方向平移3cm.
X
Y
【作法】
1.过点A作射线AZ∥XY;
2.在射线AZ上截取线段AB,使AB=3cm;
3.B点即为所求作.
Z
简单的平移作图
A
C
2.线段的平移作法
将线段AB沿着射线XY方向平移3cm.
X
Y
【作法一】
1.将线段的端点A平移,得点C;
2.将线段的端点B平移,得点D;
3.连接CD,线段CD即为所求作.
B
D
【反思】本作法运用了平移的什么性质?
A
C
将线段AB沿着射线XY方向平移3cm.
X
Y
【作法二】
1.将线段的端点A平移,得点C;
2.过C点作线段AB的平行线CZ;
3.在射线CZ上截取线段CD,使CD=AB,则线段CD即为所求作.
B
D
Z
【反思】本作法运用了平移的什么性质?
3.图形的平移作法
如图经过平移,△ABC的顶点A移到了点D.
(1)指出平移的方向和平移距离
(2)作出平移后的三角形.
(2)分别过点B,C作BE,CF平行且等于AD,
连接DE, DF,EF;
B
【反思】本作法运用了平移的什么性质?
C
A
D
E
F
解:(1).连接AD,
平移的方向为射线AD(点A到点D )的方向,平移的距离为线段AD的长度
则△DEF就是△ABC平移后的图形
如果经过平移,△ABC的顶点A移到了点D. 想一想:还有其他作法作出平移后的三角形吗?
B
C
A
D
E
F
M
N
【规律方法】如何进行平移作图?
关键在于按要求(方向和距离)作出对应点.
然后,顺次连接对应点即可.
确定一个图形平移后的位置,需要哪些条件?
平移画图的步骤:
确定一个图形平移后的位置所需要的条件:
原图形的位置;
平移的方向;
平移的距离或一个对应点的位置。
平移不改变图形的形状和大小。经过平移,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移的 定 义
平移的 性 质
平移的作 图
应用平移性质作一些简单平面图形平移后的图形.
掌握“以局部代整体”的平移作图方法.
1.课本67页 习题3.1
2.预习:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
