北师大版七年级数学下册第三章变量之间的关系单元检查试卷含答案
文档属性
| 名称 | 北师大版七年级数学下册第三章变量之间的关系单元检查试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-08 11:09:49 | ||
图片预览

文档简介
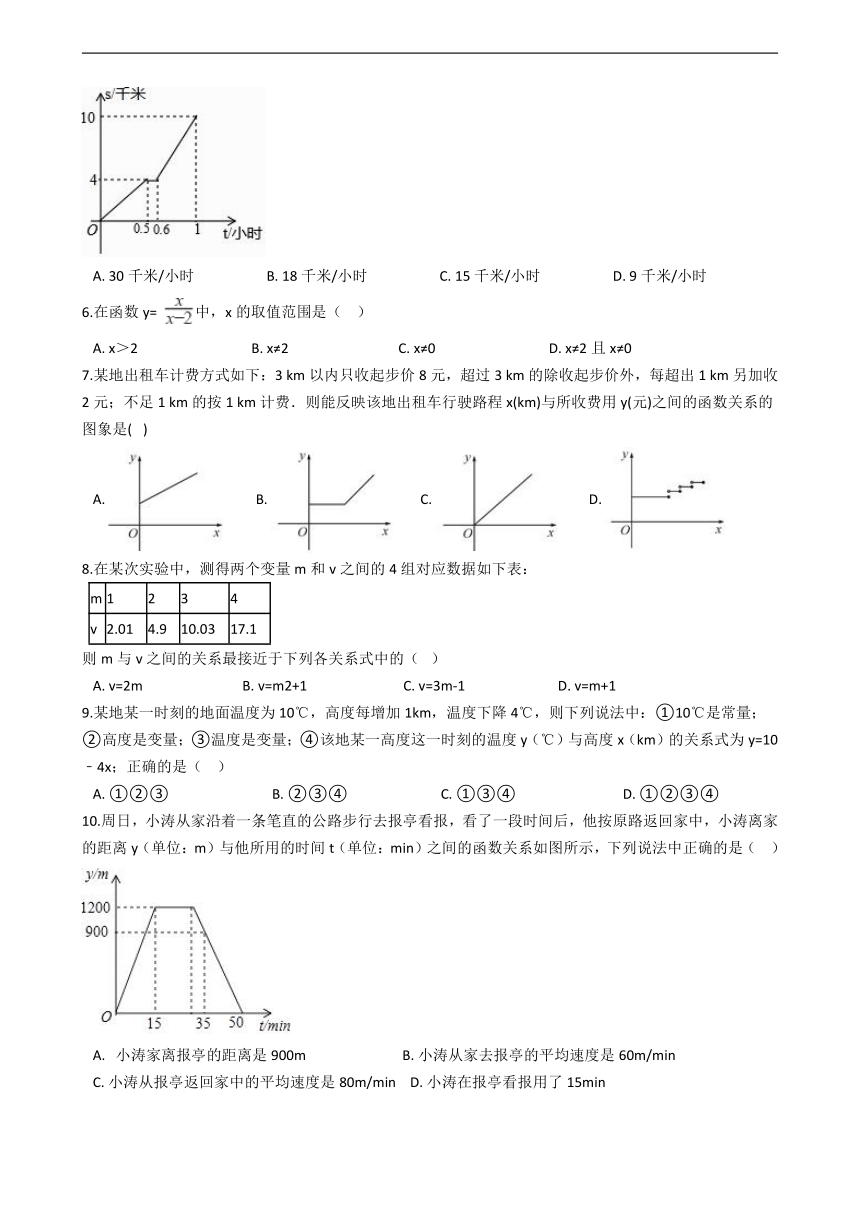
北师大版七年级数学下册第三章变量之间的关系
一、选择题(共10题;共30分)
1.在三角形面积公式S= ah,a=2cm中,下列说法正确的是(??? )
A.?S,a是变量, h是常量?????????????????????????????????????B.?S,h是变量, 是常量
C.?S,h是变量, a是常量?????????????????????????????????????D.?S,h,a是变量, 是常量
2.下列图象不能表示函数关系的是(? ?)
A.??????????B.????????????C.???????????D.?
3.为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列哪个函数图象能近似地刻画上升国旗离旗杆顶端的距离与时间的关系(??? )
A.???????????????????B.??????????????????C.??????????????????D.?
4.均匀地向一个瓶子注水,最后把瓶子注满.在注水过程中,水面高度h随时间t的变化规律如图所示,则这个瓶子的形状是下列的(?? )
?
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
5.周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为(?? )
A.?30千米/小时?????????????????????B.?18千米/小时?????????????????????C.?15千米/小时?????????????????????D.?9千米/小时
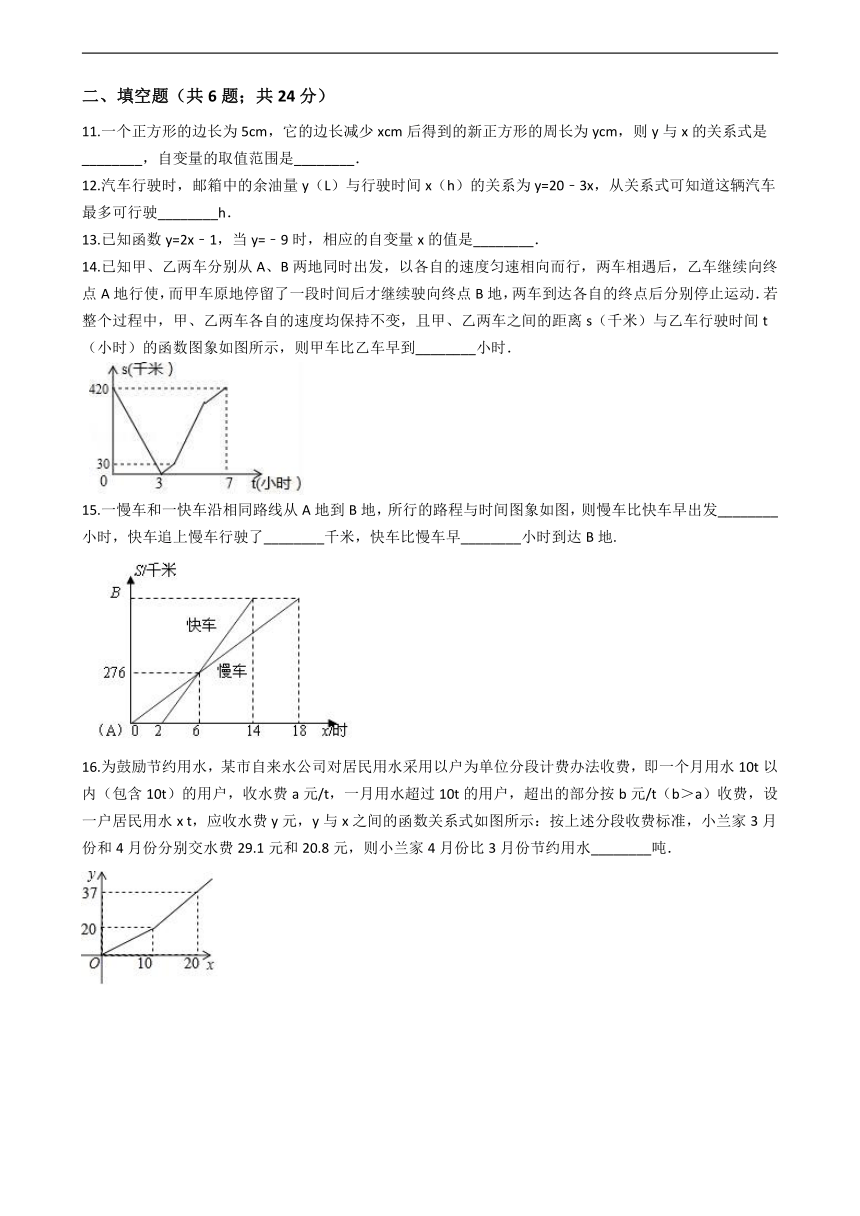
6.在函数y= 中,x的取值范围是(?? )
A.?x>2?????????????????????????????????B.?x≠2????????????????????????????????C.?x≠0?????????????????????????????????D.?x≠2且x≠0
7.某地出租车计费方式如下:3 km以内只收起步价8元,超过3 km的除收起步价外,每超出1 km另加收2元;不足1 km的按1 km计费.则能反映该地出租车行驶路程x(km)与所收费用y(元)之间的函数关系的图象是(? )
A.?????????B.?????????C.????????D.?
8.在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
m 1 2 3 4
v 2.01 4.9 10.03 17.1
则m与v之间的关系最接近于下列各关系式中的(? )
A.?v=2m?????????????????????????????B.?v=m2+1????????????????????????????C.?v=3m-1???????????????????????????D.?v=m+1
9.某地某一时刻的地面温度为10℃,高度每增加1km,温度下降4℃,则下列说法中:①10℃是常量;②高度是变量;③温度是变量;④该地某一高度这一时刻的温度y(℃)与高度x(km)的关系式为y=10﹣4x;正确的是(?? )
A.?①②③??????????????????????????????B.?②③④???????????????????????????C.?①③④???????????????????????????????D.?①②③④
10.周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是(?? )
?小涛家离报亭的距离是900m????????????????????????????B.?小涛从家去报亭的平均速度是60m/min
C.?小涛从报亭返回家中的平均速度是80m/min????D.?小涛在报亭看报用了15min
二、填空题(共6题;共24分)
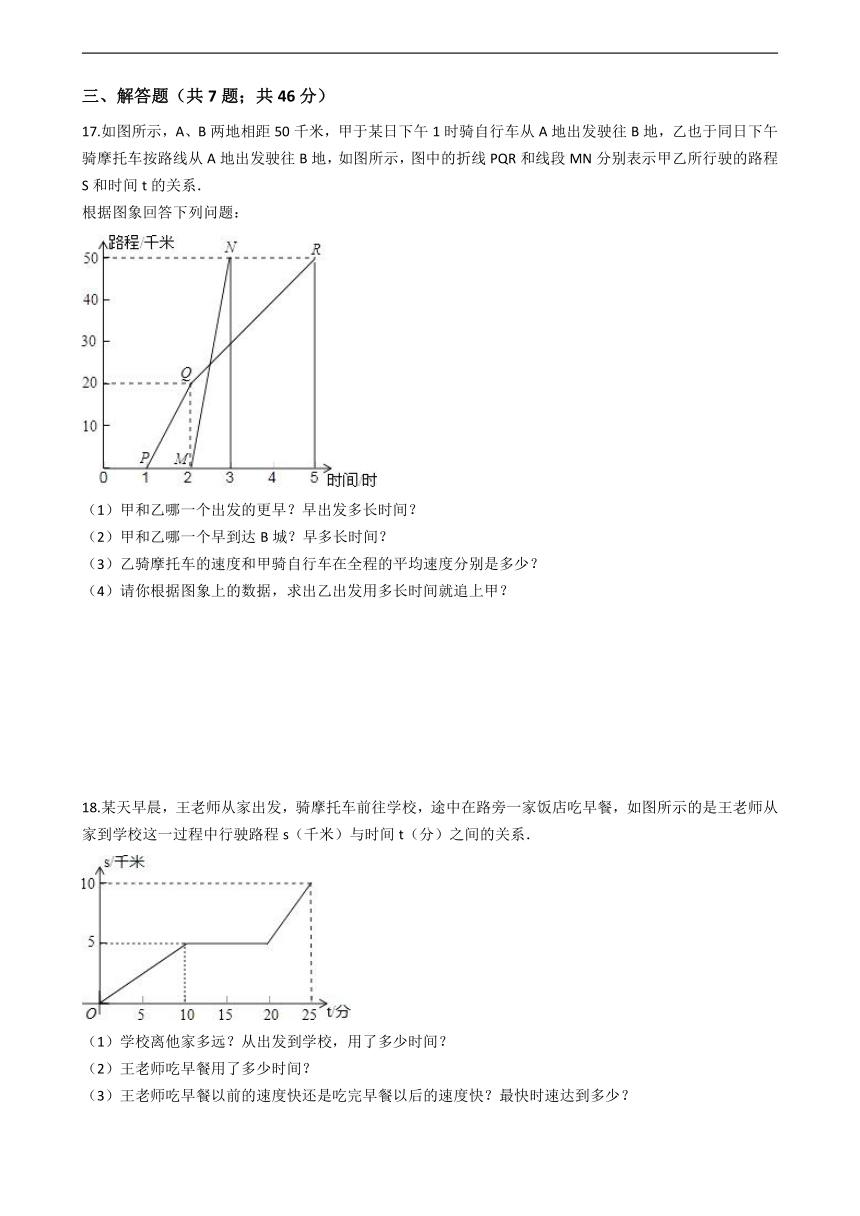
11.一个正方形的边长为5cm,它的边长减少xcm后得到的新正方形的周长为ycm,则y与x的关系式是________,自变量的取值范围是________.
12.汽车行驶时,邮箱中的余油量y(L)与行驶时间x(h)的关系为y=20﹣3x,从关系式可知道这辆汽车最多可行驶________h.
13.已知函数y=2x﹣1,当y=﹣9时,相应的自变量x的值是________.
14.已知甲、乙两车分别从A、B两地同时出发,以各自的速度匀速相向而行,两车相遇后,乙车继续向终点A地行使,而甲车原地停留了一段时间后才继续驶向终点B地,两车到达各自的终点后分别停止运动.若整个过程中,甲、乙两车各自的速度均保持不变,且甲、乙两车之间的距离s(千米)与乙车行驶时间t(小时)的函数图象如图所示,则甲车比乙车早到________小时.
15.一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发________小时,快车追上慢车行驶了________千米,快车比慢车早________小时到达B地.
16.为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,超出的部分按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:按上述分段收费标准,小兰家3月份和4月份分别交水费29.1元和20.8元,则小兰家4月份比3月份节约用水________吨.
三、解答题(共7题;共46分)
17.如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发用多长时间就追上甲?
18.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
19.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
20.钓鱼岛自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.
21.如下表:
n 1 2 3 4 …
y 2×1 4×3 6×5 8×7
试研讨这里的y与n的关系式,并指出其中的变量.
一根80厘米的弹簧,一端固定,如果另一端挂上物体,那么在正常情况下物体的质量每增加1千克可使弹簧增长2厘米
(1)写出弹簧总长度y(厘米)与所挂物体的质量x(千克)之间的数量关系.
(2)若在这根弹簧上挂上某一物体后,弹簧总长为96厘米,求所挂物体的质量?
23.行驶中的汽车,在刹车后由于惯性的作用,还将继续向前滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能(车速不超过140千米/时),对这种汽车进行测试,测得数据如下表:
刹车时车速
(千米/时) 20 40 60 80 100 120
刹车距离(米) 1.0 3.6 7.8 13.6 21 30
回答下列问题:
(1)上表反映了哪两个变量之间的关系?
(2)如果刹车时车速为60千米/时,那么刹车距离是多少米?
答案
一、选择题
1.C 2. A 3. A 4. B 5.C 6. B 7. D 8. B 9. D 10.D
二、填空题
11. y=20-4x;0≤x<5 12. 13.-4 14. 15.2;276;4 16.4.9
三、解答题
17.(1)解:甲下午1时出发,乙下午2时出发,
所以甲更早,早出发1小时
(2)解:甲5时到达,乙3时到达,
所以乙更早,早到2小时
(3)解:乙的速度= =50(千米/小时),
甲的平均速度= =12.5(千米/小时)
(4)解:设乙出发x小时就追上甲,
根据题意得:50x=20+10x,
x=0.5,
答:乙出发0.5小时就追上甲
18.(1)解:依题意得:学校离王老师家有10千米,从出发到学校王老师用了25分钟
(2)解:依题意得:王老师吃早餐用了10分钟
(3)解:吃早餐以前的速度为:5÷10=0.5km/分钟,吃完早餐以后的速度为:(10﹣5)÷(25﹣20)=1km/分钟=60km/小时,
∴王老师吃完早餐以后速度快,最快时速达到60km/小时
19.解:由函数图象,得:
进水管每分钟的进水量为: (升).
设出水管每分钟的出水量为 升,由函数图象,得
.
解得: .
∴ (分钟).
即从关闭进水管起需要8分钟该容器内的水恰好放完
20.解:由图象及题意,得 故障前的速度为:80÷1=80海里/时,
故障后的速度为:(180﹣80)÷1=100海里/时.
设航行额全程有a海里,由题意,得 =2+ ,
解得:a=480,
则原计划行驶的时间为:480÷80=6小时,
解法二:设原计划行驶的时间为t小时,
80t=80+100(t﹣2)
解得:t=6,
故计划准点到达的时刻为:7:00.
21.解:根据表中数据可得y=2n(2n﹣1). 变量是y、n
22.解:(1)弹簧的总长度等于弹簧挂重物伸长的长度加弹簧的长度,得
y=2x+80,
(2)当y=96时,2x+80=96,
?解得x=8,
答:所挂重物的质量是8千克.
23.解:(1)上表反映了刹车速度和刹车距离之间的关系;
(2)根据表格可得:如果刹车时车速为60千米/时,那么刹车距离是7.8米.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
