人教版七年级下册 7.1.2平面直角坐标系课件(共28张ppt)
文档属性
| 名称 | 人教版七年级下册 7.1.2平面直角坐标系课件(共28张ppt) | 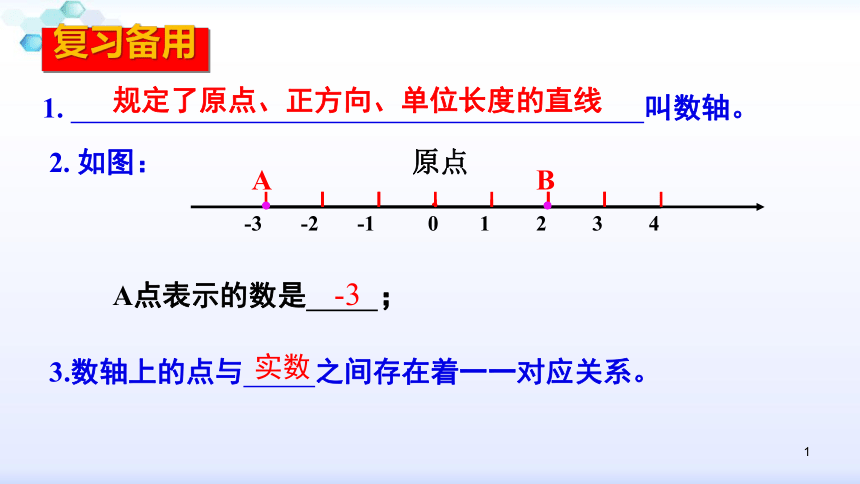 | |
| 格式 | zip | ||
| 文件大小 | 680.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-08 19:49:54 | ||
图片预览








文档简介
1
复习备用
规定了原点、正方向、单位长度的直线
A点表示的数是 ;
3.数轴上的点与 之间存在着一一对应关系。
2. 如图:
-3
实数
1. 叫数轴。
·
0
1
2
3
4
-3
-2
-1
原点
?
?
A
B
2
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为6。反过来,知道数轴上一个点的坐标(如:坐标是4),这个的点在数轴上的位置也就确定了。
A
B
O
如何确定直线上点的位置?
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
?
?
?
C
?
复习备用
3
数轴上的点与实数之间存在着一一对应的关系.
如图:
点B在数轴上的坐标是 ;
点C在数轴上的坐标是 ;
点D在数轴上的坐标是 ;
-1.5
0
2
●
●
●
●
●
A
B
C
D
F
-3 -2 -1 0 1 2 3 4
复习备用
4
激趣导入
如何确定平面上点的位置?
小红
小明
小强
●
●
●
5
人教版七年级数学下册
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.2(1):平面直角坐标系
1.知道平面直角坐标系的有关概念,会画平面直角坐标系.
2.知道平面直角坐标系中点的坐标的意义,能由坐标描点和由点写出坐标.
3.经历点的坐标由一般到特殊的过程,知道特殊点的坐标的特点.
4.在学习过程中,初步体会数形结合思想,
重点:平面直角坐标系的概念,根据坐标描点,由点写坐标.
难点:确定坐标轴上的点的坐标.
6
学习目标
重点难点
7
知识链接
蜘蛛"表演"与直角坐标系
1619年11月的一天,笛卡儿因病躺在床上,他默默地思考着一个问题:通过什么样的办法,才能把“点”和“数"联系起来呢?突然,他看见屋顶角上的一只蜘蛛,蜘蛛顺着丝爬来爬去.蜘蛛的“表演"使笛卡尔的思路豁然开朗.他想,可以把蜘蛛看作一个点,它在网上可以上、下、左、右运动,能不能把蜘蛛的每一个位置用一组数确定下来呢?用一组数(a,b)可以表示平面上的一个点,平面上的一个点也可以用两个有顺序的数来表示,于是在蜘蛛的启示下,笛卡尔创建了直角坐标系.
8
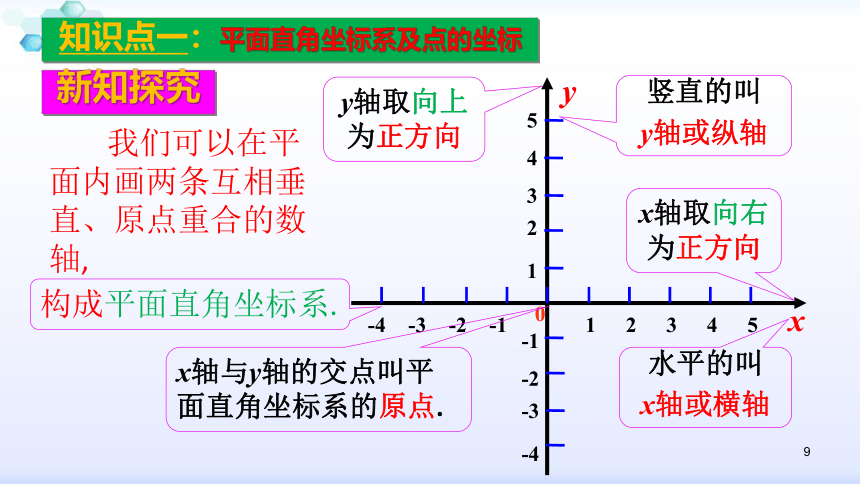
新知探究
知识点一:平面直角坐标系及点的坐标
类似于利用数轴确定直线上点的位置,能不能找到一种方法来确定平面内点的位置呢?
9
新知探究
知识点一:平面直角坐标系及点的坐标
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
我们可以在平面内画两条互相垂直、原点重合的数轴,
构成平面直角坐标系.
水平的叫
x轴或横轴
竖直的叫
y轴或纵轴
y轴取向上为正方向
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
10
新知探究
知识点一:平面直角坐标系及点的坐标
两条数轴:(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般取相同的
请你在本子上画一平面直角坐标系。看谁画的又对又快!并思考:平面直角坐标系具有哪些特征呢?
O
x
y
-3 -2 -1 1 2 3
4
3
2
1
-1
-2
-3
-4
11
学以致用
知识点一:平面直角坐标系及点的坐标
1、下面四个图形中,是平面直角坐标系的是( )
x
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(A)
3 2 1 -1 -2 -3
2
1
-1
-2
x
y
(B)
O
x
y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
x
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
12
新知探究
知识点一:平面直角坐标系及点的坐标
A
B
C
D
x轴
y轴
原点
4
3
2
1
-1
5
-2
-3
-4
0
2
1
5
4
3
-4
-3
-2
-1
例题:如何确定点A的坐标呢?
过A点作y轴的垂线,垂足坐标是4
我们说A点的横坐标是3
A点的纵坐标是4
有序数对(3,4)就叫做A的坐标
记作A(3,4)
过A点作x轴的垂线,垂足坐标是3
你能写出图中点B,C,D,的坐标吗?
13
归纳总结
由点找坐标的方法:过点A分别作x、y轴的垂线,垂足分别为M、N.则点M、N的坐标就是这点的坐标,记为(x,y)
知识点一:平面直角坐标系及点的坐标
14
知识点一:平面直角坐标系及点的坐标
典例讲评
例1 在你的网格本上画出合适的平面直角坐标系,并在平面直角坐标系中描出下列各点:
A(4,5), B(-2,3),C(-4,-1), D(2.5,-2),E(0,-4).
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
.
A(4,5)
.
B(-2,3)
.
C(-4,-1)
.
D(2.5,-2)
.
E(0,-4)
解:如图,先在x轴上找出表示4的点,
再在y轴上找出表示5的点,过这两个
点分别作x轴和y轴的垂线,垂线的交
点就是点A.
类似地,请你在图上描出点B,C, D, E.
15
归纳总结
由坐标找点的方法:先在 x 轴上找出表示横坐标的点,再在 y 轴上找出表示纵坐标的点,过这两个点分别作 x 轴和 y 轴的垂线,垂线的交点就是点A.
知识点一:平面直角坐标系及点的坐标
16
学以致用
知识点一:平面直角坐标系及点的坐标
1.写出图中点A,B,C,D,E,F的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
17
学以致用
知识点一:平面直角坐标系及点的坐标
x
y
O
1 2 3 4 5 6
5
4
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
2.在图中描出下列各点:A(-5,-3), B(4,0), C(-6,2), D(5,-3.5), E(0,5), F(6,2).
A
.
B
.
C
.
D
.
E
.
F
.
先独立完成课本128页复习巩固第1、3题,再相互交流;
18
合作探究
知识点一:平面直角坐标系及点的坐标
19
新知探究
知识点二:坐标轴上点的坐标
思考:原点O的坐标是什么?
x轴和y轴上的点的坐标有什么特点?
x
y
O
1 2 3 4 5 6
5
4
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
在x轴上的点,
纵坐标等于0.
在y轴上的点,
横坐标等于0.
20
典例讲评
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
例2、已知点P到x轴的距离为2,到y轴的距离为1.如果过点P作两坐标轴的垂线,垂足分别在x轴的正半轴上和y轴的负半轴上,那么点P的坐标是( )
A.(2,-1) B.(1,-2)
C.(-2,-1) D.(1,2)
知识点二:坐标轴上点的坐标
B
21
新知探究
知识点二:坐标轴上点的坐标
解析:由点P到x轴的距离为2,可知点P的纵坐标的绝对值为2,又因为垂足在y轴的负半轴上,则纵坐标为-2;由点P到y轴的距离为1,可知点P的横坐标的绝对值为1,又因为垂足在x轴的正半轴上,则横坐标为1.故点P的坐标是(1,-2).
22
归纳总结
知识点二:坐标轴上点的坐标
此类题的易错点有三处:
①混淆距离与坐标之间的区别;
②不知道“点P到x轴的距离”对应的是纵坐标,“点P到y轴的距离”对应的是横坐标;
③忽略坐标的符号出现错解.若本例题只已知距离而无附加条件,则点P的坐标有四个.
23
学以致用
知识点二:坐标轴上点的坐标
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
2、在平面直角坐标系中,点P(-3,4)到x轴的距离为( )
A.3 B. -3 C.4 D. -4
C
24
归纳总结
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
知识点二:坐标轴上点的坐标
A
P(x,y)
B
C
D
如图:点A、B、C、D到x轴和y轴的距离分别是多少?
如果点P的坐标是(x,y),则点P到x轴的距离= ;
到y轴的距离= ;
∣x ∣
∣y ∣
先独立完成导学案互动探究2、3、4,再同桌相互交流,最后小组交流;
25
合作探究
知识点二:坐标轴上点的坐标
26
思维导图
平面直角坐标系
平面内的点(x,y)到x 轴的距离 ,
到y 轴的距离 ,
x轴上的点 坐标为0
y轴上的点 坐标为0
坐标平面内的点表示:是有序数对即:坐标
组成:在平面内画两条互相 、
原点 数轴
27
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
28
1.课本第68页:练习1、2习题7.1第3、4、7题;
2.《导学测评》第18页;
作业布置
复习备用
规定了原点、正方向、单位长度的直线
A点表示的数是 ;
3.数轴上的点与 之间存在着一一对应关系。
2. 如图:
-3
实数
1. 叫数轴。
·
0
1
2
3
4
-3
-2
-1
原点
?
?
A
B
2
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为6。反过来,知道数轴上一个点的坐标(如:坐标是4),这个的点在数轴上的位置也就确定了。
A
B
O
如何确定直线上点的位置?
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
?
?
?
C
?
复习备用
3
数轴上的点与实数之间存在着一一对应的关系.
如图:
点B在数轴上的坐标是 ;
点C在数轴上的坐标是 ;
点D在数轴上的坐标是 ;
-1.5
0
2
●
●
●
●
●
A
B
C
D
F
-3 -2 -1 0 1 2 3 4
复习备用
4
激趣导入
如何确定平面上点的位置?
小红
小明
小强
●
●
●
5
人教版七年级数学下册
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.2(1):平面直角坐标系
1.知道平面直角坐标系的有关概念,会画平面直角坐标系.
2.知道平面直角坐标系中点的坐标的意义,能由坐标描点和由点写出坐标.
3.经历点的坐标由一般到特殊的过程,知道特殊点的坐标的特点.
4.在学习过程中,初步体会数形结合思想,
重点:平面直角坐标系的概念,根据坐标描点,由点写坐标.
难点:确定坐标轴上的点的坐标.
6
学习目标
重点难点
7
知识链接
蜘蛛"表演"与直角坐标系
1619年11月的一天,笛卡儿因病躺在床上,他默默地思考着一个问题:通过什么样的办法,才能把“点”和“数"联系起来呢?突然,他看见屋顶角上的一只蜘蛛,蜘蛛顺着丝爬来爬去.蜘蛛的“表演"使笛卡尔的思路豁然开朗.他想,可以把蜘蛛看作一个点,它在网上可以上、下、左、右运动,能不能把蜘蛛的每一个位置用一组数确定下来呢?用一组数(a,b)可以表示平面上的一个点,平面上的一个点也可以用两个有顺序的数来表示,于是在蜘蛛的启示下,笛卡尔创建了直角坐标系.
8
新知探究
知识点一:平面直角坐标系及点的坐标
类似于利用数轴确定直线上点的位置,能不能找到一种方法来确定平面内点的位置呢?
9
新知探究
知识点一:平面直角坐标系及点的坐标
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
我们可以在平面内画两条互相垂直、原点重合的数轴,
构成平面直角坐标系.
水平的叫
x轴或横轴
竖直的叫
y轴或纵轴
y轴取向上为正方向
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
10
新知探究
知识点一:平面直角坐标系及点的坐标
两条数轴:(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般取相同的
请你在本子上画一平面直角坐标系。看谁画的又对又快!并思考:平面直角坐标系具有哪些特征呢?
O
x
y
-3 -2 -1 1 2 3
4
3
2
1
-1
-2
-3
-4
11
学以致用
知识点一:平面直角坐标系及点的坐标
1、下面四个图形中,是平面直角坐标系的是( )
x
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(A)
3 2 1 -1 -2 -3
2
1
-1
-2
x
y
(B)
O
x
y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
x
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
12
新知探究
知识点一:平面直角坐标系及点的坐标
A
B
C
D
x轴
y轴
原点
4
3
2
1
-1
5
-2
-3
-4
0
2
1
5
4
3
-4
-3
-2
-1
例题:如何确定点A的坐标呢?
过A点作y轴的垂线,垂足坐标是4
我们说A点的横坐标是3
A点的纵坐标是4
有序数对(3,4)就叫做A的坐标
记作A(3,4)
过A点作x轴的垂线,垂足坐标是3
你能写出图中点B,C,D,的坐标吗?
13
归纳总结
由点找坐标的方法:过点A分别作x、y轴的垂线,垂足分别为M、N.则点M、N的坐标就是这点的坐标,记为(x,y)
知识点一:平面直角坐标系及点的坐标
14
知识点一:平面直角坐标系及点的坐标
典例讲评
例1 在你的网格本上画出合适的平面直角坐标系,并在平面直角坐标系中描出下列各点:
A(4,5), B(-2,3),C(-4,-1), D(2.5,-2),E(0,-4).
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
.
A(4,5)
.
B(-2,3)
.
C(-4,-1)
.
D(2.5,-2)
.
E(0,-4)
解:如图,先在x轴上找出表示4的点,
再在y轴上找出表示5的点,过这两个
点分别作x轴和y轴的垂线,垂线的交
点就是点A.
类似地,请你在图上描出点B,C, D, E.
15
归纳总结
由坐标找点的方法:先在 x 轴上找出表示横坐标的点,再在 y 轴上找出表示纵坐标的点,过这两个点分别作 x 轴和 y 轴的垂线,垂线的交点就是点A.
知识点一:平面直角坐标系及点的坐标
16
学以致用
知识点一:平面直角坐标系及点的坐标
1.写出图中点A,B,C,D,E,F的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
17
学以致用
知识点一:平面直角坐标系及点的坐标
x
y
O
1 2 3 4 5 6
5
4
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
2.在图中描出下列各点:A(-5,-3), B(4,0), C(-6,2), D(5,-3.5), E(0,5), F(6,2).
A
.
B
.
C
.
D
.
E
.
F
.
先独立完成课本128页复习巩固第1、3题,再相互交流;
18
合作探究
知识点一:平面直角坐标系及点的坐标
19
新知探究
知识点二:坐标轴上点的坐标
思考:原点O的坐标是什么?
x轴和y轴上的点的坐标有什么特点?
x
y
O
1 2 3 4 5 6
5
4
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
在x轴上的点,
纵坐标等于0.
在y轴上的点,
横坐标等于0.
20
典例讲评
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
例2、已知点P到x轴的距离为2,到y轴的距离为1.如果过点P作两坐标轴的垂线,垂足分别在x轴的正半轴上和y轴的负半轴上,那么点P的坐标是( )
A.(2,-1) B.(1,-2)
C.(-2,-1) D.(1,2)
知识点二:坐标轴上点的坐标
B
21
新知探究
知识点二:坐标轴上点的坐标
解析:由点P到x轴的距离为2,可知点P的纵坐标的绝对值为2,又因为垂足在y轴的负半轴上,则纵坐标为-2;由点P到y轴的距离为1,可知点P的横坐标的绝对值为1,又因为垂足在x轴的正半轴上,则横坐标为1.故点P的坐标是(1,-2).
22
归纳总结
知识点二:坐标轴上点的坐标
此类题的易错点有三处:
①混淆距离与坐标之间的区别;
②不知道“点P到x轴的距离”对应的是纵坐标,“点P到y轴的距离”对应的是横坐标;
③忽略坐标的符号出现错解.若本例题只已知距离而无附加条件,则点P的坐标有四个.
23
学以致用
知识点二:坐标轴上点的坐标
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
2、在平面直角坐标系中,点P(-3,4)到x轴的距离为( )
A.3 B. -3 C.4 D. -4
C
24
归纳总结
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
知识点二:坐标轴上点的坐标
A
P(x,y)
B
C
D
如图:点A、B、C、D到x轴和y轴的距离分别是多少?
如果点P的坐标是(x,y),则点P到x轴的距离= ;
到y轴的距离= ;
∣x ∣
∣y ∣
先独立完成导学案互动探究2、3、4,再同桌相互交流,最后小组交流;
25
合作探究
知识点二:坐标轴上点的坐标
26
思维导图
平面直角坐标系
平面内的点(x,y)到x 轴的距离 ,
到y 轴的距离 ,
x轴上的点 坐标为0
y轴上的点 坐标为0
坐标平面内的点表示:是有序数对即:坐标
组成:在平面内画两条互相 、
原点 数轴
27
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
28
1.课本第68页:练习1、2习题7.1第3、4、7题;
2.《导学测评》第18页;
作业布置
