【鲁教版八下精美学案】9.3 相似多边形(知识构建+考点归纳+真题训练)
文档属性
| 名称 | 【鲁教版八下精美学案】9.3 相似多边形(知识构建+考点归纳+真题训练) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-09 00:00:00 | ||
图片预览




文档简介
第九章 图形的相似
第3节 相似多边形
知 识 梳 理
知识点1 相似多边形
两个多边形的___________相同,各角________、各边________,这样的两个多边形叫做相似多边形。
注意(1)相似多边形是指这两个多边形仅仅形状相同,大小不一定相同,其中一个图形可以看成是由另一个图形按一定的比例放大或缩小而成的。(2)相似多边形的读写法:在表示两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上如:五边形 ABCDE与五边形A1B1C1D1E1相似,记作:五边形 ABCDE∽五边形A1B1C1D1E1,“∽”读作“相似于”。(3)相似多边形必须同时具备两个条件:对应角相等,对应边成比例,两者缺一不可,仅有对应角都相等或仅有对应边成比例的两个多边形并不一定相似,两个边数不同的多边形一定不相似。
知识点2 相似比
相似多边形__________的比叫相似比。
注意(1)相似多边形的相似比具有顺序性,如五边形 ABCDE∽五边形A1B1C1D1E1,若,则五边形 ABCDE与五边形A1B1C1D1E1的相似比k1=,而五边形A1B1C1D1E1与五边形 ABCDE的相似比k2=。(2)全等多边形一定是相似多边形,但相似多边形不一定全等。(3)若两个多边形全等,则其相似比为1。
知识点3 相似多边形的性质
相似多边形的__________________,_________________。
几何语言:如图所示,
∵五边形 ABCDE∽五边形A1B1C1D1E1,∴∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E=∠E1,。
考 点 突 破
考点1:相似多边形的定义
典例1下列结论正确的是( )
A.两个正方形一定相似 B.两个菱形一定相似
C.两个等腰梯形一定相似 D.两个直角梯形一定相似
思路导析:根据相似多边形的概念对各个选项进行判断即可。
∵两个正方形对应角相等,对应边的比相等,∴两个正方形一定相似,A正确;
∵两个菱形的对应角不一定相等,∴两个菱形不一定相似,B不正确;
∵两个等腰梯形对应角不一定相等,对应边的比不一定相等,∴两个等腰梯形不一定相似,C不正确;
∵两个直角梯形对应角不一定相等,对应边的比不一定相等,∴两个直角梯形不一定相似,D不正确,
答案:A
友情提示 (1)相似多边形的特征是识别两个多边形是否相似的方法,判断两个多边形相似的方法:①判断对应角是否相等,对应边是否成比例;②下结论,若①中两个条件都成立,则两个多边形相似,否则不相似.(2)常见的相似多边形总结:①所有的正三角形都相似;②所有的正方形都相似;③所有的等腰直角三角形都相似;④所有的正六边形都相似。
变式1 如图所示的三个矩形中,是相似的是( )
A.甲与乙 B.乙与丙 C.甲与丙 D.甲乙丙都相似
变式2 有下列各组的两个图形:
①两个等腰三角形;②两个矩形;③两个等边三角形;④两个正方形;⑤各有一个内角是45o的两个等腰三角形。
其中一定相似的是___________(只填序号)。
考点2:相似多边形的相似比
典例2 如图所示,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4。
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比。
思路导析:(1)矩形DMNC与矩形ABCD相似,对应边的比相等,就可以得到AD的长;(2)相似比即是对应边的比。
解:(1)由已知得MN=AB,MD=AD=BC。
∵矩形DMNC与矩形ABCD相似,∴。
∵MN=AB,DM=AD, BC=AD,∴AD2=AB2,由AB=4,得AD=4。
(2)由(1)得DM=AD=2。
∴矩形DMNC与矩形ABCD的相似比为。
解题归纳 根据相似多边形的性质可知对应边的比相等。
变式3 如图所示,一张矩形纸片ABCD的长AB=a,宽BC=b,将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
A.2:1 B.:1 C.3: D.3:2
变式4 两个相似多边形的最长边分别是10和30,其中一多边形的最短边为6,则另一多边形的最短边为____________。
考点3:相似多边形性质的应用
典例3 如图所示,四边形ABCD四边形∽EFGH,∠A=90°,∠B=75°,∠E=90°,∠H=105°,AD=18,EF=4,FG=4,EH=4.求∠G的度数和AB,BC的长。
思路导析:根据相似多边形的对应角相等,对应边成比例,再结合四边形的内角和等于360°,可以求解。
解:∵四边形ABCD∽四边形EFGH,
∴∠A=∠E=90°,∠B=∠F=75°,∠D=∠H=105°。
又由∠E+∠F+∠G+∠H=360°,得∠G=90°。
又由,得,解得AB=18,BC=18,
∴∠G=90°,AB=18,BC=18.
友情提示 找准相似多边形的对应边是解决此类问题的关键,方法类似于找全等三角形对应边和对应角的方法。
变式5 如图所示,四边形ABCD∽四边形A'B'C′D′求边x,y的长度和角a的大小。
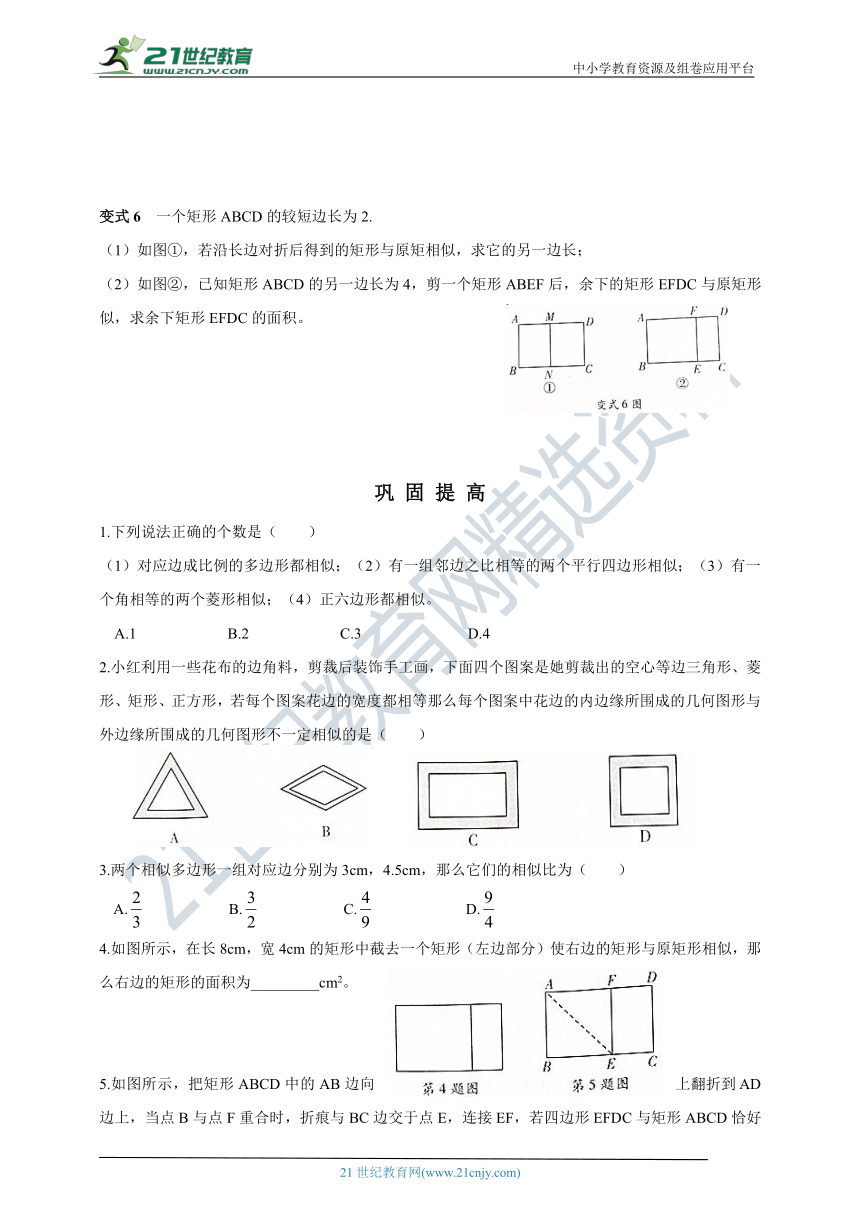
变式6 一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪一个矩形ABEF后,余下的矩形EFDC与原矩形似,求余下矩形EFDC的面积。
巩 固 提 高
1.下列说法正确的个数是( )
(1)对应边成比例的多边形都相似;(2)有一组邻边之比相等的两个平行四边形相似;(3)有一个角相等的两个菱形相似;(4)正六边形都相似。
A.1 B.2 C.3 D.4
2.小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心等边三角形、菱形、矩形、正方形,若每个图案花边的宽度都相等那么每个图案中花边的内边缘所围成的几何图形与外边缘所围成的几何图形不一定相似的是( )
3.两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为( )
A. B. C. D.
4.如图所示,在长8cm,宽4cm的矩形中截去一个矩形(左边部分)使右边的矩形与原矩形相似,那 么右边的矩形的面积为_________cm2。
5.如图所示,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为_________。
6.如图所示,菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E和F(点E在点F的左侧),且要使四边形DEBF与菱形ABCD相似,则AE的长为___________。
7.两个相似多边形的相似比是3:7,其中一个多边形的最长边是21,则另一个多边形的最长边是_____。
8.如图所示,四边形ABCD中,AD∥BC,E是AB上一点,EF∥BC交CD于F,若AD=2,BC=4.5,当AE:EB等于多少时,EF分四边形ABCD所成的两个小四边形相似?
9.在AB=30m,AD=20m的矩形花坛四周修筑小路。
(1)如果四周的小路的宽均相等,都是x,如图1所示,那么小路四周所围成的矩形A1B1C1D1和矩形ABCD相似吗?请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x,y,如图2所示,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A′B′C'D'和矩形ABCD相似?请说明理由。
10.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试说明你的理由。
11.如图所示,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为,连接CF,求CF的长。
12.如图所示,点E是菱形ABCD对角线CA的延线上任意一点,以线段AE为边作一个菱AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD。
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=,求GD的长。
真 题 训 练
1.(2018·重庆)制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
2.(2015·盐锦)如图所示,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )
A.2 B.2.4 C.2.5 D.0.3
3.(扬州中考)如图所示,有两个形状相同的星星图案,则x的值为( )
A.15 B.12 C.10 D.8
4.(2018·绥化)在长8cm,宽6cm的矩形中,截去一个矩形,使留下的矩形与原矩形相似,那么留下的矩形面积是________ cm2。
5.(2017·河南)如图所示,四边形ABCD为平行边形,AE平分∠BAD交BC于点E,过点EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长。
参考答案及解析
知识梳理
知识点1:形状 对应相等 对应成比例
知识点2:对应边
知识点3:对应角相等 对应边成比例
考点突破
1.B 2.③④ 3.B 4.2或18
5.解:∵四边形ABCD∽四边形A′B′C′D′,∴,∠A=∠A′=62°,
∠B=∠B′=75°,∠D=∠D′=140°。
∴,∠a = 83o。解得y=,x=12.
∴x=12,y=,∠a=83°。
6.解:(1)由已知得MN=AB=2,MD=AD=BC.
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,。
∴DM·BC=AB·MN,即BC2=4.∴BC=2,即它的另一边长为2;
(2)∵矩形EFDC与原矩形ABCD相似,∴.
∵AB=CD=2,BC=4,∴=1.
∴矩形EFDC的面积=CD·DF=2×1=2。
巩固提高
1.B 2.C 3.A 4.8 5. 6. 7.49或9
8.解:∵EF把梯形ABCD分成两个相似的小梯形,∴梯形 ADFE∽梯形EFCB,∴ 。
∵AD=2,BC=4.5,∴EF=3,∴相似比为。∴AE:EB=2:3。
∴当AE:EB等于2:3时,EF分四边形ABCD所成的两个小四边形相似。
9.解:(1)如果四周的小路的宽均相等,那么小路四周所围成的矩形A1B1C1D1和矩形ABCD不相似.
理由:设四周的小路的宽为x,
∵,,,
?小路四周所围成的矩形A1B1C1D1和矩形ABCD不相似;
(2)当时,小路四周所围成的矩形A'B'C'D'和矩形ABCD相似,
解得,∴路的宽x与y的比值为2:3时,能使小路四周所围成的矩形A'B'C"D'和矩形ABCD相似。
10.解:(1)设每块矩形地砖的长为acm,宽为bcm,
由图可知解得∴矩形地砖的长为45cm,宽为15 cm.
(2)不相似.理由如下:
∵铺成的每部分矩形地面的长为2a=2×45=90(cm),宽为60cm,
∴长与宽的比为,而,
∴铺成的每部分矩形地面的长与宽和地砖的长与宽不成比例,∴它们不相似。
11.解:延长GF交BC于M,
∵四边形AEFG和ABCD是矩形,∴GF∥AE。∵AB⊥BC,GM⊥BC.
分两种情况:
①当AD与AG对应时,∵相似比为,∴。
∵AB=12,AD=BC=9,∴EF=AG=BM=6,GF=AE=8,
∴FM=12-8=4,CM=9-6=3。
在Rt△CMF中,由勾股定理得CF = =5。
②当AD与AE对应时,∵相似比为,∴。
∴。∴ AG=8,AE = 6。∴FM=12-6=6,CM=9-8=1。
在Rt△CMF中,由勾股定理得CF =,
综上所述,CF的长为5或。
12.解:(1)证明:?菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD。
∴∠EAG+∠GAB=∠BAD+∠GAB。∴∠EAB=∠GAD。
∵AE=AG,AB=AD,∴△AEB≌△AGD。∴EB=GD。
(2)如图,连接BD交AC于点P,则BD⊥AC,
∵∠DAB=60°,∴∠PAB=30°。
∴BP =AB=1,AP==。
∵AE=AG=,∴EP=2.
∴EB=。∴ GD=。
真题训练
1.C 2.A 3.D 4.27
5.解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD。
∴∠FAE=∠AEB。∵EF∥AB,∴四边形ABEF是平行四边形.
∵AE平分∠BAD,∴∠FAE=∠BAE。∴∠BAE=∠AEB.
∴AB=EB.∴四边形ABEF是菱形。∴BF平分∠ABC;
(2)∵四边形ABEF为菱形;∴BE=AB=6.∵四边形ABCD∽四边形CEFD,
∴,即。
解得BC=3±3(负值舍去),∴BC=3+3.
第3节 相似多边形
知 识 梳 理
知识点1 相似多边形
两个多边形的___________相同,各角________、各边________,这样的两个多边形叫做相似多边形。
注意(1)相似多边形是指这两个多边形仅仅形状相同,大小不一定相同,其中一个图形可以看成是由另一个图形按一定的比例放大或缩小而成的。(2)相似多边形的读写法:在表示两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上如:五边形 ABCDE与五边形A1B1C1D1E1相似,记作:五边形 ABCDE∽五边形A1B1C1D1E1,“∽”读作“相似于”。(3)相似多边形必须同时具备两个条件:对应角相等,对应边成比例,两者缺一不可,仅有对应角都相等或仅有对应边成比例的两个多边形并不一定相似,两个边数不同的多边形一定不相似。
知识点2 相似比
相似多边形__________的比叫相似比。
注意(1)相似多边形的相似比具有顺序性,如五边形 ABCDE∽五边形A1B1C1D1E1,若,则五边形 ABCDE与五边形A1B1C1D1E1的相似比k1=,而五边形A1B1C1D1E1与五边形 ABCDE的相似比k2=。(2)全等多边形一定是相似多边形,但相似多边形不一定全等。(3)若两个多边形全等,则其相似比为1。
知识点3 相似多边形的性质
相似多边形的__________________,_________________。
几何语言:如图所示,
∵五边形 ABCDE∽五边形A1B1C1D1E1,∴∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E=∠E1,。
考 点 突 破
考点1:相似多边形的定义
典例1下列结论正确的是( )
A.两个正方形一定相似 B.两个菱形一定相似
C.两个等腰梯形一定相似 D.两个直角梯形一定相似
思路导析:根据相似多边形的概念对各个选项进行判断即可。
∵两个正方形对应角相等,对应边的比相等,∴两个正方形一定相似,A正确;
∵两个菱形的对应角不一定相等,∴两个菱形不一定相似,B不正确;
∵两个等腰梯形对应角不一定相等,对应边的比不一定相等,∴两个等腰梯形不一定相似,C不正确;
∵两个直角梯形对应角不一定相等,对应边的比不一定相等,∴两个直角梯形不一定相似,D不正确,
答案:A
友情提示 (1)相似多边形的特征是识别两个多边形是否相似的方法,判断两个多边形相似的方法:①判断对应角是否相等,对应边是否成比例;②下结论,若①中两个条件都成立,则两个多边形相似,否则不相似.(2)常见的相似多边形总结:①所有的正三角形都相似;②所有的正方形都相似;③所有的等腰直角三角形都相似;④所有的正六边形都相似。
变式1 如图所示的三个矩形中,是相似的是( )
A.甲与乙 B.乙与丙 C.甲与丙 D.甲乙丙都相似
变式2 有下列各组的两个图形:
①两个等腰三角形;②两个矩形;③两个等边三角形;④两个正方形;⑤各有一个内角是45o的两个等腰三角形。
其中一定相似的是___________(只填序号)。
考点2:相似多边形的相似比
典例2 如图所示,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4。
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比。
思路导析:(1)矩形DMNC与矩形ABCD相似,对应边的比相等,就可以得到AD的长;(2)相似比即是对应边的比。
解:(1)由已知得MN=AB,MD=AD=BC。
∵矩形DMNC与矩形ABCD相似,∴。
∵MN=AB,DM=AD, BC=AD,∴AD2=AB2,由AB=4,得AD=4。
(2)由(1)得DM=AD=2。
∴矩形DMNC与矩形ABCD的相似比为。
解题归纳 根据相似多边形的性质可知对应边的比相等。
变式3 如图所示,一张矩形纸片ABCD的长AB=a,宽BC=b,将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
A.2:1 B.:1 C.3: D.3:2
变式4 两个相似多边形的最长边分别是10和30,其中一多边形的最短边为6,则另一多边形的最短边为____________。
考点3:相似多边形性质的应用
典例3 如图所示,四边形ABCD四边形∽EFGH,∠A=90°,∠B=75°,∠E=90°,∠H=105°,AD=18,EF=4,FG=4,EH=4.求∠G的度数和AB,BC的长。
思路导析:根据相似多边形的对应角相等,对应边成比例,再结合四边形的内角和等于360°,可以求解。
解:∵四边形ABCD∽四边形EFGH,
∴∠A=∠E=90°,∠B=∠F=75°,∠D=∠H=105°。
又由∠E+∠F+∠G+∠H=360°,得∠G=90°。
又由,得,解得AB=18,BC=18,
∴∠G=90°,AB=18,BC=18.
友情提示 找准相似多边形的对应边是解决此类问题的关键,方法类似于找全等三角形对应边和对应角的方法。
变式5 如图所示,四边形ABCD∽四边形A'B'C′D′求边x,y的长度和角a的大小。
变式6 一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪一个矩形ABEF后,余下的矩形EFDC与原矩形似,求余下矩形EFDC的面积。
巩 固 提 高
1.下列说法正确的个数是( )
(1)对应边成比例的多边形都相似;(2)有一组邻边之比相等的两个平行四边形相似;(3)有一个角相等的两个菱形相似;(4)正六边形都相似。
A.1 B.2 C.3 D.4
2.小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心等边三角形、菱形、矩形、正方形,若每个图案花边的宽度都相等那么每个图案中花边的内边缘所围成的几何图形与外边缘所围成的几何图形不一定相似的是( )
3.两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为( )
A. B. C. D.
4.如图所示,在长8cm,宽4cm的矩形中截去一个矩形(左边部分)使右边的矩形与原矩形相似,那 么右边的矩形的面积为_________cm2。
5.如图所示,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为_________。
6.如图所示,菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E和F(点E在点F的左侧),且要使四边形DEBF与菱形ABCD相似,则AE的长为___________。
7.两个相似多边形的相似比是3:7,其中一个多边形的最长边是21,则另一个多边形的最长边是_____。
8.如图所示,四边形ABCD中,AD∥BC,E是AB上一点,EF∥BC交CD于F,若AD=2,BC=4.5,当AE:EB等于多少时,EF分四边形ABCD所成的两个小四边形相似?
9.在AB=30m,AD=20m的矩形花坛四周修筑小路。
(1)如果四周的小路的宽均相等,都是x,如图1所示,那么小路四周所围成的矩形A1B1C1D1和矩形ABCD相似吗?请说明理由;
(2)如果相对着的两条小路的宽均相等,宽度分别为x,y,如图2所示,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形A′B′C'D'和矩形ABCD相似?请说明理由。
10.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试说明你的理由。
11.如图所示,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为,连接CF,求CF的长。
12.如图所示,点E是菱形ABCD对角线CA的延线上任意一点,以线段AE为边作一个菱AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD。
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=,求GD的长。
真 题 训 练
1.(2018·重庆)制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
2.(2015·盐锦)如图所示,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )
A.2 B.2.4 C.2.5 D.0.3
3.(扬州中考)如图所示,有两个形状相同的星星图案,则x的值为( )
A.15 B.12 C.10 D.8
4.(2018·绥化)在长8cm,宽6cm的矩形中,截去一个矩形,使留下的矩形与原矩形相似,那么留下的矩形面积是________ cm2。
5.(2017·河南)如图所示,四边形ABCD为平行边形,AE平分∠BAD交BC于点E,过点EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长。
参考答案及解析
知识梳理
知识点1:形状 对应相等 对应成比例
知识点2:对应边
知识点3:对应角相等 对应边成比例
考点突破
1.B 2.③④ 3.B 4.2或18
5.解:∵四边形ABCD∽四边形A′B′C′D′,∴,∠A=∠A′=62°,
∠B=∠B′=75°,∠D=∠D′=140°。
∴,∠a = 83o。解得y=,x=12.
∴x=12,y=,∠a=83°。
6.解:(1)由已知得MN=AB=2,MD=AD=BC.
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,。
∴DM·BC=AB·MN,即BC2=4.∴BC=2,即它的另一边长为2;
(2)∵矩形EFDC与原矩形ABCD相似,∴.
∵AB=CD=2,BC=4,∴=1.
∴矩形EFDC的面积=CD·DF=2×1=2。
巩固提高
1.B 2.C 3.A 4.8 5. 6. 7.49或9
8.解:∵EF把梯形ABCD分成两个相似的小梯形,∴梯形 ADFE∽梯形EFCB,∴ 。
∵AD=2,BC=4.5,∴EF=3,∴相似比为。∴AE:EB=2:3。
∴当AE:EB等于2:3时,EF分四边形ABCD所成的两个小四边形相似。
9.解:(1)如果四周的小路的宽均相等,那么小路四周所围成的矩形A1B1C1D1和矩形ABCD不相似.
理由:设四周的小路的宽为x,
∵,,,
?小路四周所围成的矩形A1B1C1D1和矩形ABCD不相似;
(2)当时,小路四周所围成的矩形A'B'C'D'和矩形ABCD相似,
解得,∴路的宽x与y的比值为2:3时,能使小路四周所围成的矩形A'B'C"D'和矩形ABCD相似。
10.解:(1)设每块矩形地砖的长为acm,宽为bcm,
由图可知解得∴矩形地砖的长为45cm,宽为15 cm.
(2)不相似.理由如下:
∵铺成的每部分矩形地面的长为2a=2×45=90(cm),宽为60cm,
∴长与宽的比为,而,
∴铺成的每部分矩形地面的长与宽和地砖的长与宽不成比例,∴它们不相似。
11.解:延长GF交BC于M,
∵四边形AEFG和ABCD是矩形,∴GF∥AE。∵AB⊥BC,GM⊥BC.
分两种情况:
①当AD与AG对应时,∵相似比为,∴。
∵AB=12,AD=BC=9,∴EF=AG=BM=6,GF=AE=8,
∴FM=12-8=4,CM=9-6=3。
在Rt△CMF中,由勾股定理得CF = =5。
②当AD与AE对应时,∵相似比为,∴。
∴。∴ AG=8,AE = 6。∴FM=12-6=6,CM=9-8=1。
在Rt△CMF中,由勾股定理得CF =,
综上所述,CF的长为5或。
12.解:(1)证明:?菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD。
∴∠EAG+∠GAB=∠BAD+∠GAB。∴∠EAB=∠GAD。
∵AE=AG,AB=AD,∴△AEB≌△AGD。∴EB=GD。
(2)如图,连接BD交AC于点P,则BD⊥AC,
∵∠DAB=60°,∴∠PAB=30°。
∴BP =AB=1,AP==。
∵AE=AG=,∴EP=2.
∴EB=。∴ GD=。
真题训练
1.C 2.A 3.D 4.27
5.解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD。
∴∠FAE=∠AEB。∵EF∥AB,∴四边形ABEF是平行四边形.
∵AE平分∠BAD,∴∠FAE=∠BAE。∴∠BAE=∠AEB.
∴AB=EB.∴四边形ABEF是菱形。∴BF平分∠ABC;
(2)∵四边形ABEF为菱形;∴BE=AB=6.∵四边形ABCD∽四边形CEFD,
∴,即。
解得BC=3±3(负值舍去),∴BC=3+3.
