第4章 相交线与平行线单元检测试卷(含解析)
文档属性
| 名称 | 第4章 相交线与平行线单元检测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 09:21:08 | ||
图片预览



文档简介
湘教版七年级第4章相交线与平行线单元检测试卷
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题4分,共48分)
1.如图,已知AB、CD、EF相交于点O,已知∠AOE=24°,则∠BOE为( )
A.24° B.124° C.156° D.不能确定
2.已知C,D,E三点在直线AB上,P为直线AB外一点,PC=1,PD=2,PE=3,则点P到直线AB的距离( )
A.小于1 B.不小于1 C.大于1 D.不大于1
3.如图,△ABC沿着BC方向平移3cm得到△DEF,已知BC=5cm,那么EC的长为( )cm.
A.2 B.4 C.6 D.8
4.如图,若∠1=∠2,∠3=48°22',则∠4的度数为(?? )
A.131°38' B.129°22' C.128°38' D.125°22'
5.如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )
A.44° B.45° C.46° D.56°
6.平面内有三条直线,那么它们的交点个数有( )
A.0个或1个 B.0个或2个 C.0个或1个或2个 D.0个或1个或2个或3个
7.下列选项中∠1与∠2不是同位角的是( )
A. B. C. D.
8.在同一平面内,互不重合的三条直线公共点的个数是( )
A.只可能是0个、1个或3个
B.只可能是0个、1个或2个
C.只可能是0个、2个或3个
D.0个、1个、2个或3个都有可能
9.如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )
A.变大 B.变小 C.不变 D.无法确定
11.如图所示,能表示直线AB、CD之间距离的是线段( )
A.PQ的长度 B.PM的长度 C.PN的长度 D.以上都不对
12.下列说法:
①若a与c相交,b与c相交,则a与b相交;②若a//b,b//c,那么a//c;③经过直线外一点有且只有一条直线与已知直线平行;④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A.3个 B.2个 C.1个 D.0个
二、填空题(6小题,每题4分,共24分)
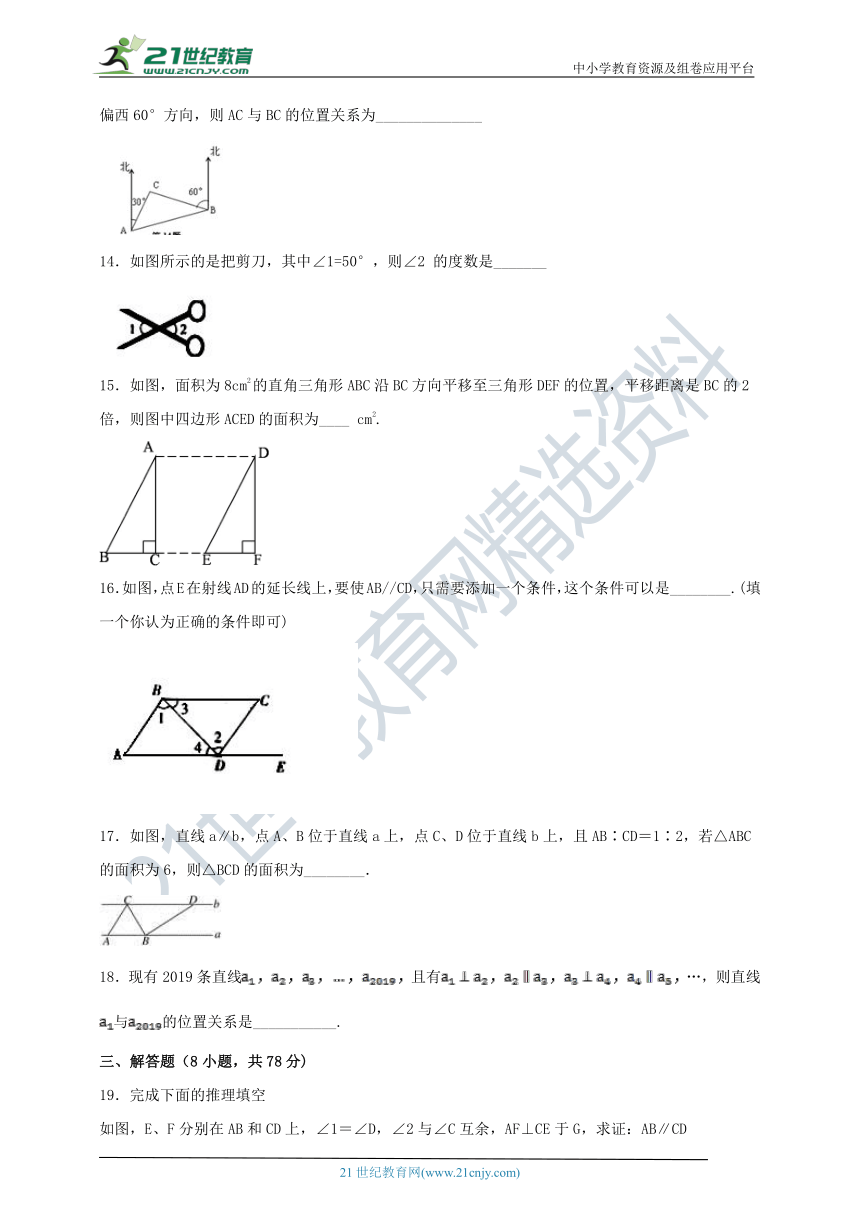
13.如图,A、B为观测站,C为岛屿,现在A处测得C在A北偏东30°方向,在B处测得C在B北偏西60°方向,则AC与BC的位置关系为______________
14.如图所示的是把剪刀,其中∠1=50°,则∠2 的度数是_______
15.如图,面积为8cm2的直角三角形ABC沿BC方向平移至三角形DEF的位置,平移距离是BC的2倍,则图中四边形ACED的面积为____ cm2.
16.如图,点E在射线AD的延长线上,要使AB//CD,只需要添加一个条件,这个条件可以是________.(填一个你认为正确的条件即可)
17.如图,直线a∥b,点A、B位于直线a上,点C、D位于直线b上,且AB∶CD=1∶2,若△ABC的面积为6,则△BCD的面积为________.
18.现有2019条直线且有…,则直线与的位置关系是___________.
三、解答题(8小题,共78分)
19.完成下面的推理填空
如图,E、F分别在AB和CD上,∠1=∠D,∠2与∠C互余,AF⊥CE于G,求证:AB∥CD
证明:∵AF⊥CE ∴∠CGF=90°(垂直的定义)
∵∠1=∠D(已知)
∴________∥________( )
∴∠4=________=90° ( )
又∵∠2与∠C互余(已知),∠2+∠3+∠4=180°
∴∠2+∠C=∠2+________=90°
∴∠C=________
∴AB∥CD( )
20.如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠ADE=∠AED.试说明:DE∥FB.
21.如图,在ΔABC中,CD是高,点E、F、G分别在BC、AB、AC上且EF⊥AB,DG∥BC,试判断∠1与∠2的大小关系,并说明理由.
22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)直接写出图中∠AOC的对顶角:__________,∠EOB的邻补角:__________.
(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.
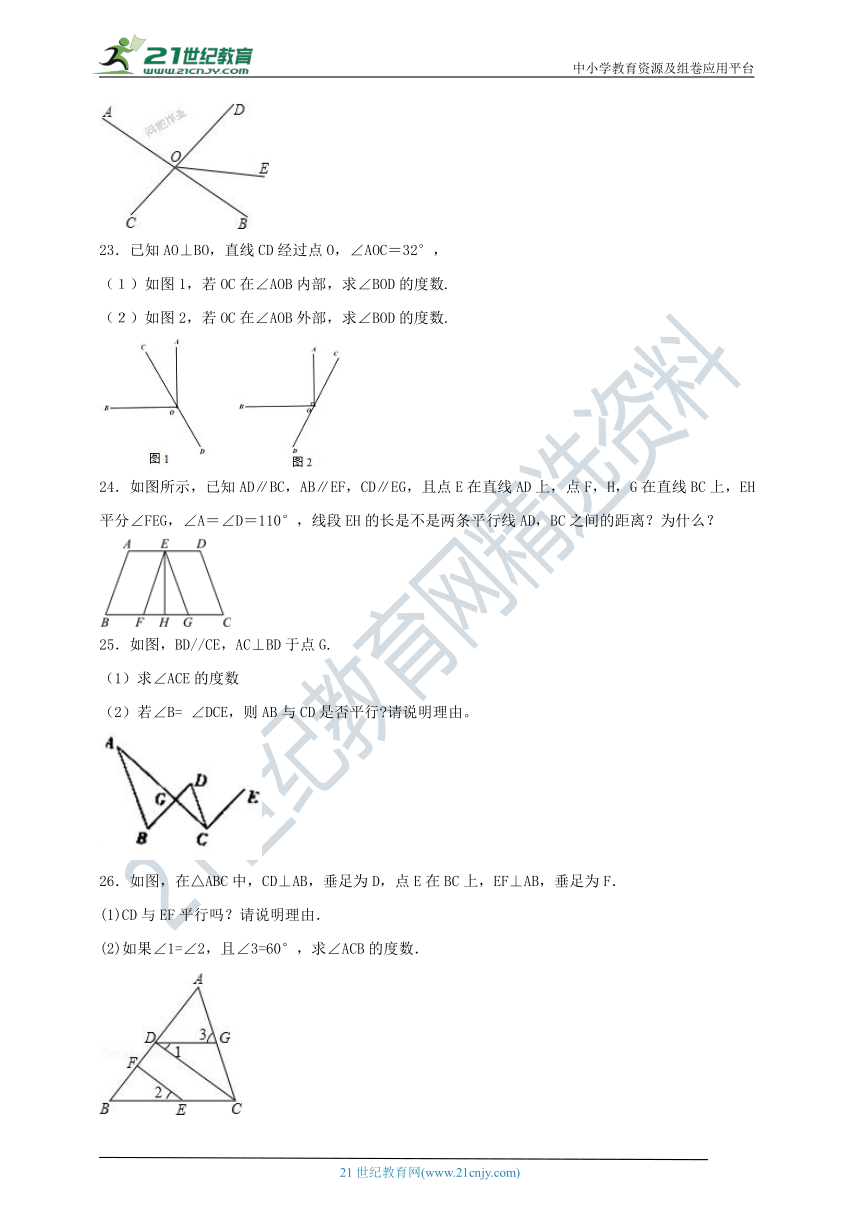
23.已知AO⊥BO,直线CD经过点O,∠AOC=32°,
(1)如图1,若OC在∠AOB内部,求∠BOD的度数.
(2)如图2,若OC在∠AOB外部,求∠BOD的度数.
24.如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
25.如图,BD//CE,AC⊥BD于点G.
(1)求∠ACE的度数
(2)若∠B= ∠DCE,则AB与CD是否平行?请说明理由。
26.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?请说明理由.
(2)如果∠1=∠2,且∠3=60°,求∠ACB的度数.
参考答案
1.【考点】邻补角的定义
【分析】根据∠AOE+∠BOE=180°求解即可.
解:∵AOE+∠BOE=180°,∠AOE=24°,
∴∠BOE=180°-24°=156°.
故选C.
【点睛】本题考查了邻补角的定义,如果两个角有一条公共边,其余两边互为反向延长线,那么这两个角互为邻补角,互为邻补角的两个角的和等于180°.
2.【考点】点到直线的距离,垂线段最短
【分析】根据点到直线的距离,垂线段最短即可判定.
解:设点P到直线的距离为l. ∵直线外一点到直线的距离,垂线段最短, ∴①当点P到直线的距离l与PC=1,PD=2,PE=3中的任何一条都不重合时,l<1; ②当点P到直线的距离l与,PC=1,PD=2,PE=3中的一条重合时,即与其中距离最短的PC重合时,l=PC=1. 综合①②l≤1,即l不大于1. 故选:D.
【点睛】本题考查点到直线的距离的概念.解题的关键是牢固掌握“点到直线的距离,垂线段最短”.
3.【考点】平移的性质
【分析】根据平移的性质得BE=3cm,即可求出EC的长.
解:∵△ABC沿着BC方向平移3cm得到△DEF,
∴BE=3cm,
∴EC=5-3=2cm.
故选A.
【点睛】此题主要考查平移的性质,解题的关键是熟知平移的性质.
4.【考点】角的运算,平行线的判定与性质
【分析】根据平行线的判定与性质即可得解.
解:
解:如图,
∵∠1=∠2,
∴AB∥CD,
∴∠4=∠5=180°﹣∠3=180°﹣48°22'=131°38'.
故选A.
【点睛】本题主要考查角的运算,平行线的判定与性质,解此题的关键在于熟练掌握其知识点.
5.【考点】垂线的性质,平角的定义
【分析】由垂线的性质以及平角的定义即可求出答案.
解:∵OM⊥l1,
∴α+90°+β=180°,
∴α=46°,
故选:C.
【点睛】本题考查垂线的性质,属于基础题型.
6.【考点】相交线
【分析】直线的位置关系不明确,应分情况讨论.
解:当三条直线平行时,交点个数为0;
当三条直线相交于1点时,交点个数为1;
当三条直线中,有两条平行,另一条分别与他们相交时,交点个数为2;
当三条直线互相不平行时,交点个数为3;
所以,它们的交点个数有4种情形.
故选D.
【点睛】本题涉及直线相交的相关知识,难度中等.
7.【考点】同位角
【分析】根据同位角的特征:两条直线被第三条直线所截形成的角中,两个角都在两条被截直线的同侧,并且在第三条直线(截线)的同旁,由此判断即可.
解:A、B、D中∠1和∠2是同位角;C、∠1和∠2不满足两条直线被第三条直线所截形成的角,所以不是同位角;
故选:C.
【点睛】本题考查三线八角中的某两个角是不是同位角,同位角完全由两个角在图形中的相对位置决定.在复杂的图形中判别同位角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形.
8.【考点】直线的交点个数问题
【分析】分三条直线互相平行、有两条平行和三条直线都不平行三种情况讨论.
解:因为三条直线位置不明确,所以分情况讨论: ①三条直线互相平行,有0个交点; ②一条直线与两平行线相交,有2个交点; ③三条直线都不平行,有1个或3个交点; 所以交点个数可能是0、1、2、3. 故选:D.
【点睛】考查了直线的交点个数问题.此类题没有明确平面上三条不重合直线的相交情况,需要运用分类讨论思想,解答时要分各种情况解答,要考虑到可能出现的所有情形,不要遗漏,否则讨论的结果就不全面.
9.【考点】平行线的性质和判定,角平分线定义
【分析】根据平行线的性质求出∠ACB=∠E,根据角平分线定义和平行线的性质求出∠ABF=∠CBF=∠ADC=∠EDC,推出BF∥DC,再根据平行线的性质判断即可.
解:∵BC∥DE,
∴∠ACB=∠E,∴①正确;
∵BC∥DE,
∴∠ABC=∠ADE,
∵BF平分∠ABC,DC平分∠ADE,
∴∠ABF=∠CBF=∠ABC,∠ADC=∠EDC=∠ADE,
∴∠ABF=∠CBF=∠ADC=∠EDC,
∴BF∥DC,
∴∠BFD=∠FDC,
∴根据已知不能推出∠ADF=∠CDF,∴②错误;③错误;
∵∠ABF=∠ADC,∠ADC=∠EDC,
∴∠ABF=∠EDC,
∵DE∥BC,
∴∠BCD=∠EDC,
∴∠ABF=∠BCD,∴④正确;
即正确的有2个,
故选C.
【点睛】本题考查了平行线的性质和判定,角平分线定义的应用,能灵活运用平行线的性质和判定进行推理是解此题的关键.
10.【考点】三角形的面积,平行线间的距离
【分析】先确定出点P到CD的距离是否变化,然后再依据三角形的面积公式进行判断即可.
解:∵直线AB∥CD,P是AB上的动点,
∴当点P的位置变化时,点P到CD的距离不变即△PCD的边CD上的高不变.
∴△PCD的面积不变.
故选C.
【点睛】本题主要考查的是三角形的面积、平行线间的距离,确定出三角形的高为不变量是解题的关键.
11.【考点】平行线之间的距离
【分析】根据两平行线之间的距离可以用垂线段表示,而相交的直线无法表示距离进行解答.
解:∵不能确定直线AB、CD的位置关系, ∴无法确定直线AB、CD之间距离, 故选:D.
【点睛】考查的是平行线之间的距离,从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.
12.【考点】平行公理及推论,相交线、平行线的定义
【分析】利用同一个平面内,两条直线的位置关系解答.
解:①若a与c相交,b与c相交,则a与b不一定相交;故错误;
②若a∥b,b∥c,那么a∥c;故正确;
③在同一平面内,过直线外一点有且只有一条直线与已知直线平行;故错误;
④在同一平面内,两条直线的位置关系有平行、相交两种;故错误.
故选C.
【点睛】本题考查了平行公理及推论,相交线、平行线的定义,熟记熟记公理、定理对学好几何比较关键.
13.【考点】平行线的性质
【分析】根据平行线的性质即可求出.
解:根据题意作CD∥北方向,
由两直线平行,内错角相等得出∠ACD=30°,∠BCD=60°,
故∠ACB=∠ACD+∠BCD=90°
则AC⊥BC.
【点睛】此题主要考查平行线的性质,解题的关键是熟知平行线的性质.
14.【考点】对顶角
【分析】根据对顶角的性质即可得.
解:观察图形可知∠1与∠2互为对顶角,
所以∠2=∠1=50°,
故答案为:50°.
【点睛】本题考查了对顶角,正确理解对顶角的性质是解题的关键.
15.【考点】平移的性质
【分析】根据平移的性质可以知道四边形ACED的面积是三个△ABC的面积,依此计算即可.
解:∵平移的距离是边BC长的两倍,
∴BC=CE=EF,
∴四边形ACED的面积是三个△ABC的面积;
∴四边形ACED的面积=8×3=24 cm2.
故答案为:24.
【点睛】考查平移的性质,根据平移的性质得到四边形ACED的面积是三个△ABC的面积是解题的关键.
16.【考点】平行线的判定
【分析】找到相等的同位角、内错角或互补的同旁内角即可.
解:若∠1=∠2,则AB∥CD;
若∠A=∠CDE,则AB∥CD;
若∠C+∠ABC= 180°,则AB∥CD,
故答案为:∠l=∠2或∠A=∠CDE 或∠C+∠ABC= 180°(答案不唯一).
【点睛】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.
17.【考点】平行线间的距离,三角形的面积
【分析】根据两平行线间的距离处处相等,结合三角形的面积公式,知△BCD和△ABC的面积比等于CD:AB,从而进行计算.
解:过C作CM⊥AB于M,过B作BN⊥CD于N,
∵a∥b,
∴CM=BN,
∴S△ABC=BA·CM,S△CDB=CD·BN,
∴S△ABC∶S△CDB=AB:CD=1∶2,
∵△ABC的面积为6,
∴△BCD的面积为12,
故答案为:12.
【点睛】本题考查了平行线间的距离以及三角形的面积比的一种方法,即等高的两个三角形的面积比等于它们的底的比.
18.【考点】平行公理,平行线的性质
【分析】根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答,进而得出规律:a1与其它直线的位置关系为每4个一循环,垂直、垂直、平行、平行,根据此规律即可判断.
解:先判断直线a1与a3的位置关系是:a1⊥a3.
理由如下:如图1,∵a1⊥a2,
∴∠1=90°,
∵a2∥a3,
∴∠2=∠1=90°,
∴a1⊥a3;
再判断直线a1与a4的位置关系是:a1∥a4,如图2;
∵直线a1与a3的位置关系是:a1⊥a3,
直线a1与a4的位置关系是:a1∥a4,
∵2019÷4=504…3,
∴直线a1与a2015的位置关系是:垂直.
故答案为:垂直.
【点睛】本题考查了平行公理的推导,作出图形更有利于规律的发现以及规律的推导,解题的关键是:结合图形先判断几组直线的关系,然后找出规律.
19.【考点】平行线的判定与性质、余角和补角
【分析】与垂直的定义得出∠CGF=90°,由平行线的判定证出AF∥DE,得出∠4=∠CGF=90°,再证出∠C=∠3,即可得出结论.
解:∵AF⊥CE, ∴∠CGF=90°(垂直的定义) ∵∠1=∠D(已知) ∴AF∥DE,(同位角相等,两直线平行) ∴∠4=∠CGF=90° (两直线平行,同位角相等), 又∵∠2与∠C互余(已知),∠2+∠3+∠4=180°, ∴∠2+∠C=∠2+∠3=90°, ∴∠C=∠3, ∴AB∥CD (内错角相等,两直线平行). 故答案为:AF,DE,同位角相等,两直线平行;∠CGF,两直线平行,同位角相等;∠3;∠3;内错角相等,两直线平行.
【点睛】本题考查了平行线的判定与性质、余角和补角;熟练掌握平行线的判定与性质是解决问题的关键.
20.【考点】平行线的判定,角平分线定义
【分析】根据角平分线定义及∠CDA=∠CBA可得∠ADE=∠ABF,利用等量代换可得∠AED=∠ABF,根据平行线判定定理即可得DE//FB.
解:∵DE平分∠CDA,BF平分∠CBA,
∴∠ADE=∠CDA,∠ABF=∠CBA,
∵∠CDA =∠CBA,
∴∠ADE=∠ABF,
∵∠ADE=∠AED,
∴∠AED=∠ABF,
∴DE∥FB.
【点睛】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.
21.【考点】平行线的判定与性质,垂直的定义
【分析】由DG∥BC,根据“两直线平行,内错角相等”得到∠1=∠DCE,由CD是高,EF⊥AB,得到∠CDB=∠EFB=90°,根据平行线的判定得到CD∥EF,由平行线的性质:两直线平行,同位角相等,得到∠DCE=∠2,即可得到∠1=∠2.
解:相等,理由如下:
∵CD是高,∴CD ⊥AB,∴∠CDB=90°
∵ EF⊥AB, ∴∠EFB=90°
∴∠CDB=∠EFB,∴EF∥CD
∴∠2= ∠DCB
∵ DG∥BC ∴∠1= ∠DCB
∴∠1=∠2
【点睛】本题考查了平行线的判定与性质以及垂直的定义,熟练掌握相关的定理和定义是解题的关键.
22.【考点】对顶角和邻补角的定义
【分析】(1)根据对顶角和邻补角的定义直接写出即可; (2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
解:(1)∠AOC的对顶角是∠BOD,∠EOB的邻补角是∠AOE, 故答案为:∠BOD,∠AOE; (2)∵∠AOC=70°, ∴∠BOD=∠AOC=70°, ∵∠BOE:∠EOD=2:3, ∴∠BOE= ×70°=28°, ∴∠AOE=180°-28°=152°. ∴∠AOE的度数为152°.
【点睛】本题主要考查了对顶角和邻补角的定义,利用对顶角相等的性质和互为邻补角的两个角的和等于180°求解是解答此题的关键.
23.【考点】垂线的定义,邻补角的定义,平角的定义
【分析】(1)先求出∠BOC的度数,然后根据邻补角的定义求∠BOD的度数;
(2)根据∠AOC+∠AOB+∠BOD=180°即可求∠BOD的度数.
解:(1)∵AO⊥BO,
∴∠AOB=90°.
∵∠AOC=32°,
∴∠BOC=90°-32°=58°,
∴∠BOD=180°-58°=122°;
(2)∵∠AOB=90°,∠AOC=32°,
∴∠BOD=180°-90°-32°=58°.
【点睛】本题考查了垂线的定义,邻补角的定义及平角的定义,熟练掌握相关定义是解答本题的关键.
24.【考点】行线间的距离,平行线的定义
【分析】根据平行条件证明∠AEF=∠DEG,再根据角平分线得∠FEH=∠GEH,相加即可得∠AEH=∠DEH=90°,从而证明EH⊥AD即可解题.
解:是.
理由:因为AB∥EF,
所以∠A=∠FED=110°.
因为CD∥EG,所以∠D=∠AEG=110°,
所以∠AEF=∠DEG.
因为EH平分∠FEG,
所以∠FEH=∠GEH,
所以∠FEH+∠AEF=∠GEH+∠DEG,
即∠AEH=∠DEH.
而∠AEH+∠DEH=180°,
所以∠AEH=∠DEH=90°,
所以EH⊥AD,
所以EH的长是两条平行线AD,BC之间的距离.
【点睛】本题考查了平行线间的距离,平行线的定义,属于简单题,熟悉性质并证明EH⊥AD是解题关键.
25.【考点】垂直的定义,平行线的性质与判定
【分析】(1)根据垂直的定义可得∠AGD=90°,再根据平行线的性质即可求得∠ACE的度数;
(2)由BD//CE可得∠D=∠DEC,继而由等量代换可得∠B=∠D,由此即可判断出AB//CD.
解:(1)因为AC⊥BD,
所以∠AGD=90°,
又因为BD//CE,
所以∠ACE=∠AGD=90°;
(2)AB//CD,理由如下:
因为BD//CE,
所以∠D=∠DEC,
因为∠B=∠DCE,
所以∠B=∠D,
所以AB//CD.
【点睛】本题考查了垂直的定义,平行线的性质与判定,熟练掌握平行线的性质与判定是解题的关键.
26.【考点】平行线的判定与性质
【分析】(1)根据垂直得出∠CDB=∠EFB=90°,根据平行线的判定得出即可; (2)根据平行线的性质得出∠2=∠BCD,求出∠1=∠BCD,根据平行线的判定得出DG∥BC,根据平行线的性质得出即可.
(1)证明:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴CD∥EF;
(2)∵CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC,
∴∠3=∠ACB=60°.
【点睛】考查平行线的判定与性质,掌握平行线的判定定理与性质定理是解题的关键.
班级_____________考号______________姓名_______________总分_________________
一、选择题(12小题,每题4分,共48分)
1.如图,已知AB、CD、EF相交于点O,已知∠AOE=24°,则∠BOE为( )
A.24° B.124° C.156° D.不能确定
2.已知C,D,E三点在直线AB上,P为直线AB外一点,PC=1,PD=2,PE=3,则点P到直线AB的距离( )
A.小于1 B.不小于1 C.大于1 D.不大于1
3.如图,△ABC沿着BC方向平移3cm得到△DEF,已知BC=5cm,那么EC的长为( )cm.
A.2 B.4 C.6 D.8
4.如图,若∠1=∠2,∠3=48°22',则∠4的度数为(?? )
A.131°38' B.129°22' C.128°38' D.125°22'
5.如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )
A.44° B.45° C.46° D.56°
6.平面内有三条直线,那么它们的交点个数有( )
A.0个或1个 B.0个或2个 C.0个或1个或2个 D.0个或1个或2个或3个
7.下列选项中∠1与∠2不是同位角的是( )
A. B. C. D.
8.在同一平面内,互不重合的三条直线公共点的个数是( )
A.只可能是0个、1个或3个
B.只可能是0个、1个或2个
C.只可能是0个、2个或3个
D.0个、1个、2个或3个都有可能
9.如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )
A.变大 B.变小 C.不变 D.无法确定
11.如图所示,能表示直线AB、CD之间距离的是线段( )
A.PQ的长度 B.PM的长度 C.PN的长度 D.以上都不对
12.下列说法:
①若a与c相交,b与c相交,则a与b相交;②若a//b,b//c,那么a//c;③经过直线外一点有且只有一条直线与已知直线平行;④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A.3个 B.2个 C.1个 D.0个
二、填空题(6小题,每题4分,共24分)
13.如图,A、B为观测站,C为岛屿,现在A处测得C在A北偏东30°方向,在B处测得C在B北偏西60°方向,则AC与BC的位置关系为______________
14.如图所示的是把剪刀,其中∠1=50°,则∠2 的度数是_______
15.如图,面积为8cm2的直角三角形ABC沿BC方向平移至三角形DEF的位置,平移距离是BC的2倍,则图中四边形ACED的面积为____ cm2.
16.如图,点E在射线AD的延长线上,要使AB//CD,只需要添加一个条件,这个条件可以是________.(填一个你认为正确的条件即可)
17.如图,直线a∥b,点A、B位于直线a上,点C、D位于直线b上,且AB∶CD=1∶2,若△ABC的面积为6,则△BCD的面积为________.
18.现有2019条直线且有…,则直线与的位置关系是___________.
三、解答题(8小题,共78分)
19.完成下面的推理填空
如图,E、F分别在AB和CD上,∠1=∠D,∠2与∠C互余,AF⊥CE于G,求证:AB∥CD
证明:∵AF⊥CE ∴∠CGF=90°(垂直的定义)
∵∠1=∠D(已知)
∴________∥________( )
∴∠4=________=90° ( )
又∵∠2与∠C互余(已知),∠2+∠3+∠4=180°
∴∠2+∠C=∠2+________=90°
∴∠C=________
∴AB∥CD( )
20.如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠ADE=∠AED.试说明:DE∥FB.
21.如图,在ΔABC中,CD是高,点E、F、G分别在BC、AB、AC上且EF⊥AB,DG∥BC,试判断∠1与∠2的大小关系,并说明理由.
22.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)直接写出图中∠AOC的对顶角:__________,∠EOB的邻补角:__________.
(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数.
23.已知AO⊥BO,直线CD经过点O,∠AOC=32°,
(1)如图1,若OC在∠AOB内部,求∠BOD的度数.
(2)如图2,若OC在∠AOB外部,求∠BOD的度数.
24.如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
25.如图,BD//CE,AC⊥BD于点G.
(1)求∠ACE的度数
(2)若∠B= ∠DCE,则AB与CD是否平行?请说明理由。
26.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?请说明理由.
(2)如果∠1=∠2,且∠3=60°,求∠ACB的度数.
参考答案
1.【考点】邻补角的定义
【分析】根据∠AOE+∠BOE=180°求解即可.
解:∵AOE+∠BOE=180°,∠AOE=24°,
∴∠BOE=180°-24°=156°.
故选C.
【点睛】本题考查了邻补角的定义,如果两个角有一条公共边,其余两边互为反向延长线,那么这两个角互为邻补角,互为邻补角的两个角的和等于180°.
2.【考点】点到直线的距离,垂线段最短
【分析】根据点到直线的距离,垂线段最短即可判定.
解:设点P到直线的距离为l. ∵直线外一点到直线的距离,垂线段最短, ∴①当点P到直线的距离l与PC=1,PD=2,PE=3中的任何一条都不重合时,l<1; ②当点P到直线的距离l与,PC=1,PD=2,PE=3中的一条重合时,即与其中距离最短的PC重合时,l=PC=1. 综合①②l≤1,即l不大于1. 故选:D.
【点睛】本题考查点到直线的距离的概念.解题的关键是牢固掌握“点到直线的距离,垂线段最短”.
3.【考点】平移的性质
【分析】根据平移的性质得BE=3cm,即可求出EC的长.
解:∵△ABC沿着BC方向平移3cm得到△DEF,
∴BE=3cm,
∴EC=5-3=2cm.
故选A.
【点睛】此题主要考查平移的性质,解题的关键是熟知平移的性质.
4.【考点】角的运算,平行线的判定与性质
【分析】根据平行线的判定与性质即可得解.
解:
解:如图,
∵∠1=∠2,
∴AB∥CD,
∴∠4=∠5=180°﹣∠3=180°﹣48°22'=131°38'.
故选A.
【点睛】本题主要考查角的运算,平行线的判定与性质,解此题的关键在于熟练掌握其知识点.
5.【考点】垂线的性质,平角的定义
【分析】由垂线的性质以及平角的定义即可求出答案.
解:∵OM⊥l1,
∴α+90°+β=180°,
∴α=46°,
故选:C.
【点睛】本题考查垂线的性质,属于基础题型.
6.【考点】相交线
【分析】直线的位置关系不明确,应分情况讨论.
解:当三条直线平行时,交点个数为0;
当三条直线相交于1点时,交点个数为1;
当三条直线中,有两条平行,另一条分别与他们相交时,交点个数为2;
当三条直线互相不平行时,交点个数为3;
所以,它们的交点个数有4种情形.
故选D.
【点睛】本题涉及直线相交的相关知识,难度中等.
7.【考点】同位角
【分析】根据同位角的特征:两条直线被第三条直线所截形成的角中,两个角都在两条被截直线的同侧,并且在第三条直线(截线)的同旁,由此判断即可.
解:A、B、D中∠1和∠2是同位角;C、∠1和∠2不满足两条直线被第三条直线所截形成的角,所以不是同位角;
故选:C.
【点睛】本题考查三线八角中的某两个角是不是同位角,同位角完全由两个角在图形中的相对位置决定.在复杂的图形中判别同位角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形.
8.【考点】直线的交点个数问题
【分析】分三条直线互相平行、有两条平行和三条直线都不平行三种情况讨论.
解:因为三条直线位置不明确,所以分情况讨论: ①三条直线互相平行,有0个交点; ②一条直线与两平行线相交,有2个交点; ③三条直线都不平行,有1个或3个交点; 所以交点个数可能是0、1、2、3. 故选:D.
【点睛】考查了直线的交点个数问题.此类题没有明确平面上三条不重合直线的相交情况,需要运用分类讨论思想,解答时要分各种情况解答,要考虑到可能出现的所有情形,不要遗漏,否则讨论的结果就不全面.
9.【考点】平行线的性质和判定,角平分线定义
【分析】根据平行线的性质求出∠ACB=∠E,根据角平分线定义和平行线的性质求出∠ABF=∠CBF=∠ADC=∠EDC,推出BF∥DC,再根据平行线的性质判断即可.
解:∵BC∥DE,
∴∠ACB=∠E,∴①正确;
∵BC∥DE,
∴∠ABC=∠ADE,
∵BF平分∠ABC,DC平分∠ADE,
∴∠ABF=∠CBF=∠ABC,∠ADC=∠EDC=∠ADE,
∴∠ABF=∠CBF=∠ADC=∠EDC,
∴BF∥DC,
∴∠BFD=∠FDC,
∴根据已知不能推出∠ADF=∠CDF,∴②错误;③错误;
∵∠ABF=∠ADC,∠ADC=∠EDC,
∴∠ABF=∠EDC,
∵DE∥BC,
∴∠BCD=∠EDC,
∴∠ABF=∠BCD,∴④正确;
即正确的有2个,
故选C.
【点睛】本题考查了平行线的性质和判定,角平分线定义的应用,能灵活运用平行线的性质和判定进行推理是解此题的关键.
10.【考点】三角形的面积,平行线间的距离
【分析】先确定出点P到CD的距离是否变化,然后再依据三角形的面积公式进行判断即可.
解:∵直线AB∥CD,P是AB上的动点,
∴当点P的位置变化时,点P到CD的距离不变即△PCD的边CD上的高不变.
∴△PCD的面积不变.
故选C.
【点睛】本题主要考查的是三角形的面积、平行线间的距离,确定出三角形的高为不变量是解题的关键.
11.【考点】平行线之间的距离
【分析】根据两平行线之间的距离可以用垂线段表示,而相交的直线无法表示距离进行解答.
解:∵不能确定直线AB、CD的位置关系, ∴无法确定直线AB、CD之间距离, 故选:D.
【点睛】考查的是平行线之间的距离,从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.
12.【考点】平行公理及推论,相交线、平行线的定义
【分析】利用同一个平面内,两条直线的位置关系解答.
解:①若a与c相交,b与c相交,则a与b不一定相交;故错误;
②若a∥b,b∥c,那么a∥c;故正确;
③在同一平面内,过直线外一点有且只有一条直线与已知直线平行;故错误;
④在同一平面内,两条直线的位置关系有平行、相交两种;故错误.
故选C.
【点睛】本题考查了平行公理及推论,相交线、平行线的定义,熟记熟记公理、定理对学好几何比较关键.
13.【考点】平行线的性质
【分析】根据平行线的性质即可求出.
解:根据题意作CD∥北方向,
由两直线平行,内错角相等得出∠ACD=30°,∠BCD=60°,
故∠ACB=∠ACD+∠BCD=90°
则AC⊥BC.
【点睛】此题主要考查平行线的性质,解题的关键是熟知平行线的性质.
14.【考点】对顶角
【分析】根据对顶角的性质即可得.
解:观察图形可知∠1与∠2互为对顶角,
所以∠2=∠1=50°,
故答案为:50°.
【点睛】本题考查了对顶角,正确理解对顶角的性质是解题的关键.
15.【考点】平移的性质
【分析】根据平移的性质可以知道四边形ACED的面积是三个△ABC的面积,依此计算即可.
解:∵平移的距离是边BC长的两倍,
∴BC=CE=EF,
∴四边形ACED的面积是三个△ABC的面积;
∴四边形ACED的面积=8×3=24 cm2.
故答案为:24.
【点睛】考查平移的性质,根据平移的性质得到四边形ACED的面积是三个△ABC的面积是解题的关键.
16.【考点】平行线的判定
【分析】找到相等的同位角、内错角或互补的同旁内角即可.
解:若∠1=∠2,则AB∥CD;
若∠A=∠CDE,则AB∥CD;
若∠C+∠ABC= 180°,则AB∥CD,
故答案为:∠l=∠2或∠A=∠CDE 或∠C+∠ABC= 180°(答案不唯一).
【点睛】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.
17.【考点】平行线间的距离,三角形的面积
【分析】根据两平行线间的距离处处相等,结合三角形的面积公式,知△BCD和△ABC的面积比等于CD:AB,从而进行计算.
解:过C作CM⊥AB于M,过B作BN⊥CD于N,
∵a∥b,
∴CM=BN,
∴S△ABC=BA·CM,S△CDB=CD·BN,
∴S△ABC∶S△CDB=AB:CD=1∶2,
∵△ABC的面积为6,
∴△BCD的面积为12,
故答案为:12.
【点睛】本题考查了平行线间的距离以及三角形的面积比的一种方法,即等高的两个三角形的面积比等于它们的底的比.
18.【考点】平行公理,平行线的性质
【分析】根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答,进而得出规律:a1与其它直线的位置关系为每4个一循环,垂直、垂直、平行、平行,根据此规律即可判断.
解:先判断直线a1与a3的位置关系是:a1⊥a3.
理由如下:如图1,∵a1⊥a2,
∴∠1=90°,
∵a2∥a3,
∴∠2=∠1=90°,
∴a1⊥a3;
再判断直线a1与a4的位置关系是:a1∥a4,如图2;
∵直线a1与a3的位置关系是:a1⊥a3,
直线a1与a4的位置关系是:a1∥a4,
∵2019÷4=504…3,
∴直线a1与a2015的位置关系是:垂直.
故答案为:垂直.
【点睛】本题考查了平行公理的推导,作出图形更有利于规律的发现以及规律的推导,解题的关键是:结合图形先判断几组直线的关系,然后找出规律.
19.【考点】平行线的判定与性质、余角和补角
【分析】与垂直的定义得出∠CGF=90°,由平行线的判定证出AF∥DE,得出∠4=∠CGF=90°,再证出∠C=∠3,即可得出结论.
解:∵AF⊥CE, ∴∠CGF=90°(垂直的定义) ∵∠1=∠D(已知) ∴AF∥DE,(同位角相等,两直线平行) ∴∠4=∠CGF=90° (两直线平行,同位角相等), 又∵∠2与∠C互余(已知),∠2+∠3+∠4=180°, ∴∠2+∠C=∠2+∠3=90°, ∴∠C=∠3, ∴AB∥CD (内错角相等,两直线平行). 故答案为:AF,DE,同位角相等,两直线平行;∠CGF,两直线平行,同位角相等;∠3;∠3;内错角相等,两直线平行.
【点睛】本题考查了平行线的判定与性质、余角和补角;熟练掌握平行线的判定与性质是解决问题的关键.
20.【考点】平行线的判定,角平分线定义
【分析】根据角平分线定义及∠CDA=∠CBA可得∠ADE=∠ABF,利用等量代换可得∠AED=∠ABF,根据平行线判定定理即可得DE//FB.
解:∵DE平分∠CDA,BF平分∠CBA,
∴∠ADE=∠CDA,∠ABF=∠CBA,
∵∠CDA =∠CBA,
∴∠ADE=∠ABF,
∵∠ADE=∠AED,
∴∠AED=∠ABF,
∴DE∥FB.
【点睛】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.
21.【考点】平行线的判定与性质,垂直的定义
【分析】由DG∥BC,根据“两直线平行,内错角相等”得到∠1=∠DCE,由CD是高,EF⊥AB,得到∠CDB=∠EFB=90°,根据平行线的判定得到CD∥EF,由平行线的性质:两直线平行,同位角相等,得到∠DCE=∠2,即可得到∠1=∠2.
解:相等,理由如下:
∵CD是高,∴CD ⊥AB,∴∠CDB=90°
∵ EF⊥AB, ∴∠EFB=90°
∴∠CDB=∠EFB,∴EF∥CD
∴∠2= ∠DCB
∵ DG∥BC ∴∠1= ∠DCB
∴∠1=∠2
【点睛】本题考查了平行线的判定与性质以及垂直的定义,熟练掌握相关的定理和定义是解题的关键.
22.【考点】对顶角和邻补角的定义
【分析】(1)根据对顶角和邻补角的定义直接写出即可; (2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
解:(1)∠AOC的对顶角是∠BOD,∠EOB的邻补角是∠AOE, 故答案为:∠BOD,∠AOE; (2)∵∠AOC=70°, ∴∠BOD=∠AOC=70°, ∵∠BOE:∠EOD=2:3, ∴∠BOE= ×70°=28°, ∴∠AOE=180°-28°=152°. ∴∠AOE的度数为152°.
【点睛】本题主要考查了对顶角和邻补角的定义,利用对顶角相等的性质和互为邻补角的两个角的和等于180°求解是解答此题的关键.
23.【考点】垂线的定义,邻补角的定义,平角的定义
【分析】(1)先求出∠BOC的度数,然后根据邻补角的定义求∠BOD的度数;
(2)根据∠AOC+∠AOB+∠BOD=180°即可求∠BOD的度数.
解:(1)∵AO⊥BO,
∴∠AOB=90°.
∵∠AOC=32°,
∴∠BOC=90°-32°=58°,
∴∠BOD=180°-58°=122°;
(2)∵∠AOB=90°,∠AOC=32°,
∴∠BOD=180°-90°-32°=58°.
【点睛】本题考查了垂线的定义,邻补角的定义及平角的定义,熟练掌握相关定义是解答本题的关键.
24.【考点】行线间的距离,平行线的定义
【分析】根据平行条件证明∠AEF=∠DEG,再根据角平分线得∠FEH=∠GEH,相加即可得∠AEH=∠DEH=90°,从而证明EH⊥AD即可解题.
解:是.
理由:因为AB∥EF,
所以∠A=∠FED=110°.
因为CD∥EG,所以∠D=∠AEG=110°,
所以∠AEF=∠DEG.
因为EH平分∠FEG,
所以∠FEH=∠GEH,
所以∠FEH+∠AEF=∠GEH+∠DEG,
即∠AEH=∠DEH.
而∠AEH+∠DEH=180°,
所以∠AEH=∠DEH=90°,
所以EH⊥AD,
所以EH的长是两条平行线AD,BC之间的距离.
【点睛】本题考查了平行线间的距离,平行线的定义,属于简单题,熟悉性质并证明EH⊥AD是解题关键.
25.【考点】垂直的定义,平行线的性质与判定
【分析】(1)根据垂直的定义可得∠AGD=90°,再根据平行线的性质即可求得∠ACE的度数;
(2)由BD//CE可得∠D=∠DEC,继而由等量代换可得∠B=∠D,由此即可判断出AB//CD.
解:(1)因为AC⊥BD,
所以∠AGD=90°,
又因为BD//CE,
所以∠ACE=∠AGD=90°;
(2)AB//CD,理由如下:
因为BD//CE,
所以∠D=∠DEC,
因为∠B=∠DCE,
所以∠B=∠D,
所以AB//CD.
【点睛】本题考查了垂直的定义,平行线的性质与判定,熟练掌握平行线的性质与判定是解题的关键.
26.【考点】平行线的判定与性质
【分析】(1)根据垂直得出∠CDB=∠EFB=90°,根据平行线的判定得出即可; (2)根据平行线的性质得出∠2=∠BCD,求出∠1=∠BCD,根据平行线的判定得出DG∥BC,根据平行线的性质得出即可.
(1)证明:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴CD∥EF;
(2)∵CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC,
∴∠3=∠ACB=60°.
【点睛】考查平行线的判定与性质,掌握平行线的判定定理与性质定理是解题的关键.
