第3章 图形与坐标单元检测试卷（含解析）

湘教版八年级第3章图形与坐标单元检测试卷
班级_____________考号______________姓名_______________总分_________________
一、选择题（12小题，每题3分，共36分)
1．小敏的家在学校正南150m，正东方向200m处，如果以学校位置为原点，以正北、正东为正方向，则小敏家用有序数对表示为(　　)
A．(－200，－150) B．(200,150) C．(200，－150) D．(－200,150)
2．我市为了促进全民健身，举办“健步走”活动，朝阳区活动场地位于奥林匹克公园(路线：森林公园－玲珑塔－国家体育场－水立方)．如图，体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(－1,0)，森林公园的坐标为(－2,2)，则终点水立方的坐标为(　　)
A．(－2，－4) B．(－1，－4) C．(－2,4) D．(－4，－1)
3．点P(－3，－2)与坐标原点、(－3，0)围成的三角形的面积为( )
A．2 B．3 C．4 D．6
4．在直角坐标系中，将点P(－3，2)向右平移4个单位长度，再向下平移6个单位长度后，得到的点位于( )
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．某同学的座位号为(2，4)那么该同学的位置是（ ）
A．第2排第4列 B．第4排第2列 C．第2列第4排 D．不好确定
6．点P(－|a|－1，b2＋2)一定在(　　)
A．第一象限 B．第二象限 C．第三象限 D．第四象限
7．下列语句中，说法错误的是(　　)
A．点(0,0)是坐标原点
B．对于坐标平面内的任一点，都有唯一的一对有序实数与它对应
C．点A(a，－b)在第二象限，则点B(－a，b)在第四象限
D．若点P的坐标为(a，b)，且a·b＝0，则点P一定在坐标原点
8．如图，若在象棋盘上建立直角坐标系xOy，使“帥”位于点(－1，－2)，“馬”位于点(2，－2)，则“炮”位于点(　　)
A．(－2，－1) B．(0,0) C．(1，－2) D．(－1,1)
9．若x轴上的点P到y轴的距离为3,则点P的坐标为（ ）
A．（3，0） B．（0，3） C．（3，0）或（－3，0） D．（0，3）或（0，－3）
10．在平面直角坐标系xOy中，对于点P(x，y)，我们把点(-y+1，x+1)叫做点P伴随点.已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，An，….若点A1的坐标为(2，4)，点A2017的坐标为? (? )
A．(-3，3) B．(-2，-2) C．(3，-1) D．(2，4)
11．点M（m+1，m+3）在x轴上，则点M坐标为（ ）．
A．（0，－4） B．（4，0） C．（－2，0） D．（0，－2）
12．如图，点A，B的坐标分别为(2，0)，(0，1)．若将线段AB平移至A1B1的位置，则a＋b的值为(　　)
A．2 B．3 C．4 D．5
二、填空题（6小题，每题3分，共18分)
13．已知点A(x－4，x＋2)在y轴上，则x的值等于________．
14．已知点P的坐标（2-a，3a+6），且点P到两坐标轴的距离相等，则点P的坐标是_______________.
15．若点P（a,-b）在第二象限,则点Q（-ab,a+b）在第_______象限.
16．七年级（2）班教室里的座位共有7排8列，其中小明的座位在第3排第7列，简记为（3，7），小华坐在第5排第2列，则小华的座位可记作__________.
17．如下图,小强告诉小华图中A、B两点的坐标分别为（－3,5）,（3,5）,小华一下就说出了C在同一坐标系下的坐标________.
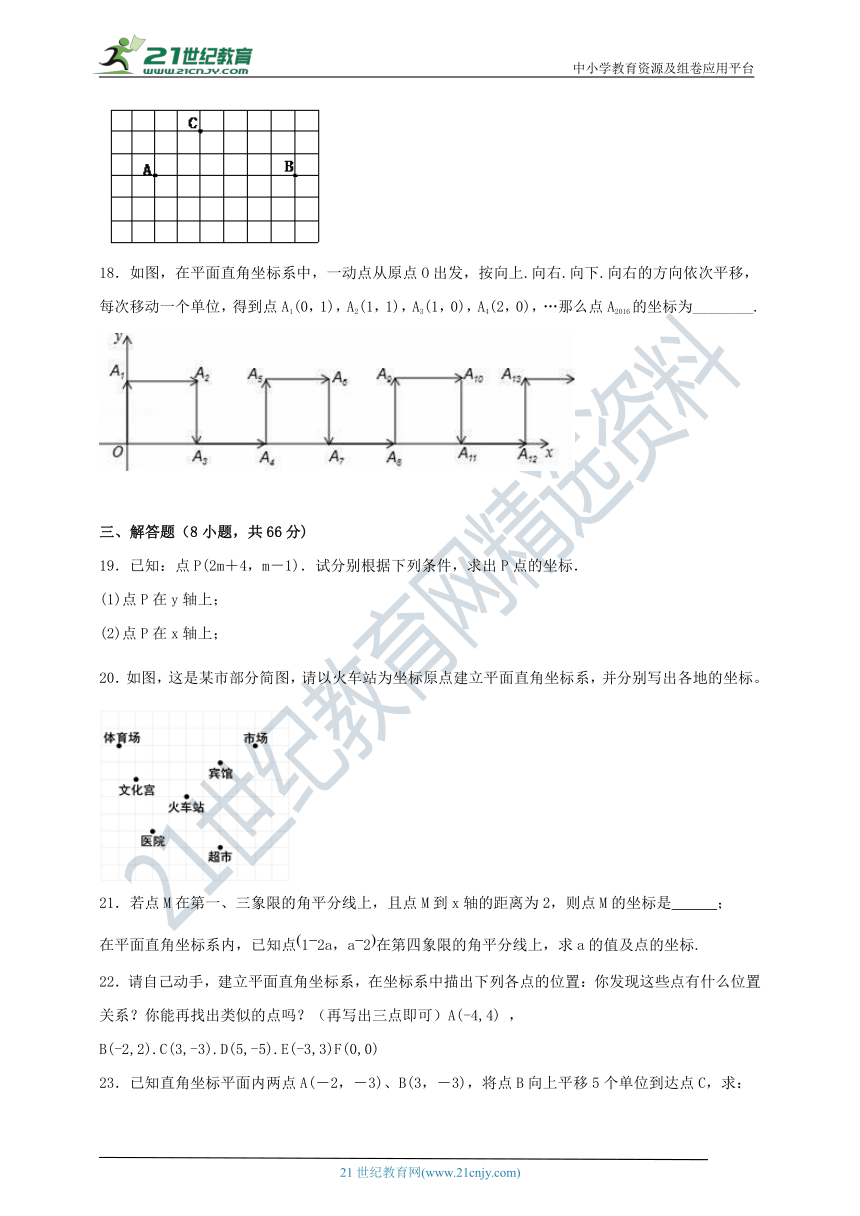
18．如图，在平面直角坐标系中，一动点从原点O出发，按向上.向右.向下.向右的方向依次平移，每次移动一个单位，得到点A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，…那么点A2016的坐标为________.
三、解答题（8小题，共66分)
19．已知：点P(2m＋4，m－1)．试分别根据下列条件，求出P点的坐标．
(1)点P在y轴上；
(2)点P在x轴上；
20．如图，这是某市部分简图，请以火车站为坐标原点建立平面直角坐标系，并分别写出各地的坐标。
21．若点M在第一、三象限的角平分线上，且点M到x轴的距离为2，则点M的坐标是 ；
在平面直角坐标系内，已知点(1(2a，a(2(在第四象限的角平分线上，求a的值及点的坐标.
22．请自己动手，建立平面直角坐标系，在坐标系中描出下列各点的位置：你发现这些点有什么位置关系？你能再找出类似的点吗？（再写出三点即可）A(-4,4) ，B(-2,2).C(3,-3).D(5,-5).E(-3,3)F(0,0)
23．已知直角坐标平面内两点A(－2，－3)、B(3，－3)，将点B向上平移5个单位到达点C，求：
(1)A、B两点间的距离；
(2)写出点C的坐标；
(3)四边形OABC的面积．
24．如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,
(1)请画出平移后的图形△A′B′C′
(2)并写出△A′B′C′各顶点的坐标.
(3)求出△A′B′C′的面积.
25．在如图所示的平面直角坐标系中表示下面各点A(0,3)，B(1，－3)，C(3，－5)，D(－3，－5)，E(3,5)，F(5,6)，G(5,0)根据描点回答问题：
(1)A点到原点的距离是________．
(2)将点C向x轴的负方向平移6个单位，它与点______重合．
(3)连接CE，则直线CE与坐标轴是什么关系？
(4)在以上七个点中，任意两点所形成的直线中，直接写出互相垂直的直线．
26．如图所示，形如字母“M”的图形上有五个点A(－3,3)，B(－3,1)，C(－2,2)，D(－1,3)，E(－1,1)，按要求分别作出其变化后的图形．
(1)横坐标不变，纵坐标乘－1；
(2)纵坐标不变，横坐标乘－1；
(3)横、纵坐标都乘－1.
观察(1)(2)(3)中要求作出的图形，这些图形与原图形有何联系？
参考答案
1．【考点】坐标确定位置
【分析】根据题意可以用相应的有序数对表示出小敏家的位置．
解：∵小敏的家在学校正南150m，正东方向200m处，如果以学校位置为原点，以正北、正东为正方向，
∴小敏家用有序数对表示为（200，-150），
故选C．
【点睛】本题考查坐标确定位置，解答本题的关键是明确题意，用相应的有序数对表示出小敏家的位置．
2．【考点】直角坐标系的建
【分析】根据题意作出直角坐标系，即可解出.
解：如图：水立方的坐标为(－2，－4)．
故选A
【点睛】此题主要考查直角坐标系的建立，解题的关键是根据题意建系.
3．【考点】直角坐标系的应用
【分析】依题意作出直角坐标系，即可求出围成的三角形的面积
解：由题意可得，如下图所示，
所以点P(－3，－2)与坐标原点、(－3,0)围成的三角形的面积是：×3×2＝3.
【点睛】此题主要考查直角坐标系的应用，解题的关键是根据坐标点作出直角坐标系.
4．【考点】坐标的平移
【分析】先将点P(－3,2)按题目要求平移得到新的坐标为(1，－4)，则在第四象限．
解：因为点P(－3,2)，所以向右平移4个单位长度，再向下平移6个单位长度后可得(－3＋4,2－6)，即(1，－4)，(1，－4)点在第四象限．
【点睛】此题主要考查坐标的平移，解题的关键是熟知各象限坐标的特点.
5．【考点】有序数对
【分析】1、分析题意，回忆用坐标确定位置的方法；
2、观察发现题中没有规定排和列的前后顺序；
3、接下来根据有序实数对的知识，解答本题.
解：题中没有规定排在前，列在后；还是列在前，排在后，
因此无法确定该同学的所坐位置.
故选D.
【点睛】在使用有序数对前，一定要先对有序数进行定义，否则很可能导致前后数表示的意义不明确，从而确定不出位置.例如本题没有规定有序数对的列和排谁在前，所以无法得知其所表示的含义.
6．【考点】点的坐标
【分析】先判断出点P的横坐标为负数，纵坐标为正数，然后根据各象限内点的坐标特征求解即可．
解：∵|a|＞0，
∴-|a|-1＜0，
∵b2＞0，
∴b2+2＞0．
∴点P的横坐标是负数，纵坐标是正数，
∴点P在第二象限．
故选B．
【点睛】本题考查了点的坐标，解答本题的关键在于记住各象限内点的坐标的符号，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
7．【考点】各象限内点的坐标的符号特征
【分析】根据各象限内点的坐标特征、有序实数对与平面的关系，解答即可．
解：A、点（0，0）是坐标原点，正确，故不符合题意；
B、对于坐标平面内的任一点，都有唯一的一对有序实数与它对应，正确，故不符合题意；
C、点A(a，-b)在第二象限，得a＜0，-b＞0，则-a＞0，b＜0，点B(-a，b)在第四象限，故不符合题意；
D、若点P的坐标为(a，b)，且a?b=0，则点P一定在坐标轴上，故D符合题意；
故选D．
【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
8．【考点】平面坐标系的建立
【分析】先根据“帥”的位置确定原点的坐标，建立平面直角坐标系，从而可以确定“炮”的位置．
解：根据条件建立平面直角坐标系：
由图得“炮”的坐标为：（0，0）．
故选B.
【点睛】本题考查了平面坐标系的建立，在平面直角坐标系中确定点的位置，本题难度较小．
9．【考点】点的坐标
【分析】1、回忆直角坐标系中点的坐标所代表的意义；
2、结合点的坐标的几何意义，根据题意可得点P纵坐标为0，且横坐标的绝对值为3；
3、再根据绝对值的性质即可得到点P的横坐标，从而可得到点P的坐标．
解：∵x轴上点P到y轴的距离为3，
∴点P纵坐标为0，且横坐标的绝对值为3，
∴点P坐标为（3，0）或（-3，0）．
故选C．
【点睛】本题主要考查了点的坐标的几何意义，横坐标的绝对值就是点到y轴的距离，纵坐标的绝对值就是点到x轴的距离．本题就是根据点P到y轴的距离为3得到点P的横坐标的绝对值是3，从而得到点P的横坐标，即可解答本题.
10．【考点】点的坐标规律
【分析】根据“伴随点”的定义依次求出各点，不难发现，每4个点为一个循环组依次循环，用2017除以4，根据商和余数的情况确定点A2017的坐标即可．
解：∵点A1的坐标为（2，4），∴A2（-4+1，2+1）即（-3，3），A3（-3+1，-3+1）即（-2，-2），A4（2+1，-2+1）即（3，-1），A5（2，4），…，依此类推，每4个点为一个循环组依次循环，∵2017÷4=504余1，∴点A2017的坐标与A1的坐标相同，为（2，4）；故选D．
【点睛】本题考查了点的坐标规律，读懂题目信息，理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键．
11．【考点】坐标轴上点的坐标特征
【分析】1、回想一下x轴上点的坐标特征；
2、根据x轴上的点的纵坐标为0可得m+3=0；
3、接下来解出m的值，点M的坐标也就容易得到了．
解：根据x轴上点的坐标特征可得m+3=0，
解得m=-3，则m+1=-2
故点M的坐标为（-2，0）
故选C.
【点睛】本题主要考查了坐标轴上点的坐标特征.x轴上的点，纵坐标为0；y轴上的点，横坐标为0.如此题就是根据点M在x轴上得到m+3=0，从而得到m的值，使问题得解的.
12．【考点】坐标系中点、线段的平移规律
【分析】直接利用平移中点的变化规律求解即可．
解：由B点平移前后的纵坐标分别为1、2，可得B点向上平移了1个单位，
由A点平移前后的横坐标分别是为2、3，可得A点向右平移了1个单位，
由此得线段AB的平移的过程是：向上平移1个单位，再向右平移1个单位，
所以点A、B均按此规律平移，
由此可得a=0+1=1，b=0+1=1，
故选：A．
【点睛】本题考查了坐标系中点、线段的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．
13．【考点】坐标轴上的点的坐标特点
【分析】根据y轴上的坐标横坐标为0即可求出.
解：因为点A(x－4，x＋2)在y轴上，所以x－4＝0，解得x＝4.
【点睛】此题主要考查坐标轴上的点，解题的关键是熟知坐标轴上的点的坐标特点.
14．【考点】点到两坐标轴的距离
【分析】点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数，就可以得到方程求出a的值，从而求出点的坐标．
解：∵点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数，∴分以下两种情考虑：①横纵坐标相等时，即当2-a=3a+6时，解得a=-1，∴点P的坐标是（3，3）；②横纵坐标互为相反数时，即当（2-a）+（3a+6）=0时，解得a=-4，∴点P的坐标是（6，-6）．
故答案填（3，3）或（6，-6）．
【点睛】因为这个点到两坐标轴的距离相等，即到坐标轴形成的角的两边距离相等，所以这个点一定在各象限的角平分线上．
15．【考点】平面直角坐标系中象限的点的坐标的符号特点
【分析】应先判断出所求的点的横纵坐标的符号，进而判断其所在的象限．
解：∵点P（a，-b）在第二象限，∴a＜0，b＜0，∴-ab＜0，a+b＜0，∴点Q（-ab，a+b）在第三象限．
故填：三．
【点睛】本题主要考查了平面直角坐标系中第二象限的点的坐标的符号特点．牢记四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
16．【考点】点的坐标
【分析】由已知条件知：横坐标表示第几排，纵坐标表示第几列．
解：由题意可知座位的表示方法为排在前，列在后，得小华的座位可记作（5，2）．
故答案填：（5，2）．
【点睛】本题是数学在生活中应用，平面位置对应平面直角坐标系，空间位置对应空间直角坐标系．可以做到在生活中理解数学的意义．
17．【考点】坐标的平移
【分析】根据已知两点坐标确定坐标系，然后确定其它点的位置．
解：由A，B两点的坐标分别为（-3，5），（3，5），可知，坐标原点不在图中出现，是以线段AB的中垂线为y轴，且向上为正方向，最下的水平线的纵坐标是2，以水平线为x轴，且向右为正方向，∴C点的坐标为（-1，7）．
【点睛】解题的关键是确定坐标原点和x，y轴的位置及方向，或者直接利用坐标系中的移动法则右加左减，上加下减来确定坐标．
18．【考点】坐标与图形变化-平移
【分析】观察不难发现，每四个点为一个循环组依次循环，前两个点的纵坐标都是1，第二、三个点的横坐标相同，第三、四个点都在x轴上，每一个循环组向右2个单位，用2016除以4，然后根据商和余数的情况确定即可．
解：由图可知，4个点为一个循环组依次循环，∵2016÷4=504，∴点A2016是第504循环组的最后一个点，504×2=1008，∴点A2016的坐标为（1008，0）．故答案为：（1008，0）．
【点睛】本题考查了坐标与图形变化-平移，仔细观察图形，发现每四个点为一个循环组依次循环是解题的关键．
19．【考点】点分坐标
【分析】(1)让横坐标为0求得m的值，代入点P的坐标即可求解；
(2)让纵坐标为0求得m的值，代入点P的坐标即可求解．
解：(1)令2m＋4＝0，解得m＝－2，所以P点的坐标为(0，－3)；
(2)令m－1＝0，解得m＝1，所以P点的坐标为(6,0)．
【点睛】此题主要考查直角坐标系的点，解题的关键是熟知坐标轴上的点的特点.
20．【考点】确定点的位置
【分析】确定原点位置，建立直角坐标系，根据坐标系表示各地的坐标．
解：如图所示：
火车站（0，0），医院（– 2，– 2），文化宫
（– 3，1），体育场（– 4，3），宾馆（2，2）
市场（4，3），超市（2，– 3）
【点睛】主要考查了建立直角坐标系确定点的位置，确定原点是解题的关键.
21．【考点】在一、三象限和二、四象限角平分线上的点的坐标特征
【分析】根据第一、三象限角平分线上点的坐标的特征是：横坐标与纵坐标相等，进而求出即可．在二、四象限角平分线上的点的横坐标和纵坐标互为相反数,可求出a的值和点的坐标．
解：（1）若点M在第一、三象限的角平分线上，且点M到x轴的距离为2，则点M的坐标是(2,2)或((2,(2)；
（2）若点(1(2a，a(2(在第四象限的角平分线上，
则1(2a+a(2=0，a=-1,
所以，点的坐标为(3，(3(．
故答案为：(2,2)或((2,(2)；a= (1，点的坐标为(3，(3(．
【点睛】此题主要考查了在一、三象限和二、四象限角平分线上的点的横纵坐标之间的关系．
22．【考点】点的坐标性质
【分析】根据各点的横纵坐标符号得出变化规律即可.
解：
这些点在同一直线上，在二四象限的角平分线上，举例:（1,-1），（7，-7），（-5,5）.
【点睛】此题主要考查了点的坐标性质,根据各点的坐标得出变与不变是解题关键.
23．【考点】直角坐标系的点
【分析】(1)A、B两点的横坐标差的绝对值即为A、B两点间的距离；
(2)将点B的横坐标不变，纵坐标加5即可求出点C的坐标；
(3)四边形OABC的面积等于三角形ODC面积与梯形OABD的面积之和.
解：(1)因为点A(－2，－3)、点B(3，－3)，所以AB＝3－(－2)＝5；
(2)因为点B(3，－3)，将点B向上平移5个单位到达点C，所以点C的坐标为(3,2)；
(3)如图，
设BC与x轴交于点D，
则S四边形OABC＝S三角形ODC＋S梯形OABD＝×3×2＋(3＋5)×3＝3＋12＝15.
【点睛】此题主要考查直角坐标系的点，解题的关键是熟知坐标点的定义与性质.
24．【考点】作图与平移变换
【分析】（1）根据图形平移的性质画出△A′B′C′即可；
（2）根据各点在坐标系的位置写出各点坐标即可；
（3）利用矩形的面积减去三个顶点三角形的面积即可.
解：（1）如图，△A′B′C′即为所求；
（2）由图可知A′(4,0)B′(1,3)C′(2,-2)；
（3）S△A′B′C′=.
【点睛】此题主要考查作图与平移变换，解题的关键是熟知坐标系的特点.
25．【考点】点的坐标性质以及平移的性质
【分析】(1)根据A点坐标可得出A点在y轴上，即可得出A点到原点的距离；
(2)根据点的平移的性质得出平移后的位置；
(3)利用图形性质得出直线CE与坐标轴的位置关系；
(4)利用图形性质得出互相垂直的直线．
解：由题意得，如图所示：
(1)A点到原点的距离是3.
(2)将点C向x轴的负方向平移6个单位，它与点D重合．
(3)直线CE与y轴平行，与x轴垂直；
(4)直线CD与CE垂直，直线CD与FG垂直．
故答案为：(1)3；(2)D；(3)垂直；(4)直线CD与CE垂直，直线CD与FG垂直．
【点睛】此题主要考查了点的坐标性质以及平移的性质，根据坐标系得出各点的位置是解题关键．
26．【考点】坐标与图形的性质
【分析】（1）根据题意求得A1(－3，－3)，B1(－3，－1)，C1(－2，－2)，D1(－1，－3)，E1(－1，－1)，顺次连结则得到所求作图形；（2）同（1）的方法求解即可；（3）同（1）的方法求解即可；观察所画的图形，比较即可解答.
解：(1)A、B、C、D、E五点的横坐标不变，纵坐标乘以－1，则得到A1(－3，－3)，B1(－3，－1)，C1(－2，－2)，D1(－1，－3)，E1(－1，－1)，顺次连结则得到所求作图形，如图B1A1C1D1E1．同理可得出(2)、(3)，如图E2D2C2A2B2、E3D3C3A3B3．
按(1)、(2)、(3)要求作出的图形形状和大小与原图形是完全一样的，其中把原图形沿x轴翻折可得图形(1)，沿y轴翻折可得图形(2)，绕O点旋转180°可得图形(3)．
【点睛】本题考查了坐标与图形的性质，点的坐标的变化引起图形的变化，图形的变化则带动图形上所有点的变化，画变化后的图形的关键是找出一些关键的点．