六年级下册数学优秀课件-6.3《整理与复习式与方程》人教新课标(2014秋) (共22张PPT)
文档属性
| 名称 | 六年级下册数学优秀课件-6.3《整理与复习式与方程》人教新课标(2014秋) (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 00:00:00 | ||
图片预览






文档简介
整理和复习
逸夫小学 曹会静
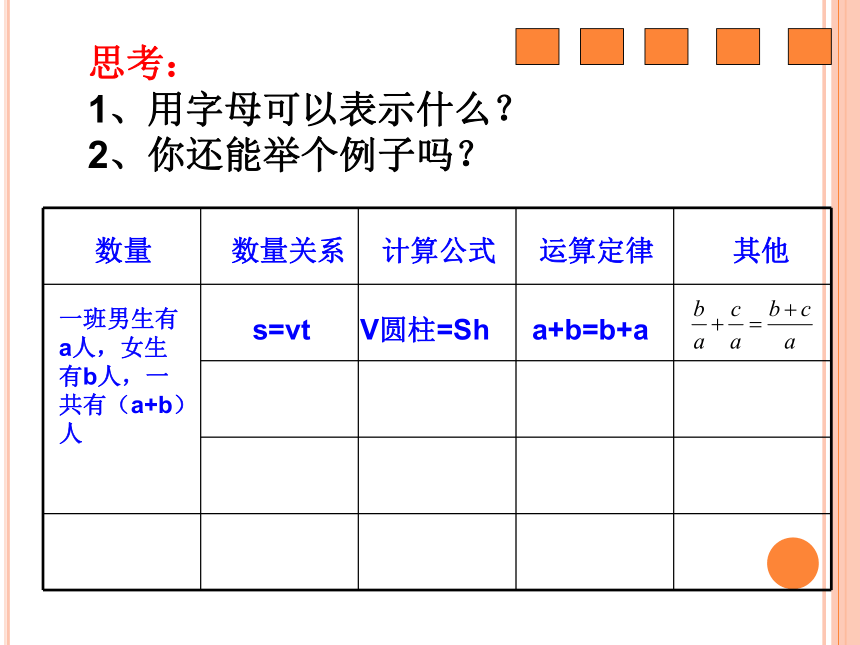
思考:
1、用字母可以表示什么?
2、你还能举个例子吗?
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人
s=vt
V圆柱=Sh
a+b=b+a
用字母可以表示具体的数量
1、小明今年a岁,妈妈比她大b岁,妈妈今年( )岁。
2、m表示一个偶数,与它相邻的两个偶数是( )和( )。
3、水果店有b千克苹果,一共要装6箱,平均每箱装( )千克。
4、一只青蛙每天吃a只害虫,100天吃( )只害虫。
a+b
m—2
m+2
b÷6
100a
思考:
1、含有字母的式子中简写的规则?
2、在省略乘号时要注意什么?
1、数字和字母相乘以及字母和字母相乘可以省略乘号,
或者写成“·”。
2、注意点:
a、省略乘号时,数字要写在字母的前面。
1可以省略不写。
例如:a×4=4a,b×1=b
b、两个a相乘可以写出a的平方。a×a=a?。
用字母表示数可以简明地表达数量关系
例如:
用s表示路程,v表示速度,t表示时间,那么
s=vt
c=at
如果工作总量用字母c表示,工作时间用t表示,工作效率用a表示,那么
用字母表示正比例关系:
用字母表示反比例关系:
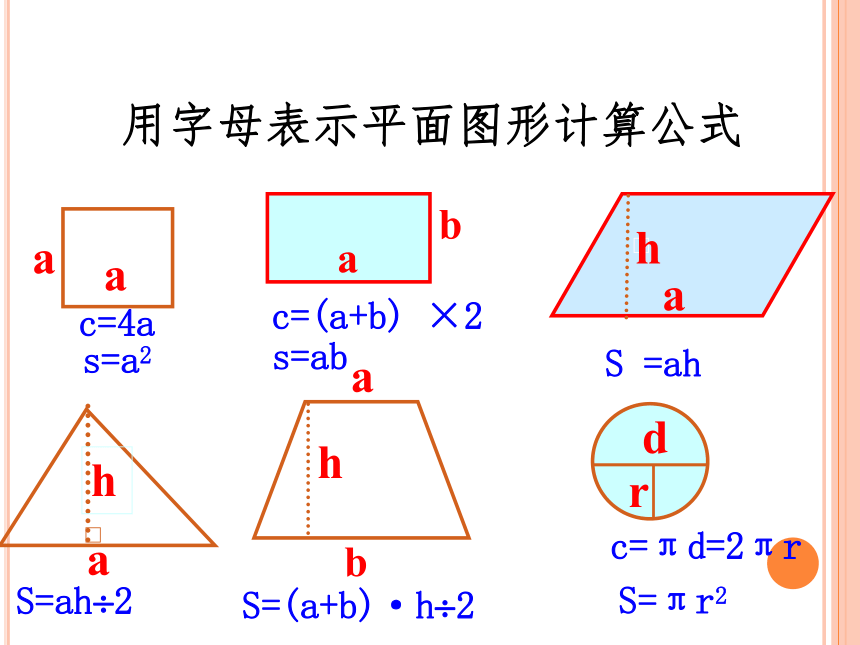
用字母表示平面图形计算公式
a
a
a
a
b
a
h
d
r
a
b
h
a
h
s
s
h
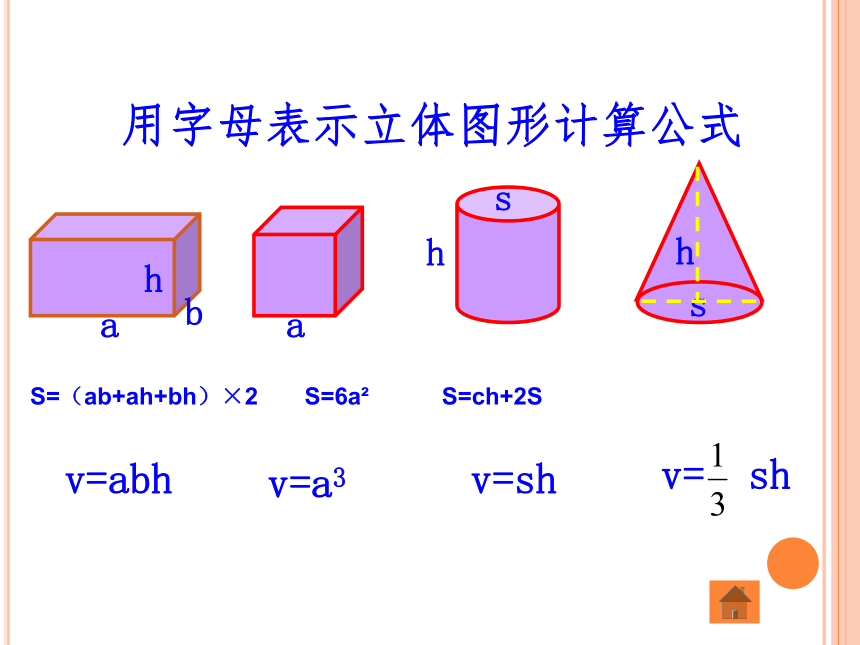
用字母表示立体图形计算公式
S=(ab+ah+bh)×2 S=6a? S=ch+2S
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
用字母表示运算定律和性质
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷ (b×c)
计算方法
cm、kg、m?……
计量单位
ABB ABB ABB……
一种规律
除法与分数的关系
因倍数
三、巩固练习
1. 连线。
比a多3的数
比a少3的数
3个a相加的和
a的3倍
a?
3a
a+3
a-3
3个a相乘的积
1.9+7=8.9 3x+6>9 x-1.5=1
x+ <12 x+20%x=3.6 2x+5.6=9.4
② ③
④ ⑤ ⑥
判断哪些是方程
请你回顾一下以下知识:
1、什么是方程?方程与等式有什么联系和区别?
2、等式的性质是什么?
3、什么是解方程?什么是方程的解?他们有什么区别?
4、解方程的依据是什么?
x-1.5=1
x+20%x=3.6 2x+5.6=9.4
1、什么是方程?方程与等式有什么关系?
含有未知数的等式叫方程。
方程一定是等式,但等式不一定是方程。
等式的性质:
1、等式两边同时加上或减去同一个数,左右两边仍然相等。
2、等式两边同时乘或除以同一个数(0除外),左右两边仍然相等。
2、什么是方程的解?什么是解方程?他们有什么区别?
方程的解:使方程左右两边相等的未知数的值。
解方程:求方程的解的过程。
一个具体的数
一个过程
3、解方程的依据是什么?
等式的性质
解方程 2x+5.6=9.4
解:
2x+5.6-5.6=9.4-5.6
2x=3.8
2x÷2=3.8÷2
x=1.9
(1)解方程过程中要注意什么?
(2)如何判断x=1.9是否是方程的解?
列方程解决问题。
小平在踢毽子比赛中踢了42下,她踢毽的数量是小云的 。小云踢了多少下?
1、用方程解决问题的基本步骤是什么?
2、其中最关键的是哪一步?
一般分5步:
1)根据题意,解设未知数为x。
2)找出具体的数量,列出等量关系式。
3)根据等量关系式,列出方程。
4)解方程
5)检验并答句。
思考:
1、用方程解决问题的基本步骤是什么?
2、其中最关键的是哪一步?
建议:
1.单位“1”未知时,用方程解决比较简便。
类型一:和倍、差倍的应用题,单位“1”未知用方程解决。
类型二:比谁的几倍多(少)几,单位“1”未知用方程解决。
类型三:甲数比乙数多(少)几分之几或百分之几。单位“1”乙数未知时用方程解决。
2.行程中的相遇问题、相距问题时,求相遇时间或一个车的速度时 ,用方程。
3.题目中数量关系比较复杂,单位“1”不一致时,先把不变量转化成单位“1”,再把变量同单位“1”建立关系,然后思考用方程解决。
……
根据关键句,找出等量关系式。
1、黄球比红球多14个。
2、男生的人数比女生的3/5多3人。
3、一件上衣七五折出售。
4、今年比去年增产两成。
5、两车同时从两地出发,3小时相遇。
6、用长20厘米的铁丝围城一个长方形框架。
列方程解决问题
1、小丽家的草莓去年收获500千克,今年比去年增产两成,今年收获多少千克?
2、一台电脑打八五折后售价为2975元,这台电视机原价多少元?
3、湖北丹江口水库2014年蓄水量达290亿立方米,比北京密云水库蓄水量的26倍还多4亿立方米,密云水库的蓄水量是多少?
4、红球的个数是黄球的3/5,黄球比红球多14个,红球和黄球各有多少个?
5、一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只,如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
逸夫小学 曹会静
思考:
1、用字母可以表示什么?
2、你还能举个例子吗?
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人
s=vt
V圆柱=Sh
a+b=b+a
用字母可以表示具体的数量
1、小明今年a岁,妈妈比她大b岁,妈妈今年( )岁。
2、m表示一个偶数,与它相邻的两个偶数是( )和( )。
3、水果店有b千克苹果,一共要装6箱,平均每箱装( )千克。
4、一只青蛙每天吃a只害虫,100天吃( )只害虫。
a+b
m—2
m+2
b÷6
100a
思考:
1、含有字母的式子中简写的规则?
2、在省略乘号时要注意什么?
1、数字和字母相乘以及字母和字母相乘可以省略乘号,
或者写成“·”。
2、注意点:
a、省略乘号时,数字要写在字母的前面。
1可以省略不写。
例如:a×4=4a,b×1=b
b、两个a相乘可以写出a的平方。a×a=a?。
用字母表示数可以简明地表达数量关系
例如:
用s表示路程,v表示速度,t表示时间,那么
s=vt
c=at
如果工作总量用字母c表示,工作时间用t表示,工作效率用a表示,那么
用字母表示正比例关系:
用字母表示反比例关系:
用字母表示平面图形计算公式
a
a
a
a
b
a
h
d
r
a
b
h
a
h
s
s
h
用字母表示立体图形计算公式
S=(ab+ah+bh)×2 S=6a? S=ch+2S
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
用字母表示运算定律和性质
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷ (b×c)
计算方法
cm、kg、m?……
计量单位
ABB ABB ABB……
一种规律
除法与分数的关系
因倍数
三、巩固练习
1. 连线。
比a多3的数
比a少3的数
3个a相加的和
a的3倍
a?
3a
a+3
a-3
3个a相乘的积
1.9+7=8.9 3x+6>9 x-1.5=1
x+ <12 x+20%x=3.6 2x+5.6=9.4
② ③
④ ⑤ ⑥
判断哪些是方程
请你回顾一下以下知识:
1、什么是方程?方程与等式有什么联系和区别?
2、等式的性质是什么?
3、什么是解方程?什么是方程的解?他们有什么区别?
4、解方程的依据是什么?
x-1.5=1
x+20%x=3.6 2x+5.6=9.4
1、什么是方程?方程与等式有什么关系?
含有未知数的等式叫方程。
方程一定是等式,但等式不一定是方程。
等式的性质:
1、等式两边同时加上或减去同一个数,左右两边仍然相等。
2、等式两边同时乘或除以同一个数(0除外),左右两边仍然相等。
2、什么是方程的解?什么是解方程?他们有什么区别?
方程的解:使方程左右两边相等的未知数的值。
解方程:求方程的解的过程。
一个具体的数
一个过程
3、解方程的依据是什么?
等式的性质
解方程 2x+5.6=9.4
解:
2x+5.6-5.6=9.4-5.6
2x=3.8
2x÷2=3.8÷2
x=1.9
(1)解方程过程中要注意什么?
(2)如何判断x=1.9是否是方程的解?
列方程解决问题。
小平在踢毽子比赛中踢了42下,她踢毽的数量是小云的 。小云踢了多少下?
1、用方程解决问题的基本步骤是什么?
2、其中最关键的是哪一步?
一般分5步:
1)根据题意,解设未知数为x。
2)找出具体的数量,列出等量关系式。
3)根据等量关系式,列出方程。
4)解方程
5)检验并答句。
思考:
1、用方程解决问题的基本步骤是什么?
2、其中最关键的是哪一步?
建议:
1.单位“1”未知时,用方程解决比较简便。
类型一:和倍、差倍的应用题,单位“1”未知用方程解决。
类型二:比谁的几倍多(少)几,单位“1”未知用方程解决。
类型三:甲数比乙数多(少)几分之几或百分之几。单位“1”乙数未知时用方程解决。
2.行程中的相遇问题、相距问题时,求相遇时间或一个车的速度时 ,用方程。
3.题目中数量关系比较复杂,单位“1”不一致时,先把不变量转化成单位“1”,再把变量同单位“1”建立关系,然后思考用方程解决。
……
根据关键句,找出等量关系式。
1、黄球比红球多14个。
2、男生的人数比女生的3/5多3人。
3、一件上衣七五折出售。
4、今年比去年增产两成。
5、两车同时从两地出发,3小时相遇。
6、用长20厘米的铁丝围城一个长方形框架。
列方程解决问题
1、小丽家的草莓去年收获500千克,今年比去年增产两成,今年收获多少千克?
2、一台电脑打八五折后售价为2975元,这台电视机原价多少元?
3、湖北丹江口水库2014年蓄水量达290亿立方米,比北京密云水库蓄水量的26倍还多4亿立方米,密云水库的蓄水量是多少?
4、红球的个数是黄球的3/5,黄球比红球多14个,红球和黄球各有多少个?
5、一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只,如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
