人教版数学七年级下册第七章7.1.2平面直角坐标系 课件(共52张PPT)
文档属性
| 名称 | 人教版数学七年级下册第七章7.1.2平面直角坐标系 课件(共52张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-09 22:11:11 | ||
图片预览







文档简介
课件52张PPT。平面直角坐系
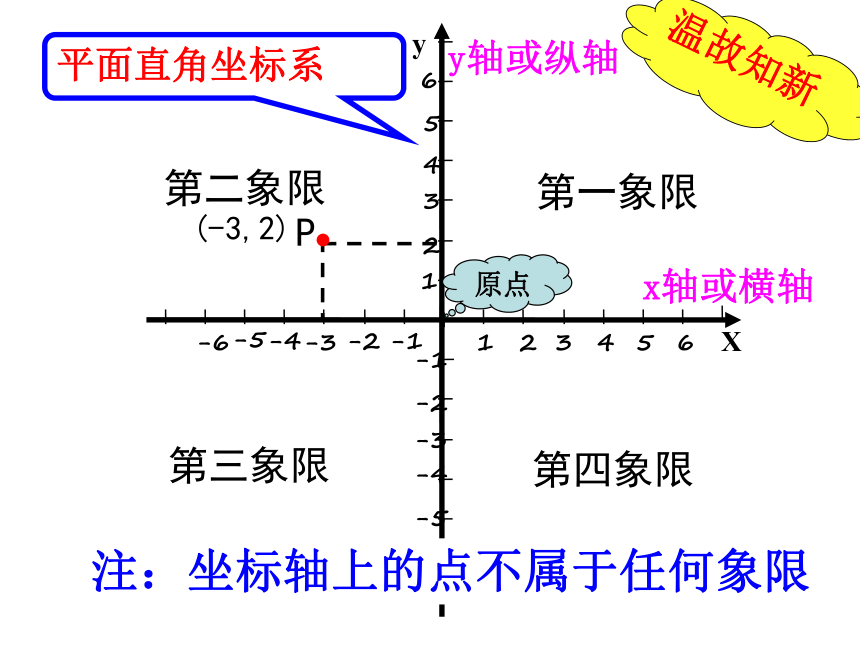
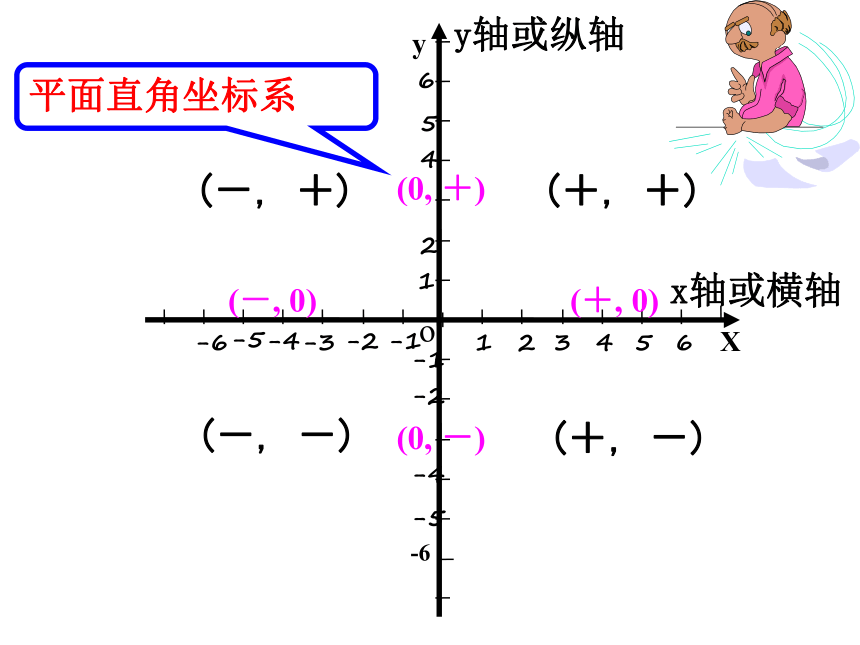
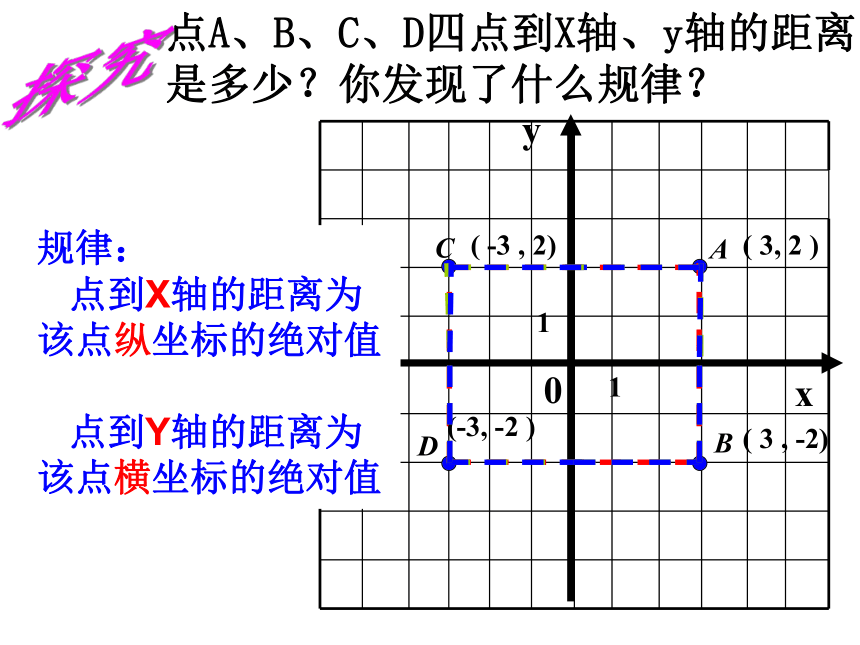
(第2课时)7.1.2x轴或横轴y轴或纵轴平面直角坐标系第一象限第二象限第三象限第四象限P(-3,2)原点注:坐标轴上的点不属于任何象限温故知新5-5-2-4-1241-66y-55-3-44-23-121-66oXx轴或横轴y轴或纵轴平面直角坐标系(+, +)(-, +)(-, -)(+, -)(0, +)(0, -)(+, 0)(-, 0)C(3,4) A(4,-2)B(0,3)D(-4,-3)E(-2,0)F(-4,3)注:坐标轴上的点不属于任何象限试一试BCDA探究xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A、B、C、D四点到X轴、y轴的距离是多少?你发现了什么规律?
规律:
点到X轴的距离为
该点纵坐标的绝对值
点到Y轴的距离为
该点横坐标的绝对值 请快速说出下列各个点到x轴、y轴的距离
A (4, -2) B (0, 3) C (3, 4)
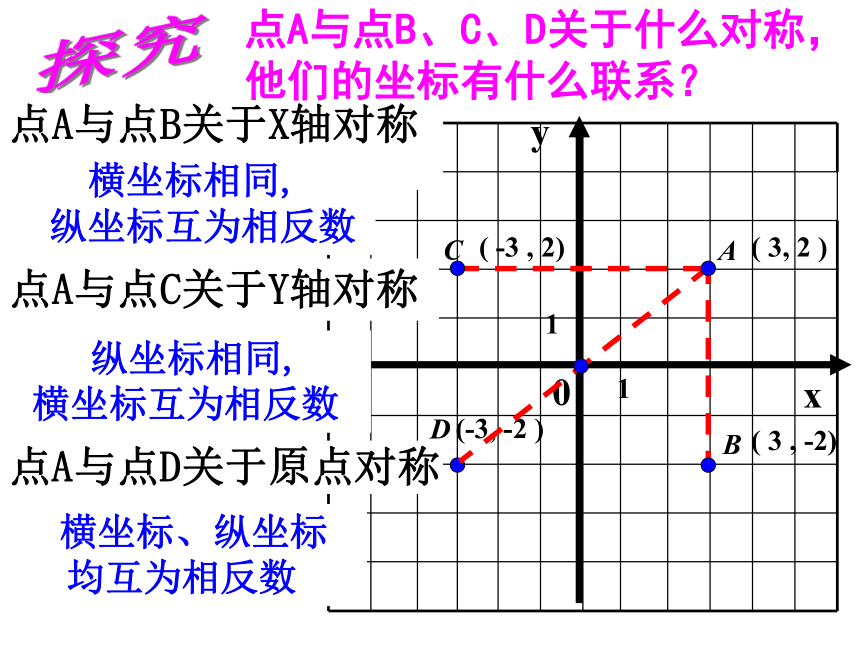
D (-4,-3) E (-2, 0) F (-4, 3)说一说看一看特点:两个图形关于直线对称BCDA探究xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点B关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点C关于Y轴对称 纵坐标相同,
横坐标互为相反数点A与点D关于原点对称 横坐标、纵坐标
均互为相反数点A与点B、C、D关于什么对称,他们的坐标有什么联系?123·OXP(4,3)·B(4,-3)A(-4,3)C(-4,-3) ·你能说出点P关于x轴、y轴、原点的对称点坐标吗?·31425-2-4-1-3·Y若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( )
M点关于原点O的对称点M3( )a,-b- a, b-a,-b练一练你喜欢那种小动物?快来领一只如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
说一说平面直角坐标系中的图形面积问题 练习1:求下列条件下线段AB的长度.
1)A(-6,0),B(-2,0)
2)A(-3,0),B(2,0)
3)A(1,0),B(5,0).
4)A(x1,0),B(x2,0).
5)A(0,y1),B(0 ,y2 ).如图(1), △AOB的面积是多少?问题1yOx图(1)AB4
3
2
11 2 3 4(4,0)(0,3) 坐标 距离 三角形面积线段长度点如图(2), △AOB的面积是多少?问题2yOx图(2)AB4
3
2
11 2 3 4(3,3)(4,0)yABC 练习.
1.已知A(1,4),
B(-4,0),C(2,0).
△ABC的面积是___.
2.若BC的坐标不变,
△ABC的面积为6,点A
的横坐标为-1,那么
点A的坐标为__ _.12O(1,4)(-4,0)(2,0)(-1,2)或(-1,-2)例1 已知A(-2,0),B(4,0),C(x,y) (1)若点C在第二象限,且|x|=4,|y|=4, 求点C的坐标,并求三角形ABC的面积; 分析(1)由点C在第二象限,可知x和y的符号,这样可化简绝对值,从而求点C的坐标,求三角形的面积,关键求点C到AB所在的直线即x轴的距离|y|例1 已知A(-2,0),B(4,0),C(x,y) (2)若点C在第四象限上,且三角形ABC的面积=9,|x|=3,求点C的坐标ABC分析:由三角形的面积可求出C到AB所在的直线距离为3,而点C在第四象限可知它的坐标符号,从而可知y=-32. 点B在哪条直线上运动时, △OAB的面积 保持不变?为什么?yOxAB4
3
2
11 2 3 4(3,3)(4,0)在图(3)中,以OA为边的△OAB的面积为2,试找出符合条件的且顶点是格点的点C,你能找到几个这样的点?(在图中现有的网格中找)y图(3)OxA(2,1)4
3
2
11 2 3 4问题3 Oy4
3
2
11 2 3 4A(2,1)x图(3)Oxy图(4)A(2,1)4
3
2
11 2 3 4OXYA(2,1)4
3
2
11 2 3 4图(5)Oy4
3
2
11 2 3 4A(2,1)x图(6)Oy4
3
2
11 2 3 4A(2,1)x图(7)C(2,2)MN方
法
1Oy4
3
2
11 2 3 4A(2,1)x图(8)D(1,1)EF方
法
2Oy4
3
2
11 2 3 4A(2,1)xE(4,1)F(4,0)图(9)方
法
3Oy4
3
2
11 2 3 4A(2,1)xE(4,1)F(4,0)图(10)G(0,4)方
法
4Oy4
3
2
11 2 3 4A(2,1)xF(4,0)图(11)方
法
5Ox图(12)A(2,1)4
3
2
11 2 3 4y在下图中,以OA为边的△ABO的面积为2,试找出符合条件的点B,你能找到几个这样的点?问题3-1xy1 2 3 4 5 5
4
3
2
1-1A(2,1)OB(0,2)B? (4,4)答:有无数个点,它们在过点(0,2)或(4,0)并与线段OA平行的直线上。ab B? (2,3) C图(13)34 一般的,在平面直角坐标系中,
求已知顶点坐标的多边形面积都可以
通过__ __的方法解决; 在平面直角坐标系中,对于某些图形的面积不易直接求出,我们也可以通过__ _____,使之变为与它等面积的图形。割补等积变换35做一做1.已知△ABC中,A(-1,-2),B(6,2),C(1,3),
求△ABC的面积.y-33637方法238A(-1,-2)B(6,2)C(1,3)E(6,3)F(-1,3)方法339-1
-2xy1 2 3 4 5 6 7 85
4
3
2
1 -2 -1OB(6,2)C(1,3)方法4A(-1,-2)A`B`C`40yx31425-2-1-3O12 3 45-2-16786C(6,8)B(4,0)A(1,-2)78D(1,4) 已知四边形ABCD中,A(1,-2), B(4,0), C(6,8), D(1,4),求四边形ABCD的面积.思考:本节课你学到了什么?关于X轴、Y轴及原点对称的点的坐标特点点到坐标轴的距离点A(a,b)到X轴的距离为
点A(a,b)到Y轴的距离为象限中点的坐标符号的情况及坐标轴上点坐标的特点421.等积变换2.割补法求面积谈谈我们的收获化复杂为简单
化未知为已知方法转化1.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______. 四三y-1知识互动点对典 :2.点 M(- 8,12)到 x轴的距离是_______,到 y轴的距离是________.128知识互动点对典 :3.点A(-2,4)关于x轴的对称点是_________ . (-2,-4)知识互动点对典 :4.点A在x轴上,距离原点4个单位长度,则A点的坐标是_____________ 。(4,0)或(-4,0)方法探究一对一:5.坐标平面内点P(m , 2)与点Q(3 , -2)关于原点对称,则 m =_____; -3方法探究一对一:6.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是__________。(-1.5,-2)方法探究一对一:7.点A(1-a,5),B(3 ,b)
关于y轴对称,则a=___,
b=____。 45知能提升面对面:8.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在_____________。第二或四象限知能提升面对面:9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B知能提升面对面:布置作业:认真思考哦!学法 42—43
(第2课时)7.1.2x轴或横轴y轴或纵轴平面直角坐标系第一象限第二象限第三象限第四象限P(-3,2)原点注:坐标轴上的点不属于任何象限温故知新5-5-2-4-1241-66y-55-3-44-23-121-66oXx轴或横轴y轴或纵轴平面直角坐标系(+, +)(-, +)(-, -)(+, -)(0, +)(0, -)(+, 0)(-, 0)C(3,4) A(4,-2)B(0,3)D(-4,-3)E(-2,0)F(-4,3)注:坐标轴上的点不属于任何象限试一试BCDA探究xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A、B、C、D四点到X轴、y轴的距离是多少?你发现了什么规律?
规律:
点到X轴的距离为
该点纵坐标的绝对值
点到Y轴的距离为
该点横坐标的绝对值 请快速说出下列各个点到x轴、y轴的距离
A (4, -2) B (0, 3) C (3, 4)
D (-4,-3) E (-2, 0) F (-4, 3)说一说看一看特点:两个图形关于直线对称BCDA探究xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点B关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点C关于Y轴对称 纵坐标相同,
横坐标互为相反数点A与点D关于原点对称 横坐标、纵坐标
均互为相反数点A与点B、C、D关于什么对称,他们的坐标有什么联系?123·OXP(4,3)·B(4,-3)A(-4,3)C(-4,-3) ·你能说出点P关于x轴、y轴、原点的对称点坐标吗?·31425-2-4-1-3·Y若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( )
M点关于原点O的对称点M3( )a,-b- a, b-a,-b练一练你喜欢那种小动物?快来领一只如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
说一说平面直角坐标系中的图形面积问题 练习1:求下列条件下线段AB的长度.
1)A(-6,0),B(-2,0)
2)A(-3,0),B(2,0)
3)A(1,0),B(5,0).
4)A(x1,0),B(x2,0).
5)A(0,y1),B(0 ,y2 ).如图(1), △AOB的面积是多少?问题1yOx图(1)AB4
3
2
11 2 3 4(4,0)(0,3) 坐标 距离 三角形面积线段长度点如图(2), △AOB的面积是多少?问题2yOx图(2)AB4
3
2
11 2 3 4(3,3)(4,0)yABC 练习.
1.已知A(1,4),
B(-4,0),C(2,0).
△ABC的面积是___.
2.若BC的坐标不变,
△ABC的面积为6,点A
的横坐标为-1,那么
点A的坐标为__ _.12O(1,4)(-4,0)(2,0)(-1,2)或(-1,-2)例1 已知A(-2,0),B(4,0),C(x,y) (1)若点C在第二象限,且|x|=4,|y|=4, 求点C的坐标,并求三角形ABC的面积; 分析(1)由点C在第二象限,可知x和y的符号,这样可化简绝对值,从而求点C的坐标,求三角形的面积,关键求点C到AB所在的直线即x轴的距离|y|例1 已知A(-2,0),B(4,0),C(x,y) (2)若点C在第四象限上,且三角形ABC的面积=9,|x|=3,求点C的坐标ABC分析:由三角形的面积可求出C到AB所在的直线距离为3,而点C在第四象限可知它的坐标符号,从而可知y=-32. 点B在哪条直线上运动时, △OAB的面积 保持不变?为什么?yOxAB4
3
2
11 2 3 4(3,3)(4,0)在图(3)中,以OA为边的△OAB的面积为2,试找出符合条件的且顶点是格点的点C,你能找到几个这样的点?(在图中现有的网格中找)y图(3)OxA(2,1)4
3
2
11 2 3 4问题3 Oy4
3
2
11 2 3 4A(2,1)x图(3)Oxy图(4)A(2,1)4
3
2
11 2 3 4OXYA(2,1)4
3
2
11 2 3 4图(5)Oy4
3
2
11 2 3 4A(2,1)x图(6)Oy4
3
2
11 2 3 4A(2,1)x图(7)C(2,2)MN方
法
1Oy4
3
2
11 2 3 4A(2,1)x图(8)D(1,1)EF方
法
2Oy4
3
2
11 2 3 4A(2,1)xE(4,1)F(4,0)图(9)方
法
3Oy4
3
2
11 2 3 4A(2,1)xE(4,1)F(4,0)图(10)G(0,4)方
法
4Oy4
3
2
11 2 3 4A(2,1)xF(4,0)图(11)方
法
5Ox图(12)A(2,1)4
3
2
11 2 3 4y在下图中,以OA为边的△ABO的面积为2,试找出符合条件的点B,你能找到几个这样的点?问题3-1xy1 2 3 4 5 5
4
3
2
1-1A(2,1)OB(0,2)B? (4,4)答:有无数个点,它们在过点(0,2)或(4,0)并与线段OA平行的直线上。ab B? (2,3) C图(13)34 一般的,在平面直角坐标系中,
求已知顶点坐标的多边形面积都可以
通过__ __的方法解决; 在平面直角坐标系中,对于某些图形的面积不易直接求出,我们也可以通过__ _____,使之变为与它等面积的图形。割补等积变换35做一做1.已知△ABC中,A(-1,-2),B(6,2),C(1,3),
求△ABC的面积.y-33637方法238A(-1,-2)B(6,2)C(1,3)E(6,3)F(-1,3)方法339-1
-2xy1 2 3 4 5 6 7 85
4
3
2
1 -2 -1OB(6,2)C(1,3)方法4A(-1,-2)A`B`C`40yx31425-2-1-3O12 3 45-2-16786C(6,8)B(4,0)A(1,-2)78D(1,4) 已知四边形ABCD中,A(1,-2), B(4,0), C(6,8), D(1,4),求四边形ABCD的面积.思考:本节课你学到了什么?关于X轴、Y轴及原点对称的点的坐标特点点到坐标轴的距离点A(a,b)到X轴的距离为
点A(a,b)到Y轴的距离为象限中点的坐标符号的情况及坐标轴上点坐标的特点421.等积变换2.割补法求面积谈谈我们的收获化复杂为简单
化未知为已知方法转化1.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______. 四三y-1知识互动点对典 :2.点 M(- 8,12)到 x轴的距离是_______,到 y轴的距离是________.128知识互动点对典 :3.点A(-2,4)关于x轴的对称点是_________ . (-2,-4)知识互动点对典 :4.点A在x轴上,距离原点4个单位长度,则A点的坐标是_____________ 。(4,0)或(-4,0)方法探究一对一:5.坐标平面内点P(m , 2)与点Q(3 , -2)关于原点对称,则 m =_____; -3方法探究一对一:6.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是__________。(-1.5,-2)方法探究一对一:7.点A(1-a,5),B(3 ,b)
关于y轴对称,则a=___,
b=____。 45知能提升面对面:8.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在_____________。第二或四象限知能提升面对面:9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B知能提升面对面:布置作业:认真思考哦!学法 42—43
