六年级下册数学一课一练4.1圆柱和圆锥冀教版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练4.1圆柱和圆锥冀教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 63.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 00:00:00 | ||
图片预览



文档简介
六年级下册数学一课一练-3.1圆柱和圆锥
一、单选题
1.圆柱和圆椎的体积相等,底面积也相等,那么圆柱的高是圆锥的高的(?? )
A.?9倍???????????????????????????????????????????B.?3倍???????????????????????????????????????????C.?
2.一个圆柱的上下底面是(?? )的圆。
A.?完全相等??????????????????????????????????B.?不完全相等??????????????????????????????????C.?不确定
3.如果圆柱的侧面展开后是一个正方形,那么这个圆柱的(? )一定和高相等.
A.?直径???????????????????????????????????????B.?半径???????????????????????????????????????C.?底面周长
4.做一个无盖的圆柱形水桶,求至少需要多少铁皮,就是求水桶的(?? )。
A.?底面积?????????????????????????B.?侧面积?????????????????????????C.?表面积?????????????????????????D.?侧面积+一个底面积
5.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图),将圆柱形状容器中的水倒入第 ??????个圆锥形状的容器,正好可以倒满.(?? )
A.?????????????????????B.?????????????????????C.?
6.下面图形以AB边为轴旋转后会形成图形(??? )。??
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
二、判断题
7.圆锥的体积等于和它等底等高的圆柱体积 。
8.圆锥的底面积扩大4倍,高不变,体积也扩大4倍。
9.底面积和高分别相等的长方体、正方体、圆柱的体积一定相等.
10. 圆柱的体积比与它等底等高的圆锥的体积多2倍________.(判断对错)
11.“求做圆柱形通风管需要多少铁皮”是求圆柱的侧面积。(判断对错)
三、填空题
12.圆锥的底面是一个________,把圆锥的侧面展开是一个________.
13.将体积为78.5dm3的铁块熔铸成一个底面直径为10dm的圆锥体零件,圆锥的高是________dm.
14.一个圆柱形的铁块底面直径长40厘米,高3分米,该圆柱体的体积是________立方分米。将这个圆柱形铁块锻造成底面相同的圆锥,圆锥的高是________分米。
15.( )滚得快,而且它的两个相对的面是平平的.
A.?球体?????????????????????????????????B.?长方体?????????????????????????????????C.?圆柱体?????????????????????????????????D.?正方体
16.圆锥的体积等于和它等底等高的圆柱体积的________?.
17.一个圆柱和一个圆锥等高,底面积之比是2:3,则体积之比是________。
四、计算题
18.一个圆柱形钢材,截去10厘米长的一段后,表面积减少了314平方厘米,体积减少了多少立方厘米?
五、解答题
19.求下图中立体图形的表面积和体积。
20.某小区准备在楼房外安装一种长方体的铁皮漏水管以便于雨季排水。这种漏水管的长是36米,底面是边长为1分米的正方形。制作这样的漏水管20个至少需要多少平方米的铁皮?
六、综合题
21.计算下面图形的体积。(单位:cm)
(1)?
(2)
七、应用题
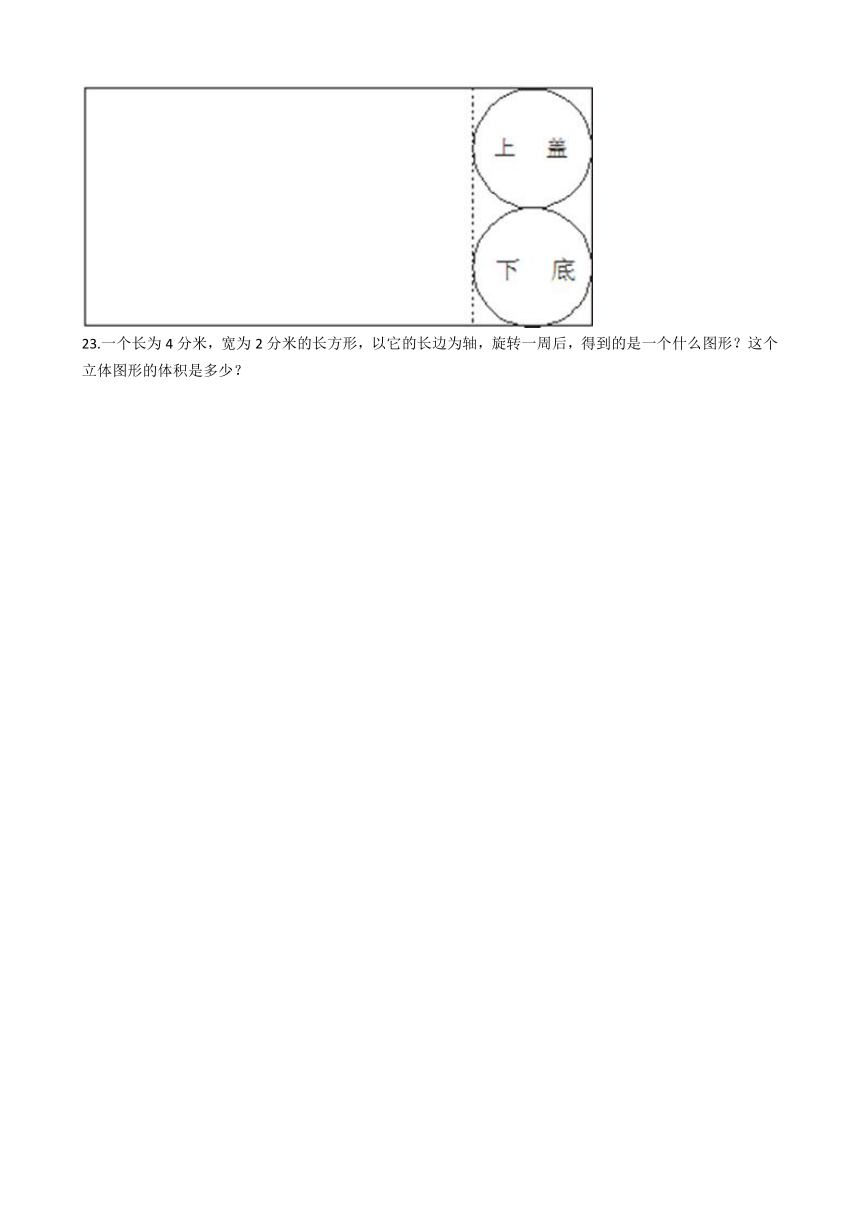
22.张师傅用一张长方形铁皮按下图剪开正好能制成一个底面半径为2分米的铁皮油桶.请你计算一下这张铁片的面积至少是多少平方分米才行?
23.一个长为4分米,宽为2分米的长方形,以它的长边为轴,旋转一周后,得到的是一个什么图形?这个立体图形的体积是多少?
答案解析部分
一、单选题
1.【答案】C
【解析】【解答】假设圆柱和圆锥的体积都是V,底面积都是S,则圆柱的高是:V÷S=,圆锥的高是:3V÷S=,÷=×=. 故答案为:C.
【分析】圆柱和圆椎的体积相等,底面积也相等,那么圆柱的高是圆锥的高的,据此解答.
2.【答案】 A
【解析】【解答】一个圆柱的上下底面是完全相等的圆. 故答案为:A.
【分析】根据圆柱的特征可知,圆柱是由两个底面和一个侧面组成的,圆柱体的两个底面是完全相同的两个圆,两底间距离是高,有无数条高与对称轴.
3.【答案】C
【解析】【解答】根据圆柱体的侧面展开图的长、宽与圆柱体的底面周长和高的关系,如果圆柱的侧面展开后是一个正方形,那么这个圆柱的底面周长和高一定相等.
答:这个圆柱的底面周长和高一定相等。
【分析】根据圆柱体的特征,它的上下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形或正方形,长方形的长等于圆柱体的底面周长,宽等于圆柱体的高;由此解答。
故选:C
4.【答案】 D
【解析】【解答】解:无盖的圆柱形水桶,即说明没有上底面,故做一个无盖的圆柱形水桶,求至少需要多少铁皮,就是求水桶的侧面积加上一个底面积。 故答案为:D。 【分析】圆柱的表面积=侧面积+两个底面积。
5.【答案】 C
【解析】【解答】3.14×(20÷2)2×6=1884,×3.14×(20÷2)2×18=1884 故答案为:C。
【分析】解答此题先用圆柱的体积公式求出水的体积,然后求出圆锥的体积,找到和圆柱内水的体积相同的圆锥的体积即可解答此题。
6.【答案】 A
【解析】【解答】以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体; 故选:A.
【分析】本题考点:圆锥的特征;圆柱的特征. 此题考查了点、线、面、体,重在体现面动成体,考查学生立体图形的空间想象能力及分析问题、解决问题的能力.
以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体;据此解答.
二、判断题
7.【答案】 正确
【解析】【解答】圆锥的体积等于和它等底等高的圆柱体积的,原题说法正确. 故答案为:正确.
【分析】等底等高的圆柱体积是圆锥体积的3倍,圆锥体积是圆柱体积的,据此判断.
8.【答案】正确
【解析】解答:由题意, 。
分析:由圆锥的体积公式进行换算即得。
9.【答案】 正确
【解析】【解答】解:底面积和高分别相等的长方体、正方体、圆柱,由于它们的体积都是用底面积×高求得,所以它们的体积也是相等的;
故答案为:正确.
【分析】底面积和高分别相等的长方体、正方体、圆柱,它们的体积都是用底面积乘高得来,所以它们的体积也一定相等,原题说法是正确的.此题是考查体积的计算公式,求长方体、正方体、圆柱的体积都可用V=sh解答.
10.【答案】正确
【解析】【解答】解:因为圆柱的体积等于和它等底等高的圆锥体积的3倍,
所以圆柱的体积比与它等底等高的圆锥的体积多:(3﹣1)=2倍;
故答案为:正确.
【分析】因为圆柱的体积等于和它等底等高的圆锥体积的3倍,把圆锥的体积看作1,则圆柱的体积是3,则圆柱的体积比与它等底等高的圆锥的体积多(3﹣1)=2倍,据此判断即可.
11.【答案】正确
【解析】【解答】“做圆柱形通风管需要多少铁皮”是求这个圆柱的侧面积。 故答案为:正确。 【分析】本题考点:圆柱的展开图。 此题主要考查圆柱的展开图,关键明白圆柱形通风管的表面积即为其侧面积。 圆柱的表面积为侧面积加两个底面的面,而圆柱形通风管的表面积则去掉圆柱的两个底面的面积,即只求其侧面积即可。
三、填空题
12.【答案】 圆;扇形
【解析】【解答】圆锥的底面是一个圆,把圆锥的侧面展开是一个扇形. 故答案为:圆;扇形.
【分析】圆锥的侧面展开是一个扇形,只有下底,下底面是一个圆,所以从正上面看是一个圆,从侧面水平看是一个等腰三角形, 可以由等腰三角形绕底边的高旋转得到,也可以由直角三角形绕一个直角边旋转得到,据此解答.
13.【答案】3
【解析】【解答】解:78.5×3÷[3.14×(10÷2)2]
=235.5÷78.5
=3(dm);
答:圆锥的高是3dm.
故答案为:3.
【分析】根据题意,将一个体积为78.5dm3的铁块熔铸成一个底面直径为10dm的圆锥体零件,那么铸成的圆锥的体积还是原来的体积78.5dm3 , 由圆锥的体积公式V= πr2h,那么h=3V÷(πr2),先由底面直径求出半径,再将数据代入公式计算即可.这道题主要考查等积变形和圆锥体积公式的灵活应用.
14.【答案】37.68 ;9
【解析】【解答】解:40厘米=4分米;圆柱的体积:3.14×(4÷2)2×3=37.68(立方分米); 37.68×3÷[3.14×(4÷2)2] =113.04÷12.56 =9(分米) 故答案为:37.67;9
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×;根据圆柱的体积公式计算圆柱的体积,用圆柱的体积乘3后除以圆锥的底面积即可求出圆锥的高.
15.【答案】C
【解析】【解答】圆柱体滚得快,而且它的两个相对的面是平平的.选C.
【分析】圆柱上下一样粗细,它的上下两面是圆形,平平的,如果平放在桌上能滚动,立在桌上不能滚动.
16.【答案】 ?
【解析】【解答】根据圆柱和圆锥的体积公式可知,圆锥的体积等于和它等底等高的圆柱体积的. 故答案为:
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,所以等底等高的圆锥的体积是圆柱体积的,或者说等底等高的圆柱体积是圆锥体积的3倍.
17.【答案】2:1
【解析】【解答】设圆柱的底面积为2a , 则圆锥的底面积为3a , 圆柱的体积为:2a h,圆锥的体积为 ×3a h=a h,则圆柱与圆锥的体积之比是2:1。 故答案为:2:1【分析】根据题意,设圆柱的底面积为2a , 则圆锥的底面积为3a , 依据圆柱和圆锥的体积公式:圆柱的体积=底面积×高,圆锥的体积=×底面积×高,当高相等时,表示出圆柱和圆锥的体积,并相比,据此解答.
四、计算题
18.【答案】解答:圆柱的底面半径为:314÷10÷3.14÷2=5(厘米)
则截去部分的体积是:3.14×52×10=785〔立方厘米)
答:体积减少了785立方厘米。
【解析】【分析】根据圆柱的切割特点可知,表面积减少314平方厘米,就是截去的高为10厘米的圆柱的侧面积,由此可以求得这个圆柱的底面半径,再利用圆柱的体积公式计算切去部分的体积即是减少的体积。
五、解答题
19.【答案】解:表面积:3.14 X(4÷2)2×2+(2 X 3.14+3×3.14+4×3.14)×0.5=39.25(平方米)
体积:3.14×(2÷2)2×0.5+3.14×(3÷2)2X0.5+3.14×(4÷2)2×0.5=11.3825(立方米)。
【解析】【分析】整个图形上下面面积相等,都是直径4米的圆面积,然后再加上三个圆柱的侧面积就是立体图形的表面积;圆柱的体积=底面积×高,把三个圆柱的体积相加即可。
20.【答案】解:1分米=0.1米 0.1×4×36×20 =0.4×720 =288(平方米) 答:制作这样的漏水管20个至少需要288平方米的铁皮.
【解析】【分析】漏水管是圆柱,没有底面,圆柱的侧面=底面周长×高,根据圆柱的侧面积公式计算出一个水管需要铁皮的面积,再乘20即可,注意统一单位.
六、综合题
21.【答案】(1)解:3.14×32×5.4=152.604(cm3) (2)解:3.14×(8÷2)2×6× =3.14×16×2 =100.48(cm3)
【解析】【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,根据公式分别计算即可.
七、应用题
22.【答案】解:长方形的宽:2×2×2=8(分米);
长方形的长:3.14×2×2+2×2=12.56+4=16.56(分米);
长方形的面积:16.56×8=132.48(平方分米);
答:这张铁皮的面积至少132.48平方分米。
【解析】【分析】要求这张铁皮的面积至少是多少平方分米,也就是求这个长方形的面积,这个长方形的宽是这两个圆的直径和,也就是4个半径,即宽=4×半径,长=底面周长+2×半径,根据长方形的面积=长×宽,计算出答案。
23.【答案】解:3.14×22×4,
=3.14×4×4,
=50.24(立方分米),
答:这个立体图形的体积是50.24立方分米。
【解析】【分析】一个长方形绕着长为轴旋转一周,可以得到一个底面半径为2分米,高为4分米的圆柱体,由此利用圆柱的体积公式即可解答。
一、单选题
1.圆柱和圆椎的体积相等,底面积也相等,那么圆柱的高是圆锥的高的(?? )
A.?9倍???????????????????????????????????????????B.?3倍???????????????????????????????????????????C.?
2.一个圆柱的上下底面是(?? )的圆。
A.?完全相等??????????????????????????????????B.?不完全相等??????????????????????????????????C.?不确定
3.如果圆柱的侧面展开后是一个正方形,那么这个圆柱的(? )一定和高相等.
A.?直径???????????????????????????????????????B.?半径???????????????????????????????????????C.?底面周长
4.做一个无盖的圆柱形水桶,求至少需要多少铁皮,就是求水桶的(?? )。
A.?底面积?????????????????????????B.?侧面积?????????????????????????C.?表面积?????????????????????????D.?侧面积+一个底面积
5.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图),将圆柱形状容器中的水倒入第 ??????个圆锥形状的容器,正好可以倒满.(?? )
A.?????????????????????B.?????????????????????C.?
6.下面图形以AB边为轴旋转后会形成图形(??? )。??
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
二、判断题
7.圆锥的体积等于和它等底等高的圆柱体积 。
8.圆锥的底面积扩大4倍,高不变,体积也扩大4倍。
9.底面积和高分别相等的长方体、正方体、圆柱的体积一定相等.
10. 圆柱的体积比与它等底等高的圆锥的体积多2倍________.(判断对错)
11.“求做圆柱形通风管需要多少铁皮”是求圆柱的侧面积。(判断对错)
三、填空题
12.圆锥的底面是一个________,把圆锥的侧面展开是一个________.
13.将体积为78.5dm3的铁块熔铸成一个底面直径为10dm的圆锥体零件,圆锥的高是________dm.
14.一个圆柱形的铁块底面直径长40厘米,高3分米,该圆柱体的体积是________立方分米。将这个圆柱形铁块锻造成底面相同的圆锥,圆锥的高是________分米。
15.( )滚得快,而且它的两个相对的面是平平的.
A.?球体?????????????????????????????????B.?长方体?????????????????????????????????C.?圆柱体?????????????????????????????????D.?正方体
16.圆锥的体积等于和它等底等高的圆柱体积的________?.
17.一个圆柱和一个圆锥等高,底面积之比是2:3,则体积之比是________。
四、计算题
18.一个圆柱形钢材,截去10厘米长的一段后,表面积减少了314平方厘米,体积减少了多少立方厘米?
五、解答题
19.求下图中立体图形的表面积和体积。
20.某小区准备在楼房外安装一种长方体的铁皮漏水管以便于雨季排水。这种漏水管的长是36米,底面是边长为1分米的正方形。制作这样的漏水管20个至少需要多少平方米的铁皮?
六、综合题
21.计算下面图形的体积。(单位:cm)
(1)?
(2)
七、应用题
22.张师傅用一张长方形铁皮按下图剪开正好能制成一个底面半径为2分米的铁皮油桶.请你计算一下这张铁片的面积至少是多少平方分米才行?
23.一个长为4分米,宽为2分米的长方形,以它的长边为轴,旋转一周后,得到的是一个什么图形?这个立体图形的体积是多少?
答案解析部分
一、单选题
1.【答案】C
【解析】【解答】假设圆柱和圆锥的体积都是V,底面积都是S,则圆柱的高是:V÷S=,圆锥的高是:3V÷S=,÷=×=. 故答案为:C.
【分析】圆柱和圆椎的体积相等,底面积也相等,那么圆柱的高是圆锥的高的,据此解答.
2.【答案】 A
【解析】【解答】一个圆柱的上下底面是完全相等的圆. 故答案为:A.
【分析】根据圆柱的特征可知,圆柱是由两个底面和一个侧面组成的,圆柱体的两个底面是完全相同的两个圆,两底间距离是高,有无数条高与对称轴.
3.【答案】C
【解析】【解答】根据圆柱体的侧面展开图的长、宽与圆柱体的底面周长和高的关系,如果圆柱的侧面展开后是一个正方形,那么这个圆柱的底面周长和高一定相等.
答:这个圆柱的底面周长和高一定相等。
【分析】根据圆柱体的特征,它的上下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形或正方形,长方形的长等于圆柱体的底面周长,宽等于圆柱体的高;由此解答。
故选:C
4.【答案】 D
【解析】【解答】解:无盖的圆柱形水桶,即说明没有上底面,故做一个无盖的圆柱形水桶,求至少需要多少铁皮,就是求水桶的侧面积加上一个底面积。 故答案为:D。 【分析】圆柱的表面积=侧面积+两个底面积。
5.【答案】 C
【解析】【解答】3.14×(20÷2)2×6=1884,×3.14×(20÷2)2×18=1884 故答案为:C。
【分析】解答此题先用圆柱的体积公式求出水的体积,然后求出圆锥的体积,找到和圆柱内水的体积相同的圆锥的体积即可解答此题。
6.【答案】 A
【解析】【解答】以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体; 故选:A.
【分析】本题考点:圆锥的特征;圆柱的特征. 此题考查了点、线、面、体,重在体现面动成体,考查学生立体图形的空间想象能力及分析问题、解决问题的能力.
以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体;据此解答.
二、判断题
7.【答案】 正确
【解析】【解答】圆锥的体积等于和它等底等高的圆柱体积的,原题说法正确. 故答案为:正确.
【分析】等底等高的圆柱体积是圆锥体积的3倍,圆锥体积是圆柱体积的,据此判断.
8.【答案】正确
【解析】解答:由题意, 。
分析:由圆锥的体积公式进行换算即得。
9.【答案】 正确
【解析】【解答】解:底面积和高分别相等的长方体、正方体、圆柱,由于它们的体积都是用底面积×高求得,所以它们的体积也是相等的;
故答案为:正确.
【分析】底面积和高分别相等的长方体、正方体、圆柱,它们的体积都是用底面积乘高得来,所以它们的体积也一定相等,原题说法是正确的.此题是考查体积的计算公式,求长方体、正方体、圆柱的体积都可用V=sh解答.
10.【答案】正确
【解析】【解答】解:因为圆柱的体积等于和它等底等高的圆锥体积的3倍,
所以圆柱的体积比与它等底等高的圆锥的体积多:(3﹣1)=2倍;
故答案为:正确.
【分析】因为圆柱的体积等于和它等底等高的圆锥体积的3倍,把圆锥的体积看作1,则圆柱的体积是3,则圆柱的体积比与它等底等高的圆锥的体积多(3﹣1)=2倍,据此判断即可.
11.【答案】正确
【解析】【解答】“做圆柱形通风管需要多少铁皮”是求这个圆柱的侧面积。 故答案为:正确。 【分析】本题考点:圆柱的展开图。 此题主要考查圆柱的展开图,关键明白圆柱形通风管的表面积即为其侧面积。 圆柱的表面积为侧面积加两个底面的面,而圆柱形通风管的表面积则去掉圆柱的两个底面的面积,即只求其侧面积即可。
三、填空题
12.【答案】 圆;扇形
【解析】【解答】圆锥的底面是一个圆,把圆锥的侧面展开是一个扇形. 故答案为:圆;扇形.
【分析】圆锥的侧面展开是一个扇形,只有下底,下底面是一个圆,所以从正上面看是一个圆,从侧面水平看是一个等腰三角形, 可以由等腰三角形绕底边的高旋转得到,也可以由直角三角形绕一个直角边旋转得到,据此解答.
13.【答案】3
【解析】【解答】解:78.5×3÷[3.14×(10÷2)2]
=235.5÷78.5
=3(dm);
答:圆锥的高是3dm.
故答案为:3.
【分析】根据题意,将一个体积为78.5dm3的铁块熔铸成一个底面直径为10dm的圆锥体零件,那么铸成的圆锥的体积还是原来的体积78.5dm3 , 由圆锥的体积公式V= πr2h,那么h=3V÷(πr2),先由底面直径求出半径,再将数据代入公式计算即可.这道题主要考查等积变形和圆锥体积公式的灵活应用.
14.【答案】37.68 ;9
【解析】【解答】解:40厘米=4分米;圆柱的体积:3.14×(4÷2)2×3=37.68(立方分米); 37.68×3÷[3.14×(4÷2)2] =113.04÷12.56 =9(分米) 故答案为:37.67;9
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×;根据圆柱的体积公式计算圆柱的体积,用圆柱的体积乘3后除以圆锥的底面积即可求出圆锥的高.
15.【答案】C
【解析】【解答】圆柱体滚得快,而且它的两个相对的面是平平的.选C.
【分析】圆柱上下一样粗细,它的上下两面是圆形,平平的,如果平放在桌上能滚动,立在桌上不能滚动.
16.【答案】 ?
【解析】【解答】根据圆柱和圆锥的体积公式可知,圆锥的体积等于和它等底等高的圆柱体积的. 故答案为:
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,所以等底等高的圆锥的体积是圆柱体积的,或者说等底等高的圆柱体积是圆锥体积的3倍.
17.【答案】2:1
【解析】【解答】设圆柱的底面积为2a , 则圆锥的底面积为3a , 圆柱的体积为:2a h,圆锥的体积为 ×3a h=a h,则圆柱与圆锥的体积之比是2:1。 故答案为:2:1【分析】根据题意,设圆柱的底面积为2a , 则圆锥的底面积为3a , 依据圆柱和圆锥的体积公式:圆柱的体积=底面积×高,圆锥的体积=×底面积×高,当高相等时,表示出圆柱和圆锥的体积,并相比,据此解答.
四、计算题
18.【答案】解答:圆柱的底面半径为:314÷10÷3.14÷2=5(厘米)
则截去部分的体积是:3.14×52×10=785〔立方厘米)
答:体积减少了785立方厘米。
【解析】【分析】根据圆柱的切割特点可知,表面积减少314平方厘米,就是截去的高为10厘米的圆柱的侧面积,由此可以求得这个圆柱的底面半径,再利用圆柱的体积公式计算切去部分的体积即是减少的体积。
五、解答题
19.【答案】解:表面积:3.14 X(4÷2)2×2+(2 X 3.14+3×3.14+4×3.14)×0.5=39.25(平方米)
体积:3.14×(2÷2)2×0.5+3.14×(3÷2)2X0.5+3.14×(4÷2)2×0.5=11.3825(立方米)。
【解析】【分析】整个图形上下面面积相等,都是直径4米的圆面积,然后再加上三个圆柱的侧面积就是立体图形的表面积;圆柱的体积=底面积×高,把三个圆柱的体积相加即可。
20.【答案】解:1分米=0.1米 0.1×4×36×20 =0.4×720 =288(平方米) 答:制作这样的漏水管20个至少需要288平方米的铁皮.
【解析】【分析】漏水管是圆柱,没有底面,圆柱的侧面=底面周长×高,根据圆柱的侧面积公式计算出一个水管需要铁皮的面积,再乘20即可,注意统一单位.
六、综合题
21.【答案】(1)解:3.14×32×5.4=152.604(cm3) (2)解:3.14×(8÷2)2×6× =3.14×16×2 =100.48(cm3)
【解析】【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,根据公式分别计算即可.
七、应用题
22.【答案】解:长方形的宽:2×2×2=8(分米);
长方形的长:3.14×2×2+2×2=12.56+4=16.56(分米);
长方形的面积:16.56×8=132.48(平方分米);
答:这张铁皮的面积至少132.48平方分米。
【解析】【分析】要求这张铁皮的面积至少是多少平方分米,也就是求这个长方形的面积,这个长方形的宽是这两个圆的直径和,也就是4个半径,即宽=4×半径,长=底面周长+2×半径,根据长方形的面积=长×宽,计算出答案。
23.【答案】解:3.14×22×4,
=3.14×4×4,
=50.24(立方分米),
答:这个立体图形的体积是50.24立方分米。
【解析】【分析】一个长方形绕着长为轴旋转一周,可以得到一个底面半径为2分米,高为4分米的圆柱体,由此利用圆柱的体积公式即可解答。
