六年级下册数学一课一练-4.圆柱和圆锥冀教版(2014秋) (含解析答案)
文档属性
| 名称 | 六年级下册数学一课一练-4.圆柱和圆锥冀教版(2014秋) (含解析答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 44.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 10:58:32 | ||
图片预览



文档简介
六年级下册数学一课一练-3.圆柱和圆锥
一、单选题
1.一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是()立方厘米。
A.? n?????????????????????????????????????????/B.?2n?????????????????????????????????????????/C.?3n?????????????????????????????????????????/D.?4n
2.当一个圆柱的底面________和高相等时,展开这个圆柱的侧面,可以得到一个正方形.(?? )
A.?直径?????????????????????????????????????????/B.?半径?????????????????????????????????????????/C.?周长
3.一个圆柱形纸筒,底面周长和高都是5厘米,把它的侧面沿着高剪开,所得到的侧面展开图是( )
A.?长方形????????????????????????????????????B.?正方形????????????????????????????????????C.?圆????????????????????????????????????D.?梯形
4.一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的(????? )。
A.?2倍???????????????????????????????????????B.?4倍???????????????????????????????????????C.?6倍???????????????????????????????????????D.?8倍
5.一个圆锥体零件,底面直径20厘米,高15厘米.它的体积是(?? )
A.?314立方厘米?????????????????/B.?1570立方厘米?????????????????/C.?4710立方厘米?????????????????/D.?2620立方厘米
6.一个圆锥和一个圆柱的底面积之比是3:2,高之比是1:3,它们的体积比(??? )
A.?1:6?????????????????????????????????????????B.?1:2?????????????????????????????????????????C.?3:2
二、判断题
7.圆柱的表面积用“底面周长×高”来计算。
8.如果一个圆柱体与一个长方体的底面积和高都相等,那么它们的体积也一定相等.
9.等底等高的圆柱体比圆锥体的体积大16立方分米, 这个圆锥的体积是8立方分米。
10.圆锥体的体积是8立方厘米,高是2厘米,底面积是12平方厘米.
11.任意两个相同的圆和一个曲面就可以组成一个圆柱。
三、填空题
12.两个等高的圆柱和圆锥,如果圆柱与圆锥的底面半径这比是2:1,那么圆柱和圆锥的体积最简比是________:________。
13.在一个体积是14.13ml且装满水的圆柱形容器里,放入一个等底等高的圆锥体后.容器里还有水________?ml.
14.一个圆锥形沙堆的底面半径是5米,高是3米.如果每立方米沙重2吨,这堆沙共重________
15.? 一个圆锥底面面积是18厘米,高是5厘米,它的体积是________立方厘米。
16.制作下面圆柱体的物体,至少要用________平方米的铁皮?
/
17.砌一个圆柱形沼气池,底面直径是4米,深是2米。在池的周围与底面抹上水泥,抹水泥部分的面积是________平方米。
18.一个圆柱和一个圆锥,底面积和体积分别相等,圆锥的高是9cm,圆柱的高是________?cm.
四、计算题
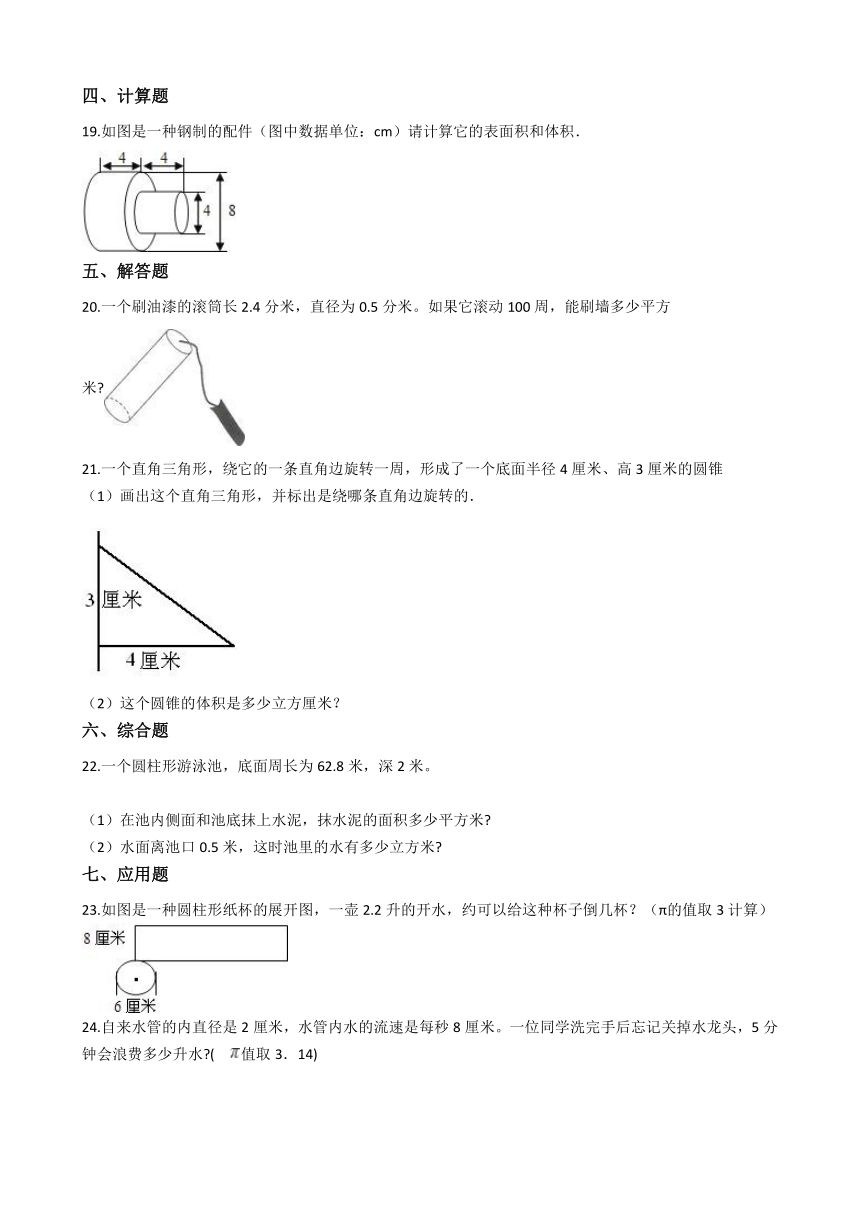
19.如图是一种钢制的配件(图中数据单位:cm)请计算它的表面积和体积. /
五、解答题
20.一个刷油漆的滚筒长2.4分米,直径为0.5分米。如果它滚动100周,能刷墙多少平方米?/
21.一个直角三角形,绕它的一条直角边旋转一周,形成了一个底面半径4厘米、高3厘米的圆锥
(1)画出这个直角三角形,并标出是绕哪条直角边旋转的.
/
(2)这个圆锥的体积是多少立方厘米?
六、综合题
22.一个圆柱形游泳池,底面周长为62.8米,深2米。
(1)在池内侧面和池底抹上水泥,抹水泥的面积多少平方米?
(2)水面离池口0.5米,这时池里的水有多少立方米?
七、应用题
23.如图是一种圆柱形纸杯的展开图,一壶2.2升的开水,约可以给这种杯子倒几杯?(π的值取3计算) /
24.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米。一位同学洗完手后忘记关掉水龙头,5分钟会浪费多少升水?( /值取3.14)
答案解析部分
一、单选题
1.【答案】 C
【解析】解答:由题意可知,设圆柱的体积、圆锥的体积分别是 /,由题意可知: /
分析:圆锥的体积公式和圆柱的体积公式。
2.【答案】 C
【解析】【解答】圆柱的侧面展开后如果是一个正方形,说明圆柱的底面周长和高相等. 故答案为:C 【分析】圆柱的侧面展开是一个长方形或正方形,长方形或正方形的一条边的长度与底面周长相等,另一条边的长度与高相等;如果底面周长与高相等时才是正方形.
3.【答案】B
【解析】【解答】解:因为底面周长和高都是5厘米,底面周长与高相等,所以它的侧面展开图是正方形.
故选;B.
【分析】任何圆柱的侧面展开后是一个长方形或正方形,若是长方形,则它的长等于圆柱的底面周长,宽等于圆柱的高;若是正方形,则长与宽相等,即圆柱的底面周长与高相等,据此解答.
4.【答案】 B
【解析】【解答】解:一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的2×2=4倍。 故答案为:B。 【分析】圆锥的体积=/πr2h,当它的高不变,底面半径扩大到原来的2倍后,现在圆锥的体积=/π(r×2)2h=/πr2h×4=原来圆锥的体积×4。
5.【答案】 B
【解析】【解答】3.14×(20÷2)2×15×/ =3.14×100×5 =1570(立方厘米) 故答案为:B
【分析】圆锥的体积=底面积×高×/,由此根据圆锥的体积公式列式计算求出体积即可.
6.【答案】 A
【解析】【解答】解:设它们的高分别为3H、H,
圆柱的体积=2×3H=6H,
圆锥的体积= /×3×H=H,
圆锥与圆柱的体积之比是H:6H=1:6.
故选:A.
【分析】由“一个圆锥和圆柱的底面积之比是3:2”可知把圆柱的底面积看作2份,圆锥的底面积就是3份,设它们的高为H,高之比是1:3,根据圆柱的体积=SH和圆锥的体积= /SH,分别算出体积,最后求出比.
二、判断题
7.【答案】错误
【解析】【解答】圆柱的表面积用底面周长×高+两个底面的面积。 故答案为:错误。
【分析】这道题考查的是圆柱的表面积的知识,圆柱的表面积是圆柱的3个面的面积,即一个侧面的面积和两个底面的面积的和,据此分析判断即可。
8.【答案】正确
【解析】【解答】解:底面积和高分别相等的长方体、圆柱,由于它们的体积都是用底面积×高求得,所以它们的体积也是相等的.
故答案为:正确.
【分析】底面积和高分别相等的长方体、圆柱,它们的体积都是用底面积乘高得来,所以它们的体积也一定相等,依此即可求解.
9.【答案】正确
【解析】【解答】解:16÷2=8(立方分米),原题说法正确。 故答案为:正确。 【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×/, 等底等高的圆柱体积是圆锥体积的3倍,圆柱体积比圆锥大2倍,因此用大的体积除以大的倍数即可求出圆锥的体积。
10.【答案】 正确
【解析】【解答】解:8÷ /÷2
=8×3÷2
=24÷2
=12(平方厘米);
答:它的底面积是12平方厘米.
故答案为:正确.
【分析】根据圆锥的体积公式,v= /sh,已知圆锥体的体积是8立方厘米,高是2厘米,求它的底面积.用体积÷ /÷高;由此列式解答.
11.【答案】 错误
【解析】【解答】解:并不是任意两个相同的圆和一个曲面就可以组成一个圆柱。 故答案为:错误。 【分析】这个曲面的一边需与底面的圆的周长相等。
三、填空题
12.【答案】12 ;1
【解析】【解答】由题意,假设圆柱和圆锥的体积分别是 /,所以: /。
【分析】由圆柱的体积公式和圆锥的体积公式根据公式推算得出。
13.【答案】9.42
【解析】【解答】:14.13// ????????????? =14.13// ????????????? =9.42(毫升) 【分析】:因为等底等高的圆锥体积是圆柱的/, 所以在装满水圆柱形容器里,放入一个等底等高的圆锥体后,水会溢出和圆锥的体积相等的水,即溢出14.13毫升的/, 由此可得容器内还剩下/的水,由此即可解答。
14.【答案】 157吨
【解析】【解答】3.14×52×3×/×2 =3.14×25×2 =157(吨) 故答案为:157吨
【分析】圆锥的体积=底面积×高×/,由此根据圆锥的体积公式先计算出沙堆的体积,再乘每立方米沙的重量即可求出沙堆的总重量.
15.【答案】30
【解析】【解答】圆锥的体积公式是V= /底面积×高,即 /×18×5=30
【分析】圆锥体积=底面积×高÷3.
16.【答案】0.7536
【解析】【解答】0.628×1.2=0.7536(平方米) 故答案为:0.7536
【分析】根据题意可知,要求制作下水管的铁皮面积,就是求这个圆柱的侧面积,用底面周长×高=圆柱的侧面积,据此列式解答.
17.【答案】 37.68
【解析】【解答】 3.14×4×2+3.l4×( /)2
=25.12+12.56
=37.68(平方厘米)
故答案为:37.68
【分析】由于在池的周围与底面抹上水泥,所以只求它的一个底面和侧面积的和即可,根据圆柱的侧面积公式、圆的面积公式计算。
18.【答案】3
【解析】【解答】9÷3=3(厘米)
【分析】等底等高的圆柱的体积是圆锥体积的3倍,已知体积和底面积都相等,所以圆柱的高是圆锥的高的/,据此解答。
四、计算题
19.【答案】解:表面积: 3.14×4×4+3.14×8×4+3.14×(8÷2)2×2 =50.24+100.48+3.14×16×2 =150.72+100.48 =251.2(平方厘米); 体积: 3.14×(4÷2)2×4+3.14×(8÷2)2×4 =3.14×4×4+3.14×16×4 =50.24+200.96 =251.2(立方厘米); 答:它的表面积是251.2平方厘米,体积是251.2立方厘米。
【解析】【分析】(1)计算零件的表面积,由于上面小圆柱体与下面的大圆柱体的结合面不外露,因此上面的小圆柱体只计算侧面积,下面的大圆柱体计算它的表面积,然后合并起来即可.(2)计算零件的体积就是计算两个圆柱体的体积之和.因此列式解答.
五、解答题
20.【答案】解:3.14×0.5×2.4×100 =3.14×120 =376.8(平方分米) =3.768(平方米)答:能刷墙3.768平方米.
【解析】【分析】圆柱的侧面积=底面周长×高,根据侧面积公式计算出滚动一周的面积,再乘100即可求出能刷墙的面积.
21.【答案】(1)解:
/
(2)解:50.24立方厘米
【解析】【解答】已知底面半径是4厘米,所以这个直角三角形的底是4厘米,高是3厘米,绕3厘米直角边旋转的,体积是/×3.14×42=50.24(立方厘米)
【分析】根据旋转后得到的圆锥的底面半径是4厘米,高是3厘米可知,直角三角形的一条直角边是4厘米,另一条是3厘米,绕着3厘米的直角边旋转即可,根据数据进行作图即可;根据圆锥的体积公式V=/sh进行计算即可得到答案。
六、综合题
22.【答案】(1)解:62.8÷3.14÷2=10(米) 3.14×102+62.8×2 =314+125.6 =439.6(平方米) 答:抹水泥的面积是439.6平方米。 (2)解:3.14×102×(2-0.5) =314×1.95 =612.3(立方米) 答:这时池里的水有612.3立方米。
【解析】【分析】(1)用底面周长除以3.14再除以2求出底面半径,用底面积加上侧面积就是抹水泥部分的面积;(2)用底面积乘水面的高度即可求出水的体积。
七、应用题
23.【答案】解:纸杯的底面半径为:6÷2=3(厘米), 纸杯的容积为:3×32×8 =27×8, =216(立方厘米), 216立方厘米=0.216立方分米=0.216升, 2.2÷0.216≈10(杯); 答:约可以给这种杯子倒10杯水.
【解析】【分析】根据题意,可根据圆柱的体积公式V=底面积×高计算出这个纸杯的容积,然后再用2.2升的水除以杯子的容积即可得到可用倒的杯数,列式解答即可得到答案.解答此题的关键是利用圆柱的体积公式确定纸杯的容积,然后再用一壶水的体积除以杯子的容积即可.
24.【答案】 解:(2÷2)2×3.14x8×5×60÷1000=7.536(升)
【解析】【解答】解:5分钟=300秒 3.14×(2÷2)2×8×300 =3.14×2400 =7536(立方厘米) =7.536(升) 答:5分钟会浪费7.536升水。 【分析】先把5分钟换算成秒,用水管的面积乘每秒流出的长度求出每秒流出水的体积,再乘时间即可求出5分钟流出水的体积,把体积换算成升即可。
一、单选题
1.一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是()立方厘米。
A.? n?????????????????????????????????????????/B.?2n?????????????????????????????????????????/C.?3n?????????????????????????????????????????/D.?4n
2.当一个圆柱的底面________和高相等时,展开这个圆柱的侧面,可以得到一个正方形.(?? )
A.?直径?????????????????????????????????????????/B.?半径?????????????????????????????????????????/C.?周长
3.一个圆柱形纸筒,底面周长和高都是5厘米,把它的侧面沿着高剪开,所得到的侧面展开图是( )
A.?长方形????????????????????????????????????B.?正方形????????????????????????????????????C.?圆????????????????????????????????????D.?梯形
4.一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的(????? )。
A.?2倍???????????????????????????????????????B.?4倍???????????????????????????????????????C.?6倍???????????????????????????????????????D.?8倍
5.一个圆锥体零件,底面直径20厘米,高15厘米.它的体积是(?? )
A.?314立方厘米?????????????????/B.?1570立方厘米?????????????????/C.?4710立方厘米?????????????????/D.?2620立方厘米
6.一个圆锥和一个圆柱的底面积之比是3:2,高之比是1:3,它们的体积比(??? )
A.?1:6?????????????????????????????????????????B.?1:2?????????????????????????????????????????C.?3:2
二、判断题
7.圆柱的表面积用“底面周长×高”来计算。
8.如果一个圆柱体与一个长方体的底面积和高都相等,那么它们的体积也一定相等.
9.等底等高的圆柱体比圆锥体的体积大16立方分米, 这个圆锥的体积是8立方分米。
10.圆锥体的体积是8立方厘米,高是2厘米,底面积是12平方厘米.
11.任意两个相同的圆和一个曲面就可以组成一个圆柱。
三、填空题
12.两个等高的圆柱和圆锥,如果圆柱与圆锥的底面半径这比是2:1,那么圆柱和圆锥的体积最简比是________:________。
13.在一个体积是14.13ml且装满水的圆柱形容器里,放入一个等底等高的圆锥体后.容器里还有水________?ml.
14.一个圆锥形沙堆的底面半径是5米,高是3米.如果每立方米沙重2吨,这堆沙共重________
15.? 一个圆锥底面面积是18厘米,高是5厘米,它的体积是________立方厘米。
16.制作下面圆柱体的物体,至少要用________平方米的铁皮?
/
17.砌一个圆柱形沼气池,底面直径是4米,深是2米。在池的周围与底面抹上水泥,抹水泥部分的面积是________平方米。
18.一个圆柱和一个圆锥,底面积和体积分别相等,圆锥的高是9cm,圆柱的高是________?cm.
四、计算题
19.如图是一种钢制的配件(图中数据单位:cm)请计算它的表面积和体积. /
五、解答题
20.一个刷油漆的滚筒长2.4分米,直径为0.5分米。如果它滚动100周,能刷墙多少平方米?/
21.一个直角三角形,绕它的一条直角边旋转一周,形成了一个底面半径4厘米、高3厘米的圆锥
(1)画出这个直角三角形,并标出是绕哪条直角边旋转的.
/
(2)这个圆锥的体积是多少立方厘米?
六、综合题
22.一个圆柱形游泳池,底面周长为62.8米,深2米。
(1)在池内侧面和池底抹上水泥,抹水泥的面积多少平方米?
(2)水面离池口0.5米,这时池里的水有多少立方米?
七、应用题
23.如图是一种圆柱形纸杯的展开图,一壶2.2升的开水,约可以给这种杯子倒几杯?(π的值取3计算) /
24.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米。一位同学洗完手后忘记关掉水龙头,5分钟会浪费多少升水?( /值取3.14)
答案解析部分
一、单选题
1.【答案】 C
【解析】解答:由题意可知,设圆柱的体积、圆锥的体积分别是 /,由题意可知: /
分析:圆锥的体积公式和圆柱的体积公式。
2.【答案】 C
【解析】【解答】圆柱的侧面展开后如果是一个正方形,说明圆柱的底面周长和高相等. 故答案为:C 【分析】圆柱的侧面展开是一个长方形或正方形,长方形或正方形的一条边的长度与底面周长相等,另一条边的长度与高相等;如果底面周长与高相等时才是正方形.
3.【答案】B
【解析】【解答】解:因为底面周长和高都是5厘米,底面周长与高相等,所以它的侧面展开图是正方形.
故选;B.
【分析】任何圆柱的侧面展开后是一个长方形或正方形,若是长方形,则它的长等于圆柱的底面周长,宽等于圆柱的高;若是正方形,则长与宽相等,即圆柱的底面周长与高相等,据此解答.
4.【答案】 B
【解析】【解答】解:一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的2×2=4倍。 故答案为:B。 【分析】圆锥的体积=/πr2h,当它的高不变,底面半径扩大到原来的2倍后,现在圆锥的体积=/π(r×2)2h=/πr2h×4=原来圆锥的体积×4。
5.【答案】 B
【解析】【解答】3.14×(20÷2)2×15×/ =3.14×100×5 =1570(立方厘米) 故答案为:B
【分析】圆锥的体积=底面积×高×/,由此根据圆锥的体积公式列式计算求出体积即可.
6.【答案】 A
【解析】【解答】解:设它们的高分别为3H、H,
圆柱的体积=2×3H=6H,
圆锥的体积= /×3×H=H,
圆锥与圆柱的体积之比是H:6H=1:6.
故选:A.
【分析】由“一个圆锥和圆柱的底面积之比是3:2”可知把圆柱的底面积看作2份,圆锥的底面积就是3份,设它们的高为H,高之比是1:3,根据圆柱的体积=SH和圆锥的体积= /SH,分别算出体积,最后求出比.
二、判断题
7.【答案】错误
【解析】【解答】圆柱的表面积用底面周长×高+两个底面的面积。 故答案为:错误。
【分析】这道题考查的是圆柱的表面积的知识,圆柱的表面积是圆柱的3个面的面积,即一个侧面的面积和两个底面的面积的和,据此分析判断即可。
8.【答案】正确
【解析】【解答】解:底面积和高分别相等的长方体、圆柱,由于它们的体积都是用底面积×高求得,所以它们的体积也是相等的.
故答案为:正确.
【分析】底面积和高分别相等的长方体、圆柱,它们的体积都是用底面积乘高得来,所以它们的体积也一定相等,依此即可求解.
9.【答案】正确
【解析】【解答】解:16÷2=8(立方分米),原题说法正确。 故答案为:正确。 【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×/, 等底等高的圆柱体积是圆锥体积的3倍,圆柱体积比圆锥大2倍,因此用大的体积除以大的倍数即可求出圆锥的体积。
10.【答案】 正确
【解析】【解答】解:8÷ /÷2
=8×3÷2
=24÷2
=12(平方厘米);
答:它的底面积是12平方厘米.
故答案为:正确.
【分析】根据圆锥的体积公式,v= /sh,已知圆锥体的体积是8立方厘米,高是2厘米,求它的底面积.用体积÷ /÷高;由此列式解答.
11.【答案】 错误
【解析】【解答】解:并不是任意两个相同的圆和一个曲面就可以组成一个圆柱。 故答案为:错误。 【分析】这个曲面的一边需与底面的圆的周长相等。
三、填空题
12.【答案】12 ;1
【解析】【解答】由题意,假设圆柱和圆锥的体积分别是 /,所以: /。
【分析】由圆柱的体积公式和圆锥的体积公式根据公式推算得出。
13.【答案】9.42
【解析】【解答】:14.13// ????????????? =14.13// ????????????? =9.42(毫升) 【分析】:因为等底等高的圆锥体积是圆柱的/, 所以在装满水圆柱形容器里,放入一个等底等高的圆锥体后,水会溢出和圆锥的体积相等的水,即溢出14.13毫升的/, 由此可得容器内还剩下/的水,由此即可解答。
14.【答案】 157吨
【解析】【解答】3.14×52×3×/×2 =3.14×25×2 =157(吨) 故答案为:157吨
【分析】圆锥的体积=底面积×高×/,由此根据圆锥的体积公式先计算出沙堆的体积,再乘每立方米沙的重量即可求出沙堆的总重量.
15.【答案】30
【解析】【解答】圆锥的体积公式是V= /底面积×高,即 /×18×5=30
【分析】圆锥体积=底面积×高÷3.
16.【答案】0.7536
【解析】【解答】0.628×1.2=0.7536(平方米) 故答案为:0.7536
【分析】根据题意可知,要求制作下水管的铁皮面积,就是求这个圆柱的侧面积,用底面周长×高=圆柱的侧面积,据此列式解答.
17.【答案】 37.68
【解析】【解答】 3.14×4×2+3.l4×( /)2
=25.12+12.56
=37.68(平方厘米)
故答案为:37.68
【分析】由于在池的周围与底面抹上水泥,所以只求它的一个底面和侧面积的和即可,根据圆柱的侧面积公式、圆的面积公式计算。
18.【答案】3
【解析】【解答】9÷3=3(厘米)
【分析】等底等高的圆柱的体积是圆锥体积的3倍,已知体积和底面积都相等,所以圆柱的高是圆锥的高的/,据此解答。
四、计算题
19.【答案】解:表面积: 3.14×4×4+3.14×8×4+3.14×(8÷2)2×2 =50.24+100.48+3.14×16×2 =150.72+100.48 =251.2(平方厘米); 体积: 3.14×(4÷2)2×4+3.14×(8÷2)2×4 =3.14×4×4+3.14×16×4 =50.24+200.96 =251.2(立方厘米); 答:它的表面积是251.2平方厘米,体积是251.2立方厘米。
【解析】【分析】(1)计算零件的表面积,由于上面小圆柱体与下面的大圆柱体的结合面不外露,因此上面的小圆柱体只计算侧面积,下面的大圆柱体计算它的表面积,然后合并起来即可.(2)计算零件的体积就是计算两个圆柱体的体积之和.因此列式解答.
五、解答题
20.【答案】解:3.14×0.5×2.4×100 =3.14×120 =376.8(平方分米) =3.768(平方米)答:能刷墙3.768平方米.
【解析】【分析】圆柱的侧面积=底面周长×高,根据侧面积公式计算出滚动一周的面积,再乘100即可求出能刷墙的面积.
21.【答案】(1)解:
/
(2)解:50.24立方厘米
【解析】【解答】已知底面半径是4厘米,所以这个直角三角形的底是4厘米,高是3厘米,绕3厘米直角边旋转的,体积是/×3.14×42=50.24(立方厘米)
【分析】根据旋转后得到的圆锥的底面半径是4厘米,高是3厘米可知,直角三角形的一条直角边是4厘米,另一条是3厘米,绕着3厘米的直角边旋转即可,根据数据进行作图即可;根据圆锥的体积公式V=/sh进行计算即可得到答案。
六、综合题
22.【答案】(1)解:62.8÷3.14÷2=10(米) 3.14×102+62.8×2 =314+125.6 =439.6(平方米) 答:抹水泥的面积是439.6平方米。 (2)解:3.14×102×(2-0.5) =314×1.95 =612.3(立方米) 答:这时池里的水有612.3立方米。
【解析】【分析】(1)用底面周长除以3.14再除以2求出底面半径,用底面积加上侧面积就是抹水泥部分的面积;(2)用底面积乘水面的高度即可求出水的体积。
七、应用题
23.【答案】解:纸杯的底面半径为:6÷2=3(厘米), 纸杯的容积为:3×32×8 =27×8, =216(立方厘米), 216立方厘米=0.216立方分米=0.216升, 2.2÷0.216≈10(杯); 答:约可以给这种杯子倒10杯水.
【解析】【分析】根据题意,可根据圆柱的体积公式V=底面积×高计算出这个纸杯的容积,然后再用2.2升的水除以杯子的容积即可得到可用倒的杯数,列式解答即可得到答案.解答此题的关键是利用圆柱的体积公式确定纸杯的容积,然后再用一壶水的体积除以杯子的容积即可.
24.【答案】 解:(2÷2)2×3.14x8×5×60÷1000=7.536(升)
【解析】【解答】解:5分钟=300秒 3.14×(2÷2)2×8×300 =3.14×2400 =7536(立方厘米) =7.536(升) 答:5分钟会浪费7.536升水。 【分析】先把5分钟换算成秒,用水管的面积乘每秒流出的长度求出每秒流出水的体积,再乘时间即可求出5分钟流出水的体积,把体积换算成升即可。
