四年级下册数学一课一练4.多边形的认识冀教版(含答案)
文档属性
| 名称 | 四年级下册数学一课一练4.多边形的认识冀教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 65.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 11:25:15 | ||
图片预览



文档简介
四年级下册数学一课一练-4.多边形的认识
一、单选题
1.三条边都相等的三角形是(??? )三角形
A.?等腰?????????????????????????????????????????/B.?等边?????????????????????????????????????????/C.?直角
2. 已知一条直线和直线外的A、B两点,以A、B两点和直线上某一点为三角形的三个顶点,能画出一个等腰三角形,如图中的等腰三角形ABC.除此以个最多还能画出符合条件的( )个等腰三角形. /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
3.任何一个三角形都有(????? )高。
A.?一条????????????????????????????????????B.?两条????????????????????????????????????C.?三条????????????????????????????????????D.?无数条
4.∠1和∠2是一个直角三角形中的两个锐角,已知∠1=52°,∠2=(?? )
A.?38°????????????????????????????????????????B.?28°????????????????????????????????????????C.?不能求出
5.平行四边形是易变形图形。(?? )
A.?对? ??????????????????????????????????????????????????????/B.?错
6.在一个三角形中,最大的内角小于90°,这个三角形是(???? )三角形。
A.?锐角?????????????????????????????????????????/B.?钝角?????????????????????????????????????????/C.?直角
二、判断题
7.平行四边形有2种不同的高.
8.有一个角是锐角的三角形,一定是锐角三角形.
9.一个三角形中不可能有两个钝角,但可能有两个直角。
10.三角形按边分为等边三角形和锐角三角形。(??? )
11.有两个角是锐角的三角形一定是锐角三角形。
三、填空题
12.两条边相等的三角形是________。
13.锐角三角形有________个内角是锐角。
14.在一个三角形中,∠1=105°,∠2=25°,那么∠3=________,这是一个________三角形;一个等腰三角形的底角是60°,它的顶角是________,这个三角形也是________三角形.
15.三角形按边分类:________、________、________。
16.请你算出下面三角形的角的度数.
/
∠A=________°
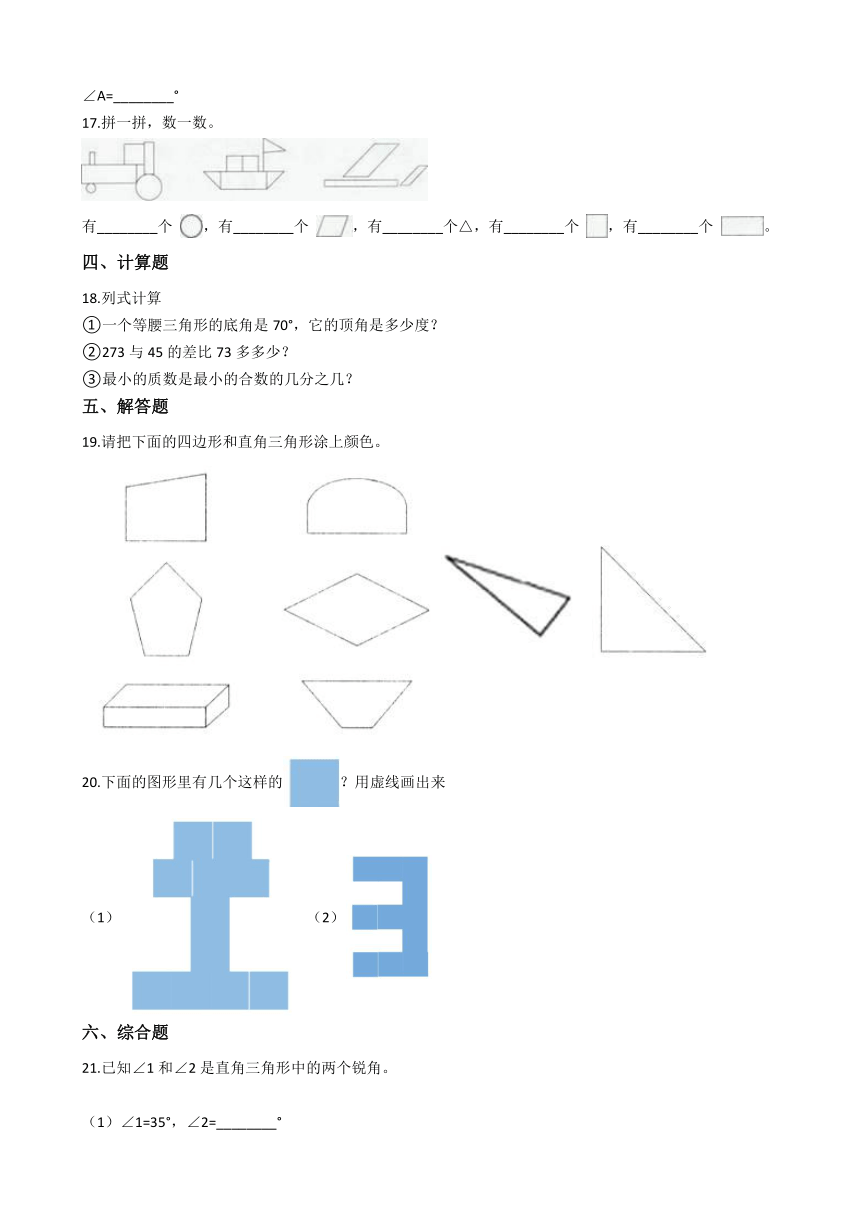
17.拼一拼,数一数。
/
有________个 /,有________个 /,有________个△,有________个 /,有________个 /。
四、计算题
18.列式计算
①一个等腰三角形的底角是70°,它的顶角是多少度?
②273与45的差比73多多少?
③最小的质数是最小的合数的几分之几?
五、解答题
19.请把下面的四边形和直角三角形涂上颜色。
///
20.下面的图形里有几个这样的/?用虚线画出来
(1)/(2)/
六、综合题
21.已知∠1和∠2是直角三角形中的两个锐角。
(1)∠1=35°,∠2=________°
(2)∠1°=28°,∠2=________°
(3)∠1=47°,∠2=________°
七、应用题
22.一个等边三角形的一条边长是10厘米,这个三角形的周长是多少厘米?
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】等边三角形三条边相等 。 【分析】考查了三角形的分类。
2.【答案】 D
【解析】【解答】解:(1)分别是做AB的垂直平分线,与直线的交点是C点,可做等腰三角形;(2)以AB为半径,以A点为圆心画圆,与直线有两个交点,分别是C1、C2 . 这两点均可作为符合条件的C点;(3)同样,以AB为半径,以B点为圆心画圆,与直线交的两个点也符合条件,其中一个就是图上的C点;
答:除此之外还能画出符合条件的4个等腰三角形.
故选:D.
【分析】所做的等腰三角形即可以以AB为腰,也可以以BC为腰,如此考虑就可以找到符合条件的C点,也就能做出符合条件的等腰三角形.
3.【答案】 C
【解析】【解答】任何一个三角形都有三条高。 故答案为:C
【分析】任何一个三角形都有三条高,有的高在三角形内部,有的高在三角形外部。
4.【答案】 A
【解析】【解答】解:∠2=90°-52°=38° 故答案为:A
【分析】三角形内角和是180°,直角三角形两个锐角的度数是90°,由此用90°减去一个锐角的度数即可求出另一个锐角的度数.
5.【答案】 A
【解析】【解答】平行四边形容易变形,具有不稳定性,选A。 【分析】本题考查学生能运用所学知识解决简单的实际问题,而且关键学生思维要灵活。
6.【答案】 A
【解析】【解答】在一个三角形中,最大的内角小于90°,这个三角形是锐角三角形。 故答案为:A
【分析】最大的内角小于90°,其它的两个角也一定小于90°,三个角都是锐角,三个角都是锐角的三角形是锐角三角形。
二、判断题
7.【答案】正确
【解析】【解答】解:如图所示: / 所以平行四边形可以画出两条不同的高,所以原题说法正确。 故答案为:正确 【分析】平行四边形相邻的两条边都可以作为底,两条底边上都能画出高,所以平行四边形有2种不同的高。
8.【答案】错误
【解析】【解答】任何一个三角形都有两个锐角,有三个锐角的三角形一定是锐角三角形,原题说法错误. 故答案为:错误.
【分析】三角形的分类:三个角都是锐角的三角形叫做锐角三角形;有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形,据此解答.
9.【答案】 错误
【解析】【解答】解:若三角形有两个钝角,则这个三角形的内角和必然大于180°,显然不对,所以不可能有两个钝角;两个直角和是:90°+90°=180°,若三角形有两个直角,则这个三角形的内角和也必然大于180°,显然不对,所以也不可能有两个直角。故“可能有两个直角”这个说法是错误的。 故答案为:错误。 【分析】三角形内角和是180°,据此进行解答即可。
10.【答案】错误
【解析】【解答】三角形按边可以分为等边三角形和等腰三角形,
【分析】三角形按边分,可分为两类:不等腰三角形和等腰三角形;等边三角形是等腰三角形的特殊形式,进而解答即可。
故答案为:错误。
11.【答案】 正确
【解析】【解答】略有两个角是锐角的三角形一定是锐角三角形。 故答案为:正确.
【分析】这道题主要考查了三角形的分类.解答此题的关键是根据三角形的分类进行解答.有两个角是锐角的三角形可能是锐角三角形,也可能是钝角三角形.
三、填空题
12.【答案】 等腰三角形
【解析】【解答】等腰三角形两腰相等
【分析】考察了三角形的分类
13.【答案】3
【解析】【解答】锐角三角形的3个角都是锐角。 故答案为:3。【分析】锐角三角形的定义:三个内角都是锐角的三角形是锐角三角形。
14.【答案】 50°;钝角;60°;等边
【解析】【解答】解:∠3=180°﹣105°﹣25°,
=75°﹣25°,
=50°;
这是一个钝角三角形;
180°﹣60°×2,
=180°﹣120°,
=60°;
这个三角形是等边三角形.
故答案为:50°、钝角;60°、等边.
【分析】依据三角形的内角和是180度,两个内角的度数已知,即可求出第三个内角的度数,再据最大角的度数,即可判断这个三角形的类别.因为等腰三角形的两个底角的度数相等,于是依据三角形的内角和定理,即可求出这个等腰三角形的顶角的度数,进而依据角的度数特点,即可判断出这个三角形的类别.解答此题的主要依据是:三角形的内角和定理以及等腰三角形的特点.
15.【答案】 不等边三角形;等腰三角形;等边三角形
【解析】【解答】三角形按边来分类可以分为以下几种:
1、不等边三角形
2、等腰三角形
3、等边三角形
【分析】熟悉三角形按边分类。
16.【答案】 60
【解析】【解答】解:∠A=180°-2×60°=60° 故答案为:60.
【分析】三角形的内角和是180度,用180度减去已知两个角的度数即可得出∠A的度数.
17.【答案】 2 ;2 ;3 ;3 ;5
【解析】
四、计算题
18.【答案】① 它的顶角是40°
②273与45的差比73多15,
③最小的质数是最小的合数的
【解析】【解答】解:①180°﹣70°×2,
=180°﹣140°,
=40°;
答:它的顶角是40°.
②273﹣45﹣73,
=228﹣73,
=155;
答:273与45的差比73多155.
③2÷4= /;
答:最小的质数是最小的合数的 /。
【分析】①在等腰三角形中,2个底角是相等的,这里用180°减去2个70°就是等腰三角形的顶角的度数;
②用273与45的差减去73即可;
③最小的合数是4,最小的质数是2,用2除以4即可。
五、解答题
19.【答案】解:如图:绿色的是四边形,红色的是直角三角形。 /
【解析】【分析】四边形是由四条线段围成的图形,三角形是由三条线段围成的图形,有一个角是直角的三角形是直角三角形,由此判断即可。
20.【答案】(1)解:11个,如图:
/
(2)解:11个,如图:
/
【解析】【分析】每个图形都是由一个小正方形拼成的,根据图形的特征画出小正方形并判断小正方形的个数即可。
六、综合题
21.【答案】(1)90°-35°=55° (2)90°-28°=62° (3)90°-47°=43°
【解析】【分析】直角三角形中两个锐角的和是90度,90度-其中一个锐角度数=另一个锐角度数。
七、应用题
22.【答案】由于等边三角形三边相等,列式可得
10×3=30(cm)
答:三角形的周长是30厘米。
【解析】【解答】由于等边三角形三边相等,列式可得
10×3=30cm
答:三角形的周长是30厘米
【分析】本题主要考查三角形的性质和三角形的周长的计算
一、单选题
1.三条边都相等的三角形是(??? )三角形
A.?等腰?????????????????????????????????????????/B.?等边?????????????????????????????????????????/C.?直角
2. 已知一条直线和直线外的A、B两点,以A、B两点和直线上某一点为三角形的三个顶点,能画出一个等腰三角形,如图中的等腰三角形ABC.除此以个最多还能画出符合条件的( )个等腰三角形. /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
3.任何一个三角形都有(????? )高。
A.?一条????????????????????????????????????B.?两条????????????????????????????????????C.?三条????????????????????????????????????D.?无数条
4.∠1和∠2是一个直角三角形中的两个锐角,已知∠1=52°,∠2=(?? )
A.?38°????????????????????????????????????????B.?28°????????????????????????????????????????C.?不能求出
5.平行四边形是易变形图形。(?? )
A.?对? ??????????????????????????????????????????????????????/B.?错
6.在一个三角形中,最大的内角小于90°,这个三角形是(???? )三角形。
A.?锐角?????????????????????????????????????????/B.?钝角?????????????????????????????????????????/C.?直角
二、判断题
7.平行四边形有2种不同的高.
8.有一个角是锐角的三角形,一定是锐角三角形.
9.一个三角形中不可能有两个钝角,但可能有两个直角。
10.三角形按边分为等边三角形和锐角三角形。(??? )
11.有两个角是锐角的三角形一定是锐角三角形。
三、填空题
12.两条边相等的三角形是________。
13.锐角三角形有________个内角是锐角。
14.在一个三角形中,∠1=105°,∠2=25°,那么∠3=________,这是一个________三角形;一个等腰三角形的底角是60°,它的顶角是________,这个三角形也是________三角形.
15.三角形按边分类:________、________、________。
16.请你算出下面三角形的角的度数.
/
∠A=________°
17.拼一拼,数一数。
/
有________个 /,有________个 /,有________个△,有________个 /,有________个 /。
四、计算题
18.列式计算
①一个等腰三角形的底角是70°,它的顶角是多少度?
②273与45的差比73多多少?
③最小的质数是最小的合数的几分之几?
五、解答题
19.请把下面的四边形和直角三角形涂上颜色。
///
20.下面的图形里有几个这样的/?用虚线画出来
(1)/(2)/
六、综合题
21.已知∠1和∠2是直角三角形中的两个锐角。
(1)∠1=35°,∠2=________°
(2)∠1°=28°,∠2=________°
(3)∠1=47°,∠2=________°
七、应用题
22.一个等边三角形的一条边长是10厘米,这个三角形的周长是多少厘米?
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】等边三角形三条边相等 。 【分析】考查了三角形的分类。
2.【答案】 D
【解析】【解答】解:(1)分别是做AB的垂直平分线,与直线的交点是C点,可做等腰三角形;(2)以AB为半径,以A点为圆心画圆,与直线有两个交点,分别是C1、C2 . 这两点均可作为符合条件的C点;(3)同样,以AB为半径,以B点为圆心画圆,与直线交的两个点也符合条件,其中一个就是图上的C点;
答:除此之外还能画出符合条件的4个等腰三角形.
故选:D.
【分析】所做的等腰三角形即可以以AB为腰,也可以以BC为腰,如此考虑就可以找到符合条件的C点,也就能做出符合条件的等腰三角形.
3.【答案】 C
【解析】【解答】任何一个三角形都有三条高。 故答案为:C
【分析】任何一个三角形都有三条高,有的高在三角形内部,有的高在三角形外部。
4.【答案】 A
【解析】【解答】解:∠2=90°-52°=38° 故答案为:A
【分析】三角形内角和是180°,直角三角形两个锐角的度数是90°,由此用90°减去一个锐角的度数即可求出另一个锐角的度数.
5.【答案】 A
【解析】【解答】平行四边形容易变形,具有不稳定性,选A。 【分析】本题考查学生能运用所学知识解决简单的实际问题,而且关键学生思维要灵活。
6.【答案】 A
【解析】【解答】在一个三角形中,最大的内角小于90°,这个三角形是锐角三角形。 故答案为:A
【分析】最大的内角小于90°,其它的两个角也一定小于90°,三个角都是锐角,三个角都是锐角的三角形是锐角三角形。
二、判断题
7.【答案】正确
【解析】【解答】解:如图所示: / 所以平行四边形可以画出两条不同的高,所以原题说法正确。 故答案为:正确 【分析】平行四边形相邻的两条边都可以作为底,两条底边上都能画出高,所以平行四边形有2种不同的高。
8.【答案】错误
【解析】【解答】任何一个三角形都有两个锐角,有三个锐角的三角形一定是锐角三角形,原题说法错误. 故答案为:错误.
【分析】三角形的分类:三个角都是锐角的三角形叫做锐角三角形;有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形,据此解答.
9.【答案】 错误
【解析】【解答】解:若三角形有两个钝角,则这个三角形的内角和必然大于180°,显然不对,所以不可能有两个钝角;两个直角和是:90°+90°=180°,若三角形有两个直角,则这个三角形的内角和也必然大于180°,显然不对,所以也不可能有两个直角。故“可能有两个直角”这个说法是错误的。 故答案为:错误。 【分析】三角形内角和是180°,据此进行解答即可。
10.【答案】错误
【解析】【解答】三角形按边可以分为等边三角形和等腰三角形,
【分析】三角形按边分,可分为两类:不等腰三角形和等腰三角形;等边三角形是等腰三角形的特殊形式,进而解答即可。
故答案为:错误。
11.【答案】 正确
【解析】【解答】略有两个角是锐角的三角形一定是锐角三角形。 故答案为:正确.
【分析】这道题主要考查了三角形的分类.解答此题的关键是根据三角形的分类进行解答.有两个角是锐角的三角形可能是锐角三角形,也可能是钝角三角形.
三、填空题
12.【答案】 等腰三角形
【解析】【解答】等腰三角形两腰相等
【分析】考察了三角形的分类
13.【答案】3
【解析】【解答】锐角三角形的3个角都是锐角。 故答案为:3。【分析】锐角三角形的定义:三个内角都是锐角的三角形是锐角三角形。
14.【答案】 50°;钝角;60°;等边
【解析】【解答】解:∠3=180°﹣105°﹣25°,
=75°﹣25°,
=50°;
这是一个钝角三角形;
180°﹣60°×2,
=180°﹣120°,
=60°;
这个三角形是等边三角形.
故答案为:50°、钝角;60°、等边.
【分析】依据三角形的内角和是180度,两个内角的度数已知,即可求出第三个内角的度数,再据最大角的度数,即可判断这个三角形的类别.因为等腰三角形的两个底角的度数相等,于是依据三角形的内角和定理,即可求出这个等腰三角形的顶角的度数,进而依据角的度数特点,即可判断出这个三角形的类别.解答此题的主要依据是:三角形的内角和定理以及等腰三角形的特点.
15.【答案】 不等边三角形;等腰三角形;等边三角形
【解析】【解答】三角形按边来分类可以分为以下几种:
1、不等边三角形
2、等腰三角形
3、等边三角形
【分析】熟悉三角形按边分类。
16.【答案】 60
【解析】【解答】解:∠A=180°-2×60°=60° 故答案为:60.
【分析】三角形的内角和是180度,用180度减去已知两个角的度数即可得出∠A的度数.
17.【答案】 2 ;2 ;3 ;3 ;5
【解析】
四、计算题
18.【答案】① 它的顶角是40°
②273与45的差比73多15,
③最小的质数是最小的合数的
【解析】【解答】解:①180°﹣70°×2,
=180°﹣140°,
=40°;
答:它的顶角是40°.
②273﹣45﹣73,
=228﹣73,
=155;
答:273与45的差比73多155.
③2÷4= /;
答:最小的质数是最小的合数的 /。
【分析】①在等腰三角形中,2个底角是相等的,这里用180°减去2个70°就是等腰三角形的顶角的度数;
②用273与45的差减去73即可;
③最小的合数是4,最小的质数是2,用2除以4即可。
五、解答题
19.【答案】解:如图:绿色的是四边形,红色的是直角三角形。 /
【解析】【分析】四边形是由四条线段围成的图形,三角形是由三条线段围成的图形,有一个角是直角的三角形是直角三角形,由此判断即可。
20.【答案】(1)解:11个,如图:
/
(2)解:11个,如图:
/
【解析】【分析】每个图形都是由一个小正方形拼成的,根据图形的特征画出小正方形并判断小正方形的个数即可。
六、综合题
21.【答案】(1)90°-35°=55° (2)90°-28°=62° (3)90°-47°=43°
【解析】【分析】直角三角形中两个锐角的和是90度,90度-其中一个锐角度数=另一个锐角度数。
七、应用题
22.【答案】由于等边三角形三边相等,列式可得
10×3=30(cm)
答:三角形的周长是30厘米。
【解析】【解答】由于等边三角形三边相等,列式可得
10×3=30cm
答:三角形的周长是30厘米
【分析】本题主要考查三角形的性质和三角形的周长的计算
