高中数学北师大必修5第三章不等式4.1二元一次不等式(组)与平面区域教学课件 共19张
文档属性
| 名称 | 高中数学北师大必修5第三章不等式4.1二元一次不等式(组)与平面区域教学课件 共19张 |

|
|
| 格式 | zip | ||
| 文件大小 | 745.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-10 08:05:42 | ||
图片预览





文档简介
课件19张PPT。欢迎同学们和我一起发现与探索生活中的数学引入: 为装点元旦晚会会场,本班计划用最多100元钱购买单价分别为5元和10元的小彩球、大彩球,根据需要,小球数不少于5个,大球数不少于3个,请你给出几种不同的购买方案? 问题:应该用什么不等式模型来刻画呢? 二元一次不等式(组)
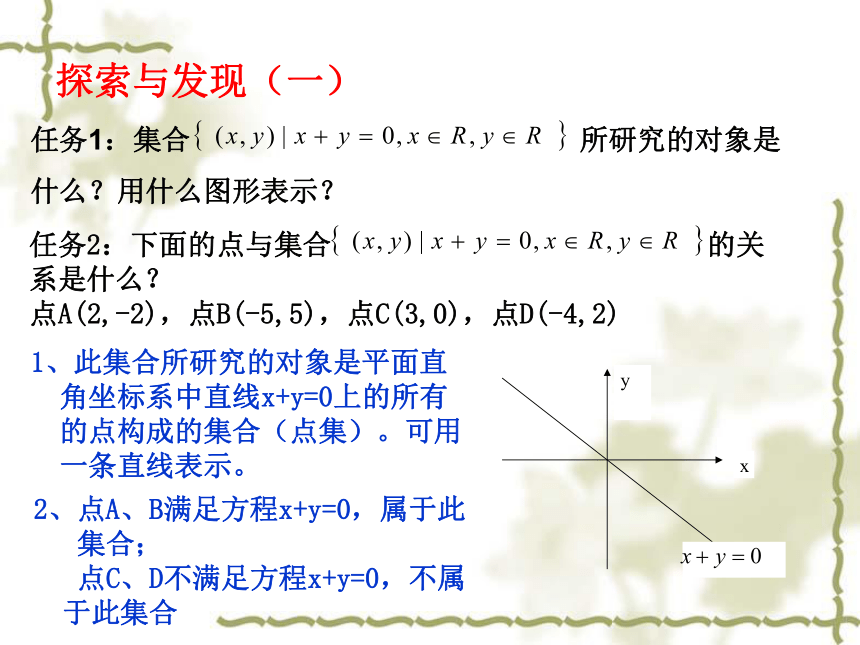
与平面区域——二元一次不等式(组)定义(1)二元一次不等式: (2)二元一次不等式组: 由几个二元一次不等式组成的不等式组; (3)二元一次不等式(组)的解集: 满足二元一次不等式(组)的有序实数对(x,y)构成的集合;(4)二元一次不等式(组)的解集可以看成是直角坐标系内的点构成的集合。 概念形成1、此集合所研究的对象是平面直
角坐标系中直线x+y=0上的所有
的点构成的集合(点集)。可用
一条直线表示。探索与发现(一)2、点A、B满足方程x+y=0,属于此
集合;
点C、D不满足方程x+y=0,不属
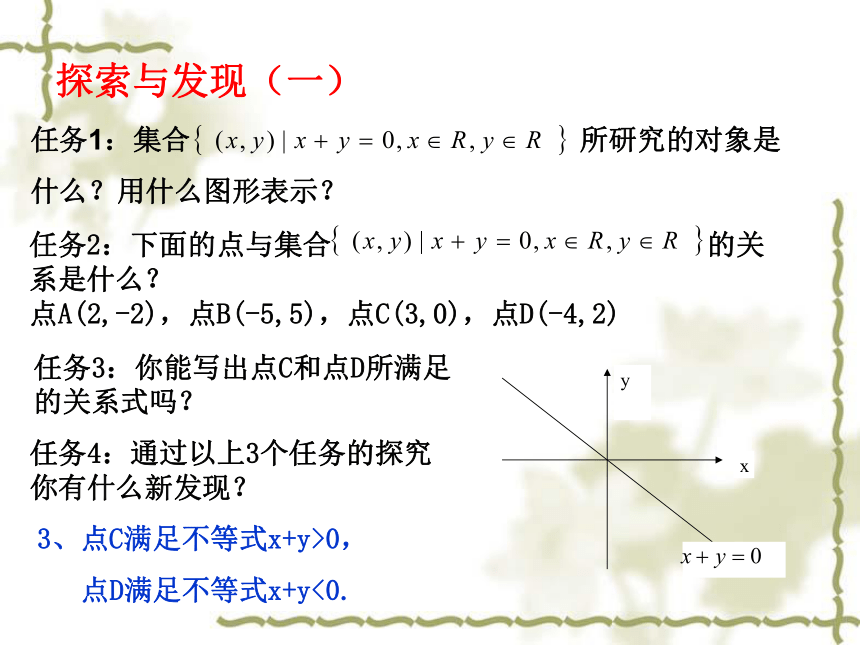
于此集合探索与发现(一)任务3:你能写出点C和点D所满足的关系式吗?3、点C满足不等式x+y>0,
点D满足不等式x+y<0.任务4:通过以上3个任务的探究你有什么新发现?方法提炼(一)探索与发现(二)任务5:你能否发现:
直线x+y=0右上方的所有点满足的关系式是什么?
直线x+y=0左下方的所有点满足的关系式是什么?
你能给出合理的解释吗? 问题:方程x+y=0的图像是一条直线,那么不等式x+y>0和x+y<0如何用图形表示呢?x+y>0x+y<0探索与发现(二)x+y>0x+y<0任务6:试确定不等式所表示的平面区域。解:建立平面直角坐标系,将坐标原点(0,0)代入不等式左边可得,探索与发现(二)任务7:试确定不等式所表示的平面区域。解:建立平面直角坐标系,探索与发现(二) 画Ax+By+C>0(或<0)的平面区域时,边界直线画成虚线表示区域不包括边界;
画Ax+By+C≥0 (或≤0)的平面区域时,边界直线画成实线表示区域包括边界.方法提炼(二)二元一次不等式表示平面区域的步骤:简单来说:直线定界 ,特殊点定域。第一步:画不等式的边界直线Ax+By+C=0;第二步:取一特殊点代入Ax+By+C,根据值的正负确定不等式的平面区域,用阴影表示出所求平面区域。(直线定界)(特殊点定域)练习:作出下列不等式表示的平面区域夯实基础直线定界(虚实分明) ,
特殊点定域(常取原点) 。能力提升不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分。 步骤:直线定界(虚实分明) ,特殊点定域(常取原点) 。 为装点元旦晚会会场,本班计划用最多100元钱购买单价分别为5元和10元的小彩球、大彩球,根据需要,大球数不少于3个,小球数不少于5个,请你给出几种不同的购买方案?回归生活解:设购买小球数x个,大球数y个 购买方式应满足的条件:x1、能从实际情境中抽象出二元一次不等式(组),建立了不
等关系的数学模型。4、明白了二元一次不等式组表示的平面区域是各二元一次不
等式所表示的平面区域的公共部分。 3、建立了数(二元一次不等式)形(平面区域)结合的思想。直线定界,特殊点定域。归纳小结请同学们归纳一下通过本节课的学习收获了什么?2、掌握了用平面区域表示不等式的方法:课堂检测:1、不等式3x + 2y – 6 ≤0表示的平面区域是( )D2、不等式组表示的平面区域是( )B3、确定m的取值范围使点(1,2)和点(1,1)在直线y-3x-m=0的
异侧。分析:只要满足点(1,2)和点(1,1)分别代入y-3x-m得到的符号相反解:由题意可知 (-1-m)(-2-m)<0,解得-2A组 3、4、5作业:
角坐标系中直线x+y=0上的所有
的点构成的集合(点集)。可用
一条直线表示。探索与发现(一)2、点A、B满足方程x+y=0,属于此
集合;
点C、D不满足方程x+y=0,不属
于此集合探索与发现(一)任务3:你能写出点C和点D所满足的关系式吗?3、点C满足不等式x+y>0,
点D满足不等式x+y<0.任务4:通过以上3个任务的探究你有什么新发现?方法提炼(一)探索与发现(二)任务5:你能否发现:
直线x+y=0右上方的所有点满足的关系式是什么?
直线x+y=0左下方的所有点满足的关系式是什么?
你能给出合理的解释吗? 问题:方程x+y=0的图像是一条直线,那么不等式x+y>0和x+y<0如何用图形表示呢?x+y>0x+y<0探索与发现(二)x+y>0x+y<0任务6:试确定不等式所表示的平面区域。解:建立平面直角坐标系,将坐标原点(0,0)代入不等式左边可得,探索与发现(二)任务7:试确定不等式所表示的平面区域。解:建立平面直角坐标系,探索与发现(二) 画Ax+By+C>0(或<0)的平面区域时,边界直线画成虚线表示区域不包括边界;
画Ax+By+C≥0 (或≤0)的平面区域时,边界直线画成实线表示区域包括边界.方法提炼(二)二元一次不等式表示平面区域的步骤:简单来说:直线定界 ,特殊点定域。第一步:画不等式的边界直线Ax+By+C=0;第二步:取一特殊点代入Ax+By+C,根据值的正负确定不等式的平面区域,用阴影表示出所求平面区域。(直线定界)(特殊点定域)练习:作出下列不等式表示的平面区域夯实基础直线定界(虚实分明) ,
特殊点定域(常取原点) 。能力提升不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分。 步骤:直线定界(虚实分明) ,特殊点定域(常取原点) 。 为装点元旦晚会会场,本班计划用最多100元钱购买单价分别为5元和10元的小彩球、大彩球,根据需要,大球数不少于3个,小球数不少于5个,请你给出几种不同的购买方案?回归生活解:设购买小球数x个,大球数y个 购买方式应满足的条件:x1、能从实际情境中抽象出二元一次不等式(组),建立了不
等关系的数学模型。4、明白了二元一次不等式组表示的平面区域是各二元一次不
等式所表示的平面区域的公共部分。 3、建立了数(二元一次不等式)形(平面区域)结合的思想。直线定界,特殊点定域。归纳小结请同学们归纳一下通过本节课的学习收获了什么?2、掌握了用平面区域表示不等式的方法:课堂检测:1、不等式3x + 2y – 6 ≤0表示的平面区域是( )D2、不等式组表示的平面区域是( )B3、确定m的取值范围使点(1,2)和点(1,1)在直线y-3x-m=0的
异侧。分析:只要满足点(1,2)和点(1,1)分别代入y-3x-m得到的符号相反解:由题意可知 (-1-m)(-2-m)<0,解得-2
